Для возможности изучения эффекта действия на тело сил, как угодно расположенных в пространстве, вводится понятие момента силы относительно оси.

Рис.6.4
Пусть заданы ось n исила  , приложенная к телу в точке А. Для определения момента силы относительно оси n, проведем плоскость П, перпендикулярную к заданной оси n и обозначим точку пересечения плоскости с осью буквой O (рис.6.4).
, приложенная к телу в точке А. Для определения момента силы относительно оси n, проведем плоскость П, перпендикулярную к заданной оси n и обозначим точку пересечения плоскости с осью буквой O (рис.6.4).
Пользуясь правилом треугольника сил, разложим заданную силу  на две составляющие, одна из которых
на две составляющие, одна из которых  параллельна плоскости П, а другая
параллельна плоскости П, а другая  параллельна оси n, т.е. перпендикулярна указанной плоскости. Из рисунка 6.4 видно, что составляющая
параллельна оси n, т.е. перпендикулярна указанной плоскости. Из рисунка 6.4 видно, что составляющая  равна проекции заданной силы на плоскость:
равна проекции заданной силы на плоскость:  . Очевидно, что момент заданной силы
. Очевидно, что момент заданной силы  относительно оси n -, характеризующий эффект её вращательного воздействия, равен сумме моментов составляющих сил относительно той же оси. Но составляющая
относительно оси n -, характеризующий эффект её вращательного воздействия, равен сумме моментов составляющих сил относительно той же оси. Но составляющая  параллельна оси n и, следовательно, не может осуществить поворот тела относительно этой оси (т.е. её момент относительно оси n равен нулю), а момент составляющей
параллельна оси n и, следовательно, не может осуществить поворот тела относительно этой оси (т.е. её момент относительно оси n равен нулю), а момент составляющей  относительно оси n равен моменту силы
относительно оси n равен моменту силы  относительно точки пересечения этой оси с плоскостью.
относительно точки пересечения этой оси с плоскостью.
Таким образом, момент силы относительно некоторой оси равен моменту её проекции на плоскость перпендикулярную к этой оси, относительно точки пересечения оси с плоскостью, т.е:
 (6.8)
(6.8)
Момент силы относительно оси принимается положительным, если её проекция на плоскость перпендикулярную к оси стремится повернуть тело против часовой стрелке, если действие силы рассматривать со стороны положительного направления оси.
Возможны три частных случая расположения силы и оси в пространстве:
I. Сила  действует в плоскости, перпендикулярной к оси n (рис.6.5). В этом случае момент заданной силы относительно оси п равен моменту той же силы относительно точки пересечения плоскости с осью, т.е.
действует в плоскости, перпендикулярной к оси n (рис.6.5). В этом случае момент заданной силы относительно оси п равен моменту той же силы относительно точки пересечения плоскости с осью, т.е. 

Рис.6.5
2. Сила  параллельна оси n (рис.62). Момент этой силы относительно заданной оси равен нулю, так как равна нулю её проекция на плоскость П, перпендикулярную к оси п.
параллельна оси n (рис.62). Момент этой силы относительно заданной оси равен нулю, так как равна нулю её проекция на плоскость П, перпендикулярную к оси п.
3. Линия действия силы  пересекает ось n в точке С. В
пересекает ось n в точке С. В
этом случае линия действия проекции заданной силы на плоскость П пересечет ось n в точке О (рис.62). Поэтому момент силы  относительно оси n равен нулю.
относительно оси n равен нулю.
Приведение пространственной системы произвольно
Расположенных сил к заданному центру.
Условия равновесия
Согласно теореме Пуансо, всякая сила может быть перенесена параллельно её линии действия в любую точку тела. При этом, действие заданной силы заменяется действием такой же силы, приложенной в центре приведения и действием присоединенной пары сил, момент которой равен моменту заданной силы относительно центра приведения.
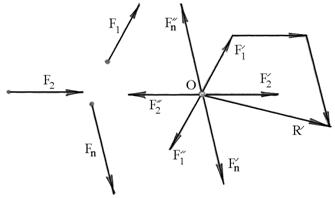
Рис.6.6
Пусть твердое тело загружено силами  ,
,  ,
,  ,…,
,…, 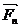 , не лежащими в одной плоскости (рис.6.6). Возьмем точку О тела в качестве центра приведения и приложим в ней по две взаимно уравновешенные силы
, не лежащими в одной плоскости (рис.6.6). Возьмем точку О тела в качестве центра приведения и приложим в ней по две взаимно уравновешенные силы  и
и  ,
, 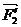 и
и  ,...
,...  и
и 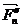 соответственно равные и параллельные заданным силам. В результате получаем пространственную систему сходящихся сил
соответственно равные и параллельные заданным силам. В результате получаем пространственную систему сходящихся сил  ,
, 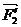 ,…,
,…,  - и пространственную систему пар (
- и пространственную систему пар ( ,
,  ), (
), ( ,
,  ),...,(
),...,(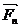 ,
, 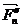 ).
).
Равнодействующая  сходящихся сил
сходящихся сил  ,
, 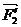 ,…,
,…,  равна их геометрической сумме и называется главным вектором заданных сил.
равна их геометрической сумме и называется главным вектором заданных сил.
 =
=  +
+ 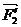 + …+
+ …+ 
Напомним, что главный вектор и равнодействующая произвольной системы сил имеют одинаковые модули и направления, параллельны между собой, но их линии действия не совпадают.
Модуль главного вектора определяется по формуле (4.7), а его проекции на координатные оси по формулам (4.8).
Приведенные пары ( ,
,  ), (
), ( ,
,  ),...,(
),...,(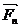 ,
, 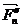 ) расположены в разных плоскостях и их действие на тело можно заменить действием одной результирующей пары, расположенной в новой плоскости. Момент этой пары
) расположены в разных плоскостях и их действие на тело можно заменить действием одной результирующей пары, расположенной в новой плоскости. Момент этой пары  называется главным моментом заданной системы сил относительно выбранного центра.
называется главным моментом заданной системы сил относительно выбранного центра.
Если воспользоваться понятием момента силы как вектора, имеющего в пространстве три взаимно перпендикулярные составляющие, то модуль главного момента определится выражением:
 (6.9)
(6.9)
где 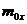 ,
,  ,
,  - проекции вектора главного момента на координатные оси x, y и z соответственно.
- проекции вектора главного момента на координатные оси x, y и z соответственно.
Опуская доказательство, укажем, что проекция вектора главного момента на любую ось равна алгебраической сумме моментов всех заданных сил относительно той же оси, т.е:
 ,
,  ,
,  (6.10)
(6.10)
Таким образом, произвольная система сил в пространстве приводится к главному вектору, равному геометрической сумме заданных сил и приложенному в центре приведения и к главному моменту этих сил относительно центра приведения.
Для равновесия системы сил, произвольно расположенных в пространстве необходимо, чтобы главный вектор и главный момент этой системы были одновременно равными нулю, т.е:
 = 0 и
= 0 и  (6.11)
(6.11)
Используя формулы (6.5) и (6.9) с учетом зависимостей (6.6) и (6.10), устанавливаем, что равенства (6.11) возможны при выполнении следующих шести условий:
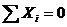 ,
,  ,
, 
 ,
,  ,
,  (6.12)
(6.12)
Следовательно, система произвольно расположенных сил в пространстве находится в равновесии в том случае, когда одновременно равны нулю алгебраические суммы проекций всех сил на три взаимно перпендикулярные оси и алгебраические суммы моментов всех сил относительно тех же осей.
Из условий (6.12) вытекают уравнения равновесия, решение которых дает возможность вычислить шесть неизвестных параметров системы сил, под действием которой тело находится в равновесии. Обычно в задачах статики неизвестными являются величины и направления реакций опорных связей. Если же система сил имеет более шести неизвестных параметров, то задача является статически неопределимой. Решение таких задач рассматривается в статике сооружений.




