Содержание этой аксиомы поясним на примере. Пусть задано твердое тело (рис.1.4), к которому в точках А и В соответственно приложены силы 
и 
, действующие вдоль прямой АВ. Если модули этих сил равны, т.е. 
= 
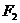, а направления их противоположны, то данное тело будет находиться в равновесии (покое). При не соблюдении хотя бы одного из указанных условий равновесие тела нарушится. Две равные и противоположно направленные силы составляют простейшую уравновешенную систему сил.
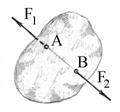
Рис.1.4
Аксиома II. Равновесие твердого тела не нарушится, если к заданным силам присоединить, или от них отобрать систему уравновешенных сил.
Эта аксиома очевидна в виду того, что любая система уравновешенных сил эквивалентна нулю и не может, следовательно, изменить состояние равновесия твердого тела.
Из рассмотренных двух аксиом вытекает важное для теории и практики следствие о переносе точки приложения силы вдоль линии её действия. Пусть тело, представленное на рис.1.5, находится в равновесии, или движется равномерно и прямолинейно под действием некоторой системы сил: , 
, ,…, 
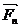. Продолжим линию действия одной из сил, например , и приложим в некоторой точке В этой линии две равные и противоположно направленные силы 
и 
, которые, согласно аксиоме I, не изменяют состояние тела. Положим, что модули этих сил равны модулю силы , т.е.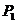 
= 
= 
.
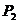В этом случае силы и равные по величине и действующие вдоль общей прямой в противоположные стороны, взаимно уравновешиваются.
Согласно аксиоме II они могут быть удалены без нарушения состояния равновесия или движения этого тела.
Рис.1.5
В результате, вместо силы на тело будет действовать статически равная ей сила , приложенная в произвольной точке В, взятой на линии действия силы . Приведенное рассуждение справедливо по отношению к любой силе заданной системы.
Следствие из аксиомынужденные колебания.ю свободы. Свободные и вбающих моментов, подбор сечений и определение перемещений.: Состояние твердого тела не нарушится от переноса точки приложения любой силы вдоль её линии действия в новое произвольное положение.
Аксиома III. Равнодействующая двух сил, приложенных к телу в одной точке равна диагонали параллелограмма, построенного на этих силах. Точка приложения равнодействующей совпадает с точкой приложения заданных сил.
Рис.1.6
На рис.1.6 показано действие на тело двух сил и , приложенных в точке А. Диагональ АС параллелограмма, построенного на этих силах, будет являться их равнодействующей 
.
На основании аксиомы III осуществляется геометрическое сложение двух сил, а также произвольного числа сил, расположенных в пространстве или на плоскости.
