Изучаемые в механике величины разделяют на два класса: скалярные и векторные. Скалярные величины полностью характеризуются численным их значением. К таким величинам относятся объём, площадь, моменты инерции и др. Векторные величины характеризуются численным значением (модулем), точкой приложения, линией действия и направлением в пространстве или на плоскости. Сила, скорость, ускорение являются векторными величинами.
Графически векторная величина изображается отрезком прямой АВ, направление которого изображается стрелкой (рис.1.1). Длина отрезка в выбранном масштабе определяет численную величину или модуль вектора. Прямая линия, совпадающая с вектором и продолженная неограниченно, называется линией действия вектора. Точка приложения вектора к телу может совпадать с его началом (точкой А) или с его концом (точкой В).
Рис.1.1
Остановимся более подробно на характеристике вектора силы.
Он характеризует результат механического взаимодействия материальных тел. Вектор силы обозначают в тексте одной латинской буквой со стрелкой наверху (например 
), либо двумя буквами со стрелкой над ними (например, 
). Те же буквы без верхней стрелки служат для обозначения модуля силы. Например, 
есть модуль силы . На рисунках нет необходимости силу обозначать символом вектора, т.е. символом , так как она уже представлена вектором и поэтому достаточно указать её модуль (см. рис.1.1).
За единицу силы в Международной системе СИ принимается сила, которая массе в I кг сообщает ускорение I 
. Эта величина называется ньютон (сокращенно - I Н).
В технической системе единиц МКГСС, которая часто используется в механике наряду с системой СИ, за единицу силы принимают килограмм силы (сокращенно - I кгс). Эта величина равна весу одного кубического дециметра воды при температуре 4°С на уровне моря и на широте 45°.
В таблице I приложения приведены основные и производные единицы измерения механических величин в двух системах и перевод их из одной системы в другую.
Величина силы взаимодействия между двумя телами может быть измерена опытным путем при помощи динамометров (силомеров).
Совокупность сил, действующих одновременно на рассматриваемое тело, называется системой сил. Силы одной системы называют составляющими или компонентами. Если под действием системы сил тело находится в равновесии, то такая система сил является уравновешенной или эквивалентной нулю.
Две системы сил называют статически эквивалентными, если их взаимная замена не приводит к изменению состояния равновесия или равномерного и прямолинейного движения тела. Это понятие позволяет упрощать решение задач статики путем замены сложной системы сил более простой, но ей эквивалентной.
Важнейшим принципом, которому подчинены силы любой системы, является принцип независимого их действия. Он формулируется следующим образом. Действие каждой силы данной системы не зависит от действия других сил. Иными словами, результат действия системы сил на тело не зависит от порядка их приложения, а определяется конечным состоянием загружения тела. Этот принцип широко используется при сложении сил, т.е. при определении их равнодействующей.
Равнодействующей системы сил называют такую силу, результат действия которой полностью совпадает с результатом действия заданной системы сил.
Необходимо помнить, что не всякая система сил может быть эквивалентна равнодействующей. При изучении действия на тело плоской и пространственной системы сил, этот вопрос будет рассмотрен подробно. Если система действующих на тело сил может быть приведена в состояние равновесия (покоя) путем приложения к телу ещё одной силы, то последняя называется уравновешивающей силой.
Легко установить, что равнодействующая и уравновешивающая силы равны по величине и действуют вдоль общей прямой в противоположные стороны. На рис.1.2 показана систем а сил 
, , ,…, 
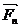, приводящаяся к равнодействующей 
, линия действия которой проходит через точку А. Сила 
, приложенная в точке А, равная по модулю силе и направленная противоположно ей, является уравновешивающей силой для данной системы.
Рис.1.2
Если система сил не приводится к одной равнодействующей, то она не может быть уравновешена одной силой. Для этого требуется приложить к телу новую систему сил, которая называется уравновешивающей системой.
Задача установления условий, при которых твердое тело под действием заданных сил находится в равновесии, является основной задачей статики. Такие условия позволяют определить величины и направления уравновешивающих сил или систем.
1.2. Силы внутренние и внешние.
Любое материальное тело конечных размеров можно представить системой бесконечно большого числа материальных точек. Силы, с которыми указанные точки действуют одна на другую, называются внутренними силами. По своей природе внутренние силы являются уравновешенными и существуют в любом изолированном или связанном теле. Определение и исследование внутренних сил составляет специальную задачу, рассматриваемую в раздел II (основы сопротивления материалов) и в разделе III (основы строительной механики).
Кроме внутренних сил на материальные точки тела действуют внешние силы, являющиеся результатом взаимодействия рассматриваемого тела с другими телами. Внешние силы разделяются на поверхностные и объёмные (массовые).
Поверхностные силы, как правило, являются распределенными по некоторым площадкам тела, но при решении задач механики твердого тела они могут быть заменены более простыми сосредоточенными силами. На рис.1.3,а показано возможное нагружение тела распределенной нагрузкой q в реальных условиях, а на рис.1.3,6 показано нагружение этого же тела сосредоточенной силой , эквивалентной по своему действию распределенной нагрузке q.
Рис.1.3
Аксиомы статики.
В результате постоянного изучения явлений, происходящих в окружающем мире, устанавливаются истины, которые в силу своей очевидности не требуют доказательства. Такие истины называют аксиомами. Впервые система аксиом механики была установлена Ньютоном и отражала истины, свойственные движению твердого тела под действием приложенных к нему сил. Аксиомы статики, достаточные для обоснования частного случая движения тела, т.е. его равновесия, являются следствием общих Ньютоновских аксиом.
