Цель работы: Изучение и экспериментальное исследование явления резонанса напряжений.
Основные теоретические сведения
Резонансом называется такой режим электрической цепи, при которой входной ток совпадает по фазе с входным напряжением, несмотря на наличие в цепи реактивных элементов.
Резонансный режим наступает тогда, когда частота внешних воздействий на систему равна собственной частоте системы,
ω=2π f = ω0= 2π f 0 (4.1)
т.е. частоте преобразования энергии внутри системы из одной формы в другую (энергия магнитного поля в энергию электрического поля и наоборот). Резонанс, таким образом, возникает при наличии в цепи индуктивности и емкости.
Одна из ценных особенностей резонансов - это значительное увеличение напряжений или токов при весьма экономичном использовании электрической энергии.
Резонанса в электрической цепи можно достичь, изменяя либо частоту источника питания, либо индуктивность, либо емкость.
Цепь, находящаяся в резонансном режиме, характеризуется следующим:
1. входные реактивные сопротивления или проводимости равны нулю:
x вх=0;  b вх=0;
b вх=0;
2. угол сдвига фаз между входным током и выходным напряжением равен нулю, а коэффициент мощности максимален.
φвх=0; cos φвх= I;
3. входная мощность чисто активная:
S вх= P вх+ jQ вх= P вх;
Резонанс напряжений
Резонанс при последовательном соединении индуктивности и емкости, при взаимной компенсации реактивных составляющих напряжения U вх, называют резонансом напряжений.
Если к цепи, изображенной на рис. 4-1, приложено переменное синусоидальное напряжение
 u вх=√2 U вх sin ω t, (4.2)
u вх=√2 U вх sin ω t, (4.2)
то ток равен
 iвх=√2 sin (ω t + φ) U вх/ Z вх=√2 sin (ω t + φ) U вх/√ R 2+ x вх2=√2 I вх sin (ω t + φ), (4.3)
iвх=√2 sin (ω t + φ) U вх/ Z вх=√2 sin (ω t + φ) U вх/√ R 2+ x вх2=√2 I вх sin (ω t + φ), (4.3)
где
φ= arctg (x вх/ R); x вх= x L- x C=ω L- 1 / (ω C).
Из приведенного выражения (4.3) видно, что ток i вх будет совпадать с приложенным напряжением при условии x вх = 0 или
ω L =1 / (ω C), (4.4)
т.е. x L= x C.
Таким образом, при резонансе напряжений входное реактивное сопротивление x вх равно нулю, а полное сопротивление z вх имеет наименьшее значение, поэтому ток в цепи максимален.
При резонансе напряжений реактивные составляющие напряжения U вх равны между собой:
U L= U C.
и могут во много раз превышать напряжение, приложенное к цепи, что характеризуется добротностью контура:
Q вх= U C/ U вх= U L/ U вх=ρ/ R = (200–500), (4.5)
где ρ - волновое или характеристическое сопротивление контура.
 ρ=√ L /C (4.6)
ρ=√ L /C (4.6)
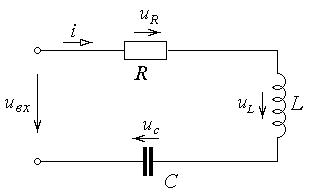
Рис. 4-1. Схема замещения последовательной цепи
Векторная диаграмма резонанса напряжений в цепи (рис. 4-1) имеет вид:
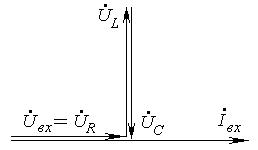
Рис. 4-2. Векторная диаграмма резонанса напряжений
Нерезонансные режимы
Режимы вне резонанса можно получить, если вывести систему из резонанса, т.е. нарушить условие (4.1), изменяя собственную частоту контура с помощью индуктивности L при постоянной емкости C, или изменяя емкость C при постоянной индуктивности L. В результате этой операции можно получить частотные характеристики (рис. 4-3 и рис. 4-4).
Следует отметить, что острота всех частотных характеристик зависят от добротности цепи Qg. Чем выше Qg, тем более острыми получаются пики всех кривых и поэтому резко возрастают избирательные свойства цепи.
Изменяя величину емкости конденсатора при постоянной индуктивности можно получить графики функциональных зависимостей в последовательной цепи (рис. 4-5) и построить соответствующие векторные диаграммы (рис. 4-6).
Для схемы (рис. 4-1) на основании векторных диаграмм для нерезонансных режимов (рис. 4-6) можно построить треугольник напряжений для всей цепи (рис. 4-7, a) и соответствующий треугольник сопротивлений (рис. 4-7. б).
Из треугольника напряжений (рис. 4-7,а) следует:
cos φвх= U a/ U вх (4.7)
где U a- активная составляющая входного напряжения.
Из треугольника сопротивлений также можно определить величину коэффициента мощности:
cos φвх= R / Z вх. (4.8)
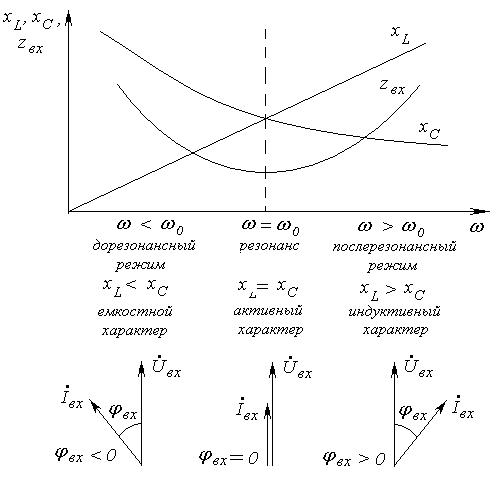
Рис. 4-3. Частотные характеристики сопротивлений последовательной цепи
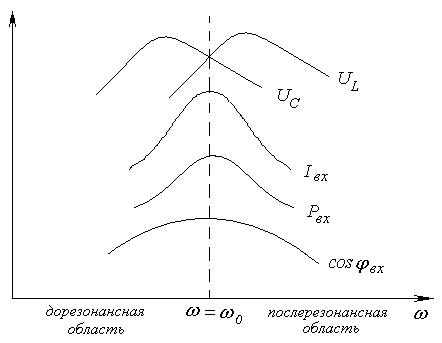
Рис. 4-4. Частотные характеристики тока, напряжения, мощности и коэффициента мощности последовательной цепи

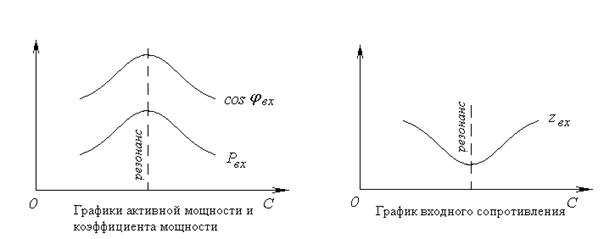
Рис. 4-5. График функциональных зависимостей в последовательной цепи
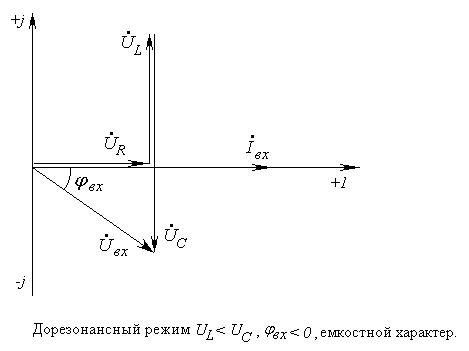
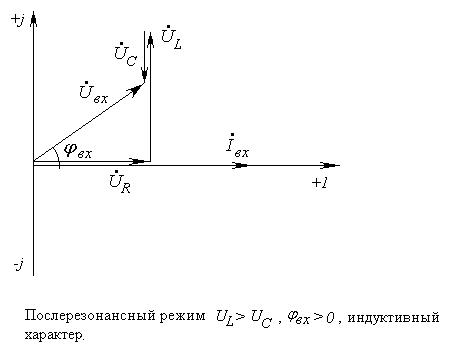
Рис. 4-6. Векторные диаграммы последовательной цепи для нерезонансных режимов

Рис. 4-7. Треугольник напряжений (а) и треугольник сопротивлений (б) последовательной цепи
Перечень оборудования
1. Источники переменного напряжения 36 В, 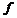 =50 Гц.
=50 Гц.
2. Катушка индуктивности с ферромагнитным сердечником с подмагничиванием (подмагничивание постоянным током уменьшает эквивалентную индуктивность катушка). Цепь подмагничивания включается тумблерами.
3. Батарея конденсаторов со ступенчатым регулированием 94 мкФ.
4. Амперметр с пределом измерений 2А.
5. Вольтметры - 3 шт. с пределами измерений 250 В, 100 В.
Содержание работы
Исследовать дорезонансный, резонансный и послерезонансный режимы последовательной цепи изменением индуктивности при постоянной емкости и изменением емкости при постоянной индуктивности. Измерить параметры катушки при помощи амперметра, вольтметра и ваттметра.
Порядок выполнения работы
1. Собрать схему для исследования последовательной цепи (рис. 4-8).

Рис. 4-8. Схема исследования последовательной цепи
2. Ключ В1 разомкнут. Включаем выключатели батареи конденсаторов, набираем суммарную емкость 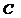 =30 мкФ. Включаем источник питания 36 В тумблером T1, цепь подмагничивания катушки тумблерами Т2, Т3. Изменяя индуктивность катушки, устанавливаем резонансный режим, который определяется по максимальному показанию амперметра Авх. Показания приборов занести в таблицу 1.
=30 мкФ. Включаем источник питания 36 В тумблером T1, цепь подмагничивания катушки тумблерами Т2, Т3. Изменяя индуктивность катушки, устанавливаем резонансный режим, который определяется по максимальному показанию амперметра Авх. Показания приборов занести в таблицу 1.
3. Изменяя, индуктивность катушки, установить дорезонансный режим (ток в цепи увеличивается), затем - послерезонансный режим (ток в цепи уменьшается). Показания приборов для одной точки дорезонансного режима и одной точки послерезонансного режима занести в табл. 4-1.
Таблица 4-1
| Режимы цепи | Данные измерений | |||||
 , В , В
|  , А , А
| 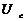 , В , В
| 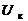 , В , В
| 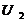 , В , В
| 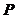 , Вт , Вт
| |
| Резонанс Дорезонансный Послерезонансный | ||||||
4. По данным табл. 4-1 построить векторные диаграммы цепи для трех режимов: резонансного, дорезонансного и послерезонансного. Диаграмму удобно строить методом засечек с помощью циркуля, в соответствии с балансом напряжений.
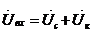
5. Установить ток I вх=0,5 А. регулированием индуктивности. Выключить батарею конденсаторов с помощью тумблеров, замкнуть ключ В1. Показания приборов занести в табл. 4-2
Таблица4- 2
| Данные измерений | Данные вычислений | |||||
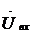 , В , В
|  , А , А
| 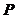 , Вт , Вт
| 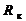 , Ом , Ом
| 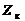 , Ом , Ом
| 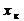 , Ом , Ом
| 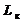 , Гн , Гн
|
6. По данным табл. 2 определить R к, Z к, x к, L к по формулам:

 ;
; 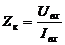 ; x к=√ Z к2- R к2 = ω L к; L к = x к/ ω.
; x к=√ Z к2- R к2 = ω L к; L к = x к/ ω.
7. Разомкнуть ключ В1. Включить суммарную емкость 30 мкФ. Изменяя индуктивность, установить резонансный режим. Оставив индуктивность неизменной, записать показания приборов при ступенчатом изменении емкости в пределах имеющегося магазина емкостей. Показания приборов занести в табл. 4-3.
Таблица4- 3
| № п/п | Данные измерений | Данные вычислений | ||||||||
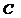 , мкФ , мкФ
 , В , В
|  , А , А
| 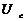 , В , В
| 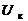 , В , В
| 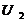 , В , В
| 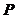 , Вт , Вт
| cos φвх | 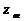 , Ом , Ом
| 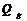
| ||
| 1. 2. 3. | ||||||||||
8. По данным табл. 4-3 построить графики зависимостей:
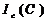 ,
,  ,
, 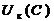 ,
, 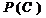 , cos φвх(С),
, cos φвх(С), 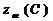 ,
, 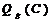 .
.
cos φвх(С) - определяется из соотношения (4.8)
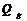 - определяется из соотношения (4.5)
- определяется из соотношения (4.5)
Содержание отчета
1. Название работы.
2. Цель работы.
3. Схему исследования.
4. Таблицу приборов и оборудования.
5. Таблицы с результатами измерений и вычислений.
6. Расчетные формулы.
7. Графики зависимостей.
8. Векторные диаграммы.
9. Выводы об особенностях резонансного и нерезонансного режимов.
Контрольные вопросы
1. Что такое резонанс напряжений?
2. Каким способом регулируется собственная частота цепи?
3. Чем определяется величина усиления напряжений?
4. Почему выходной ток при резонансе напряжений максимален?
5. Почему коэффициент мощности при резонансе равен единице, а до и после резонанса снижается?
6. Как строятся векторные диаграммы для нерезонансных режимов?
7. Почему резонансные режимы весьма экономичны?
8. Где используется резонансы напряжений?
Литература
1. Электротехника [Текст]: / Под ред. В. С. Пантюшина.- М.: Высшая школа, 1976. - гл.5, С.108 - 111.
2. Касаткин, А.С. Электротехника [Текст]: / А.С. Касаткин, М.В. Немцов; - М.: Высшая школа, 2002. - гл.12, с. 339-356.
3. Бессонов, Л.А. Теоретические основы электротехники. [Текст]: - М.: Гардарики, 2001. - §1.28.
ЛАБОРАТОРНАЯ РАБОТА №5.






