Содержание учебного материала: Классификация, строение, номенклатура, получение комплексных соединений. Виды химической связи в комплексных соединениях.
Основные понятия и термины по теме: комплексные соединения, внешняя сфера, внутренняя сфера, комплексообразователь, лиганды, коодинационное число, дентантность,константа устойчивости комплексных соединений
Методические рекомендации: При изучении темы обратить внимание на строение комплексных соединений, их структуру. Выяснить в чем заключается разница между катионными, анионными, смешанными и нейтральными комплекснымисоединениями.
Краткое изложение теоретических вопросов:
Комплексными соединениями называются определённые химические соединения, образованные сочетанием отдельных компонентов и представляющие собой сложные ионы или молекулы, способные существовать как в кристаллическом, так и в растворённом состоянии. В соответствии с координационной теорией комплексные соединения состоят из внутренней и внешней сферы. Во внутреннюю сферу входит центральный ион-комплексообразователь, окруженный связанными с ним лигандами. Внутреннюю сферу обозначают квадратными скобками. Ионами-комплексообразователями являются ионы металлов. Наибольшую склонность к комплексообразованию имеют ионы d-элементов. Вокруг центрального иона-комплексообразователя находятся противоположно заряженные ионы или нейтральные молекулы, которые называются лигандами (от лат. liqo- связываю) или аддендами. Важнейшие лиганды:
Анионы: I- - иодо, Cl- - хлоро, Br- - бромо, OH- - гидроксо, CN- - циано, NO2- – нитро, амидо - NH2-, SO42- - сульфато, тиосульфато - S2O32-, тиоцианато – SCN- карбонато - CO32-, оксалато - C2O42-
Нейтральные молекулы: NH30 – аммин, H2O0 – аква, СО0 – карбонил, NO0 – нитрозо
Число лигандов (аддендов), которые координируются вокруг центрального иона-комплексообразователя, называется координационным числом. Координационное число зависит от центрального иона, и, как правило, в 2 раза больше него.
Составляя уравнения реакций, в результате которых образуются комплексные соединения, необходимо учитывать правило определения заряда комплексного иона: заряд комплексного иона равен алгебраической сумме зарядов ионов, из которых он образовался.
Пример 1. Определить заряд комплексного иона [Fe(CN)6]x, в котором железо трёхвалентно.
Решение
Заряд железа +3, а заряд шести отрицательно одновалентных анионов одноосновной синильной кислоты равен –6. Сложим заряды: +3 + (–6) = –3.
Это и будет валентность комплексного иона.
Раствор комплексного соединения можно рассматривать как раствор слабого электролита и применять к нему законы действия масс и ионного равновесия.
Например, уравнение, выражающее процесс диссоциации комплексного иона [Fe(CN)6]3-, можно написать как уравнение обратимой реакции:
[Fe(CN)6]3- 
Fe3+ + 6CN-
и применить к нему закон ионного равновесия:
Константу диссоциации комплекса обычно называют константой нестойкости. Чем меньше константа нестойкости комплекса, тем меньше распадается комплекс на исходные ионы, т.е. он устойчивее.
Чтобы определить концентрацию исходного иона в растворе комплексного соединения, нужно составить уравнение закона ионного равновесия для данного комплекса, обозначить неизвест-ные величины через х, подставить величину константы нестойкости (из таблиц), составить вычислительную формулу и найти искомую величину.
Пример 2. Определить концентрацию ионов Hg2+ и Cl- в 0,1 М
раствореK2[HgCl4].
Решение
Так как концентрация раствора невысокая, а данная соль диссоциировала хорошо, считаем, что общая концентрация иона [HgCl4]2- также равна 0,1 моль/л.
Пишем уравнение диссоциации комплексного иона:
[HgCl4]2- 
Hg2+ + 4Cl-
Составляем формулу закона ионного равновесия:
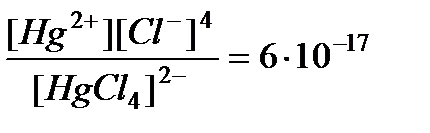(1)
(значение К взято из таблицы). Обозначим [Hg2+] через х. Тогда
[Cl-] = 4 х. [[HgCl4]2-] принимаем равной общей концентрации (0,1 моль/л), так как константа нестойкости этого комплекса очень мала. Подставляем все величины в формулу (1):
откуда 256 · х5 = 6·10-18;
Концентрация Сl–-иона будет в 4 раза больше:
[Cl-] = 4·1,2·10-4=4,8·10-4 моль/л.
Вопросы для самоконтроля:
1.Классификация, строение, номенклатура, получение комплексных соединений.
2.Виды химической связи в комплексных соединениях.
Задания для самостоятельной работы:
1. Подготовьте опорный конспект на тему:«Реакции комплексообразования. Виды химической связи в комплексных соединениях»
2.Дать названия следующим соединениям: K3[Fe(CN)6NH3], (NH4)2[Pt(OH)2Cl4], [Co(NO2)2Cl(NH3)3].
3. Написать формулы комплексных соединений: хлорид диамминсеребра (I), трифторотриаквахром, хлорид дихлоротетраамминплатины (IV), гексацианоферррат (II) калия (желтая кровяная соль), тетрагидроксохромит калия, (NH4)2{Pt(OH)2Cl4] - тетрахлорогидроксоплатинат (IV) аммония.
4. Закончите реакцию комплексообразования, назовите полученное комплексное соединение:
Zn(OH)2 + NaOH →
к.ч. = 4
5. Определить заряд комплексного иона [Fe(CN)6]x, в котором железо двухвалентно.
6. Определить концентрацию ионовZn2+ иOH- в 0,1 М
раствореNa2[Zn(OH)4]
Подготовьте доклад, реферат или презентацию на тему:
· «Биологическая роль комплексных соединений»;
· «Применение комплексных солей в медицине»;
· «Типы комплексных соединений»;
· «Теория Вагнера, ее сущность»;
· «Уникальный мир кристаллов: их строение и свойства»;
·
Список рекомендуемой литературы:
1. Пустовалова Л.М., Никанорова И.Е.Неорганическая химия. Ростов-н/Д. Феникс, 2005
2. Бабков, А.В. Общая и неорганическая химия [Текст]: учебник / А.В. Бабков, Т.И. Барабанова, В.А. Попков. – М.: ГЭОТАР-Медиа, 2014. – 384 с.
3. Егоров А.С. Химия. Пособие-репетитор для поступающих в вузы. – Ростов н/Д, Феникс, 2007
Тема 1.7.Растворы.
Содержание учебного материала: Понятие о дисперсных системах. Видыдисперсных систем: грубодисперсные системы (суспензии и эмульсии), коллоидные и истинные растворы. Понятие о растворимом веществе и растворителе. Гидратная теория растворов Д. И. Менделеева. Виды растворов. Способы выражения концентрации растворов.
Основные понятия и термины по теме: дисперсные системы, дисперсионная среда, дисперсное вещество, коллоидные, истинные растворы, взвеси, эмульсии, суспензии, гели, золи, массовая доля, молярная концентрация и молярная концентрация эквивалента.
Методические рекомендации: При изучении темы необходимо отметитьосновные положения гидратной теории растворов Д.И. Менделеева и основные виды растворов, различия между ними. Необходимо запомнить как рассчитываются следующие показатели: массовая доля, молярная концентрация и молярная концентрация эквивалента.
Краткое изложение теоретических вопросов:
Дисперсными называются гетерогенные системы, в которых одно вещество в виде очень мелких частиц равномерно распределено в объёме другого. То вещество, которое присутствует в меньшем количестве и распределено в объёме другого, называют дисперсной фазой.
Вещество, присутствующее в большем количестве, в объёме которого распределена дисперсная фаза, называют дисперсионной средой. И дисперсную фазу, и дисперсионную среду могут представлять вещества, находящиеся в различных агрегатных состояниях – твердом, жидком и газообразном.
По величине частиц веществ, составляющих дисперсную фазу, дисперсные системы делят грубодисперсные (взвеси) с размерами частиц более 100 нм и тонкодисперсные (коллоидные системы или коллоидные растворы) с размерами частиц от 100 до 1нм.
Если же вещество раздроблено до молекул или ионов менее 1 нм, образуется гомогенная система – раствор.
Взвеси – это дисперсные системы, в которых размер частиц фазы более 100нм. Это непрозрачные системы, отдельные частицы которых можно заметить невооруженным глазом. Дисперсная фаза и дисперсионная среда легко разделяются отстаиванием.
Такие системы разделяют на:
- эмульсии (среда и фаза – нерастворимые друг в друге жидкости)
- суспензии ( среда – жидкость, фаза – нерастворимое в ней твердое вещество)
- аэрозоли – взвеси в газе мелких частиц жидкостей или твердых веществ.
Многие лекарственные вещества являются взвесями.
Коллоидные системы – это такие системы, в которых размер частиц фазы от100 до 1нм. Эти частицы не видны не вооруженным глазом, и дисперсная фаза и дисперсионная среда в таких системах разделяются с трудом.
Их подразделяют на золи (коллоидные растворы) и гели (студни).
Классификация растворов:
1. По агрегатному состоянию:
‒ жидкие (плазма крови, лимфа, микстуры)
‒ твердые (таблетки, сплавы)
‒ газообразные (воздух, газовые смеси)
2. По типу растворителя жидкие растворы делятся на:
‒ водные (растворитель - вода)
‒ неводные (растворитель - спирт, бензол, эфир, ацетон и т.д.)
3. По количеству растворенных частиц:
‒ насыщенные - раствор содержит максимальное количество растворяемого вещества при данной температуре
‒ ненасыщенные - раствор содержит меньше растворяемого вещества, чем насыщенный при данной температуре
‒ пересыщенные – неустойчивые растворы, при встряхивании из них образуются насыщенные растворы, и выделяется избыток растворенного вещества
‒ концентрированные - содержат много растворенного вещества по сравнению с массой растворителя.
‒ разбавленные - содержат мало растворенного вещества по сравнению с массой растворителя.
Растворимость вещества в растворителе (воде) характеризует коэффициент растворимости. Он показывает, какая масса вещества может раствориться в 100г растворителя при данной температуре. По растворимости вещества делят на хорошо растворимые (менее 1г вещества на 100г воды), малорастворимые (от 0,001до 1г вещества на 100г воды) и практически нерастворимые (менее0, 001г на 100г воды). Растворимость веществ зависит от природы растворителя, от природы растворяемого вещества, от температуры и других факторов. Для качественной характеристики растворов используют понятия «разбавленный раствор» (содержит мало растворенного вещества) и «концентрированный раствор» (содержит много растворенного вещества).
Количественный состав растворов можно выразить путем определения массовой доли вещества в растворе и молярной концентрации раствора.
Способы выражения концентрации раствора
Концентрация раствора есть число, показывающее, сколько растворённого вещества содержится в определённой массовой или объёмной единице раствора.
Концентрацию насыщенных растворов принято выражать в граммах на 100 г растворителя. Эта величина постоянная при данной температуре и называется растворимостью.
Существует несколько способов выражения концентраций растворов.
1.1. Массовая процентная концентрация
Массовая процентная концентрация есть число, которое показывает, сколько грамм чистого растворённого вещества содержится в 100 г раствора или, другими словами, это число, которое показывает, какую массовую долю (%) составляет раство-рённое вещество в растворе.
Массовую процентную концентрацию (или массовую долю растворённого вещества в растворе) можно рассчитать по формуле:
,
где: m (р.в.) – масса растворённого вещества;
m (раствора) – массовая доля растворённого вещества.
Пример 1. Сколько г хлористого натрия и воды следует взять для приготовления 80 г раствора с массовой долей хлорида натрия в растворе 5%?
Решение
Из формулы 
найдём:
Ответ: 4 г NaCl, воды 80 – 4 = 76 г
Эту же задачу можно решить вторым способом, путём составления пропорций:
Решение
В 100 г раствора должно содержаться 5 г хлорида натрия т.к. массовая доля его в растворе 5%. Составим и решим пропорцию:
в 100 г раствора содержится 5 г хлорида натрия
в 80 г раствора содержится Х г хлорида натрия
Разность 80 – 4 = 76 равна массе растворителя, необходимой для приготовления 80 г 5%-ного раствора из 4 г соли.
1.2 Молярная концентрация
Молярная концентрация или молярность – это число, которое показывает, сколько молей растворённого вещества содержится в 1 л раствора.
Обозначается молярность буквой М. Масса вещества, соответ-ствующая 1 моль его называется молярной массой. Она выражается в г/моль и численно равна относительной молекулярной массе М r.
Пример 2. Сколько г CuSO4·5H2O потребуется для приготовления
2 л 4 М раствора?
Решение
Найдём молекулярную массу CuSO4·5H2O: M r (CuSO4·5H2O) = 250 1 моль CuSO4·5H2O, т.е. молярная масса этой соли равна:
Составим и решим две пропорции:
1. Для 1 л 1 М раствора требуется 250 г соли
2 л 1 М раствора требуется Х г соли
2. Для 2 л 1 М раствора требуется 500 г соли
2 л 4 М раствора требуется Х г соли
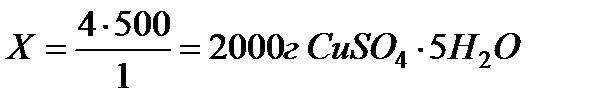
Ответ: для приготовления 2 л 4 М раствора потребуется 2000 г
CuSO4·5H2O.
Пример 3. Определить молярность раствора, содержащего 80 г
NaOH в 500 мл раствора.
Решение
1. Определяем массу щёлочи в 1 л раствора:
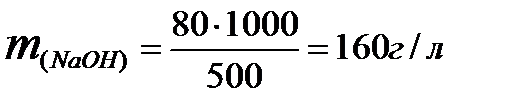
2. Находим молярность раствора делением массы NaOH в 1 л
раствора на его молярную массу:
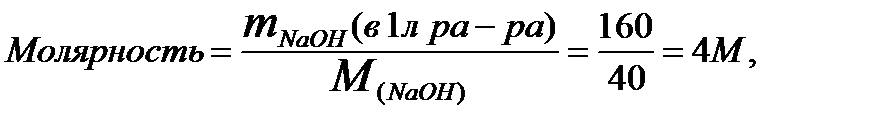
где: М (NaOH) = 40 г/моль
Ответ: молярность раствора равна 4 моль/л.
1.3 Нормальная концентрация
Нормальностью раствора называется число, показывающее, сколько моль эквивалентов растворённого вещества содержится в 1 л раствора.
Задачи на определение нормальности раствора решаются точно так же как и на вычисление молярности, но вместо молярной массы берётся её эквивалентная масса. Об эквивалентности раствора вообще можно говорить применительно к конкретной химической реакции. Вам надлежит вспомнить нахождение эквивалентов солей, кислот, оснований, окислителей и восстановителей.
Обратите внимание, что эквивалент окислителя и восстановителя зависит от числа электронов, присоединяемых одной молекулой окислителя или отданных одной молекулой восстановителя.
Пример 4. Рассчитать эквивалентные массы азотной кислоты, если
она восстанавливается до: а) NO2; б) NO; в)NH4+.
Решение
а) HNO3 → NO2; NO3- + 2H+ + 1ē → NO2 + H2O
б) HNO3 → NO; NO3- + 4H+ + 3ē → NO + 2H2O
в) HNO3 → NH4+; NO3- + 10H+ + 8ē → NH4+ + 3H2O
Навеску для приготовления растворов нормальной концентрации можно вычислить по формуле:
где: С э – нормальность раствора;
V – объём раствора в миллилитрах.
Пример 5. Сколько нужно взять сульфата алюминия для
приготовления 400 мл 0,1 н раствора?
Решение
1. Рассчитаем молярную и эквивалентную массы сульфата
алюминия:
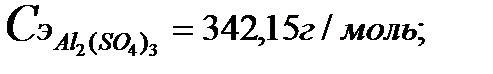
2. Рассчитаем массу Al2(SO4)3 по формуле:
Ответ: необходимо взять 2,28 г Al2(SO4)3.
1.4 Переход от одних систем выражения
концентрации к другим
Перейти от массовой процентной концентрации к молярной или нормальной (и обратно) можно только в том случае, если известна плотность раствора, т.к. массовая процентная концентрация указывает на содержание вещества в определённом весовом количестве раствора (в 100 мас.ч.), а молярная и нормальная – в определённом объёме (в 1 л). При решении задач этого типа можно воспользоваться общими формулами перевода массовой процент-ной концентрации раствора в выражения нормальной и молярной концентрации и наоборот:
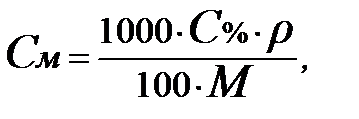
где: С н, С м, С % - нормальные, молярные и массовые процентные
концентрации;
ρ – плотность раствора;
М э – эквивалентная масса;
М – молярная масса.
Пример 6. Определить молярность раствора серной кислоты
с массовой долей (%) H2SO4 в растворе – 62%.
Решение
Определить молярность раствора – это значит узнать, сколько молей безводной серной кислоты содержится в 1 л её раствора. Плотность 62%-ного раствора равна 1,520 г/см3 (из таблицы). Следовательно, масса 1 л раствора серной кислоты равна 1520 г.
1. Массу безводной H2SO4 в 1 л раствора найдём из формулы для
вычисления массовой доли (%) растворённого вещества:
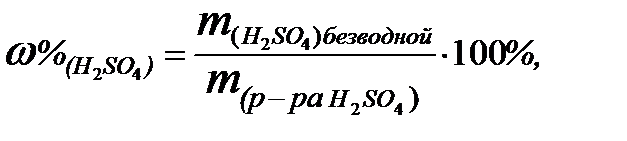
откуда: 
можно найти другим способом, составив и решив
пропорцию:
в 100 г раствора H2SO4 (ω % = 62%) – 62 г H2SO4 (безводной)
в 1520 г — // — // — // — // — – Х г — // — // — // —
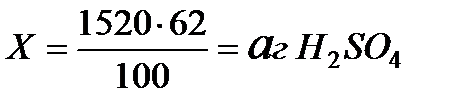
2. Молярность рассчитаем делением массы H2SO4 в 1 л раствора на
молярную массу H2SO4 (M H2SO4 = 98 г/моль).
Пример 7. Сколько мл 10%-ного раствора H2SO4 нужно взять для
приготовления 2 л 0,5 М раствора?
Решение
1. Рассчитаем молярную массу H2SO4:
М H2SO4 = 1·2 + 32 + 16·4 = 98 г/моль.
2. Рассчитаем, сколько г серной кислоты содержит 2 л 0,5 М
раствора, решив пропорцию:
в 1 л 0,5 М раствора содержится (0,5·98) г H2SO4
в 2 л — // — // — // — // — Х г 
H2SO4
3. Находим, в какой массе 10%-ного раствора содержится 98 г
H2SO4:
в 100 г 10%-ного раствора содержится 10 г H2SO4
в Х г — // — // — // — // — // — 98 г H2SO4
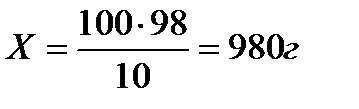раствора H2SO4
4. Вычислим объём 10%-ного раствора серной кислоты,
воспользовавшись формулой:
,
ρ10% H2SO4 = 1,07 г/см3 (из таблицы).
Поставим значение ρ и m в формулу: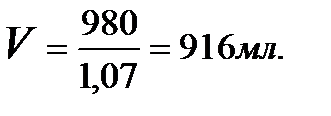 
Ответ: следует взять 916 мл 10%-ной H2SO4
Если раствор разбавить водой, то его концентрация изменится обратно пропорционально изменению объёма. Если от разбавления объём раствора увеличится в два раза, то его концентрация в два раза уменьшится. То же самое происходит при смешивании нескольких растворов, при этом уменьшаются концентрации всех смешиваемых растворов.
Пример 8. Смешаны вместе: 5 мл 1 М раствора вещества А, 3 мл 2 М раствора вещества Б и 2 мл 4 М раствора вещества В. Найти концентрации каждого вещества в растворе после смешивания.
Решение
Общий объём раствора после смешивания:
5 + 2 + 3=10 мл.
Следовательно, концентрация нового раствора в отношении каждого из веществ, растворённых в первоначальных растворах, соответственно уменьшилась. Если объём раствора вещества А до смешивания был 5 мл, а после смешивания то же самое количество этого вещества стало находиться уже в 10 мл, концентрация А после смешивания уменьшилась в 2 раза.
Аналогично изменились концентрации двух других растворов:
Чтобы вычислить соотношения, в каких следует взять два раствора известных концентраций для получения раствора заданной концентрации, пользуются правилом креста. Пользуясь этим способом, две прямые линии располагают «косым» крестом. В центре креста пишут величины концентраций исходных растворов: большую – сверху, меньшую – снизу. В конце линий креста справа пишут искомые количества растворов, которые получают вычитанием по диагонали из большей величины меньшей.
Пример 9. В каком отношении следует смешать 90%-ный раствор серной кислоты с 10%-ным, чтобы получить 40%-ный раствор?
Решение
По правилу креста находим:
90% 30 40 – 10 = 30 массовых частей
40%
10% 50 90 – 40 = 50 массовых частей
Таким образом, следует взять 30 мас.ч. 90%-ного раствора и прибавить к ним 50 мас.ч. 10%-ного.
Если в задаче требуется узнать, какие количества растворов данной концентрации следует взять, чтобы получить заданное количество раствора новой концентрации, то сначала определяют их соотношение, как в примере 6, а потом делят заданное количество пропорционально этому отношению.
Пример 10. Какие количества 90 и 10%-ного растворов серной кислоты нужно взять, чтобы приготовить 1600 г 40%-ного раствора?
Решение
По правилу креста находим соотношение растворов с массовыми долями (%) серной кислоты 90% и 10%:
90% 30 массовых частей
40%
10% 50 массовых частей
Затем делим 1600 г на две части, пропорциональные этому соотношению.
90%-ного раствора H2SO4 следует взять:
10%-ного раствора H2SO4 следует взять:
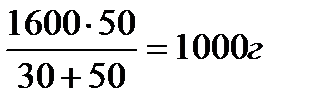
Задачи на разбавление растворов чистым растворителем можно также решать на основании закона смешений, применяя правило креста. В таких случаях чистый растворитель считают за второй раствор с концентрацией 0.
Пример 11. Сколько воды нужно прибавить к 100 г раствора с массовой долей (%) NH3 – 25%, чтобы получить раствор с массовой долей (%) NH3 – 5%?
Решение
Пользуясь правилом креста, определяем соотношение количест-ва исходного раствора и воды.
25% 5 массовых частей
5%
0 20 массовых частей
На 5 мас.ч. раствора с массовой долей (%) NH3 – 25% следует взять 20 мас.ч. Н2О.
Составим пропорцию:
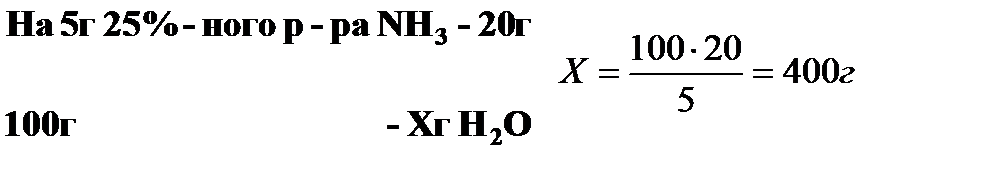
Ответ: количество воды, необходимое для приготовления
раствора, составляет 400 г.
При решении задач, в которых концентрация растворов выражена в молях или нормалях, исходят также из закона смешения, но количество растворов выражают в литрах или его долях.
Пример 12. Сколько миллилитров 0,5 М и 0,1 М растворов следует
взять для приготовления 1000 мл 0,2 М раствора?
Решение
0,5 0,1 объёмных единиц = 1 об.ед.
0,2 
0,1 0,3 объёмных единиц = 3 об.ед.
0,5 М раствора следует взять:
; 1000 – 250 = 750 мл 0,1 М раствора.
Вопросы для самоконтроля:
1. Понятие о дисперсных системах. Виды дисперсных систем: грубодисперсные
системы (суспензии и эмульсии), коллоидные и истинные растворы.
2. Понятие о растворимом веществе и растворителе.
3. Гидратная теория растворов Д. И. Менделеева.
4. Виды растворов.
5. Способы выражения концентрации растворов. Массовая доля, молярная
концентрация и молярная концентрация эквивалента.
Задания для самостоятельной работы:
Составить таблицу: «Сравнительная характеристика дисперсных систем».
Решите следующие задачи:
1. Определить массовую долю NaCl в растворе, который содержит 53,5г NaCl в500см3 раствора. Плотность раствора 1,07 г/см3
2. Какова масса Na2CO3, содержащаяся в 0,2 дм3 0,3 молярного раствора?
3. Определить мольную часть глюкозы в водном растворе глюкозы с массовой долей 36%.
4. При некоторых заболеваниях в организм вводят раствор хлористого натрия с массовой долей 0,9%, называемый физиологическим раствором. Вычислите, сколько воды и соли нужно взять для приготовления 250 мл физиологического раствора, плотность которого 1,005 г/см3.
5. Для компенсации недостатка соляной кислоты в желудочном соке применяют ее растворы как лекарственные формы. Сколько мл НС1 с массовой долей 26% (пл. 1,12 г/см3) необходимо для приготовления 200 мл 0,1 н раствора НС1?
6. Для приготовления 0,025М раствора хлорида кальция используют СаСl2 в ампулах с массовой долей 0,45% (пл. 1,04 г/см3). Сколько мл этого раствора необходимо для приготовления 500 мл 0,02 5М раствора?
Подготовьте доклад, реферат или презентацию на тему:
· «Гидратная теория растворов Д.И. Менделеева и ее современное значение»;
· «Коллоидные растворы. Их применение в быту, фармации»;
· «Биологическая роль коллоидных растворов»;
· «Вода - уникальный растворитель»;
· Истинные растворы, их биологическая роль дляжизнедеятельности живых организмов»;
Список рекомендуемой литературы:
1. Пустовалова Л.М., Никанорова И.Е.Неорганическая химия. Ростов-н/Д. Феникс, 2005
2. Бабков, А.В. Общая и неорганическая химия [Текст]: учебник / А.В. Бабков, Т.И. Барабанова, В.А. Попков. – М.: ГЭОТАР-Медиа, 2014. – 384 с.
3. Егоров А.С. Химия. Пособие-репетитор для поступающих в вузы. – Ростов н/Д, Феникс, 2007
