Внутренняя норма доходности ( IRR )

Внутренняя норма доходности (ВНД) представляет собой ту норму дисконта (Евн), при которой величина приведенных эффектов равна приведенным капиталовложениям.

Т (Rt-3* t)   Т Kt

Σ -----------  = Σ-------------                                        (10)

t=0                  t    t=0                  t

 (1 + Евн)                           (1 + Евн)

При использовании внутренней нормы доходности (ВНД) следует соблюдать известную осторожность. Во-первых, она не всегда суще­ствует. Во-вторых, уравнение (10) может иметь больше одного ре­шения. Первый случай весьма редок. Во втором корректный расчет ВНД несколько затруднителен, хотя и возможен. В качестве первого приближения к ситуации, когда простой (недисконтированный) инте­гральный эффект положителен, предлагается принимать в качестве внутренней нормы дисконта (Евн) значение положительного корня уравнения (9), который представляет собой ту норму дисконта (Евн), при котором величина приведенных эффектов равна приведен­ным капиталовложениям.

Если расчет ЧДД инвестиционного проекта дает ответ на вопрос, является он эффективным или нет при некоторой заданной норме дисконта (Е), то ВНД проекта определяется в процессе расчета и за­тем сравнивается с требуемой инвестором нормой дохода на вклады­ваемый капитал.

В случае, когда ВНД равна или больше требуемой инвестором нормы дохода на капитал, инвестиции в данный инвестиционный проект оправданы, и может рассматриваться вопрос о его принятии противном случае инвестиции в данный проект нецелесообразны.

Если сравнение альтернативных (взаимоисключающих) инвестиционных проектов (вариантов проекта) по ЧДД и ВНД приводят к противоположным результатам, предпочтение следует отдавать ЧДД.

Внутреннюю норму доходности можно определить по формуле, построенной по методу интерполяции:

 

 С

(11)

Евн = А+ -------- * (В – А), где

 С -Д

А - ставка дисконта при отрицательном чистом дисконтированном доходе;

В - ставка дисконта при положительном чистом дисконтированном доходе;

С - чистый дисконтированный доход при ставке дисконта А;

Д - чистый дисконтированный доход при ставке дисконта В.

Метод интерполяции дает только приближенное значение внутренней нормы доходности. Чем больше расстояние между любыми двумя точками, имеющими положительный и отрицательный чистый дисконтированный доход, тем менее точным будет подсчет внутренней нормы доходности.

Срок окупаемости (PB)

Срок окупаемости (Ток) - минимальный временной интервал (от начала осуществления проекта), за пределами которого интегральный эффект становится и в дальнейшем остается неотрицательным.

Иными словами, это период (измеряемый в месяцах, кварталах и годах), начиная с которого первоначальные вложения и другие затраты, связанные с инвестиционным проектом, покрываются суммарными результатами его осуществления.

Результаты и затраты, связанные с осуществлением проекта, можно вычислять с дисконтированием или без него. Соответственно, получится два различных срока окупаемости.

Срок окупаемости рекомендуется определять с использованием дисконтирования (дисконтированный период окупаемости).

Срок окупаемости можно определить и графическим путем (см. рис.8.5), если в зависимости от года реализации проекта построить две кривые, одна из которых будет обозначать единовременные и текущие дисконтированные затраты нарастающим итогом, а вторая - дисконтированные текущие результаты (поступления) нарастающим итогом.

Полученные результаты расчета показателей экономической эффективности сводятся в общую таблицу (см. таблицу 8.7).

 

 

 

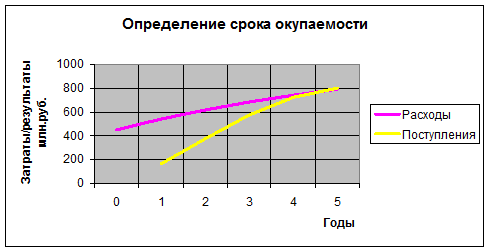Рисунок 8.5 - Пример дисконтированного периода окупаемости

 

Таблица 8.7 - Эффективность проекта

Показатель	Значение
Ставка дисконтирования, %
Период окупаемости - PB, мес.
Дисконтированный период окупаемости - DPB, мес.
Чистый приведенный доход – NPV, руб.
Индекс прибыльности - PI
Внутренняя норма рентабельности - IRR, %

 

 

[1] См. ФГОС ВПО по направлению подготовки 080200 «Менеджмент», утвержденный приказом Минобрнауки России от 20.05.2010 №544.

[2] Бекетова О.Н, Найденков В.И. Бизнес-план: теория и практика. – М.: Издательство «Альфа-Пресс», 2006. – 272 с.

[3] Белоусов В.Л., Горбунов В.Л. Бизнес-план инновационного проекта. Методология создания. Учебное пособие. М.: ФГУ НИИ РИНКЦЭ, 2005 – 176 с.

[4] Имеет смысл рассматривать для организаций существующих на рынке длительное время (свыше 5 лет) или претерпевшие коренные перестройки в системе своей деятельности

[5] Рыночная реализация - это фактический (или предполагаемый) объем продаж для определенной категории покупателей в определенном географическом районе за определенный период времени.

[6] В случае, когда между предприятием и конечным потребителем стоит группа посредников: оптовые торговцы (дистрибьюторы), розничные торговцы и т.п.

[7] Белоусов В.Л., Горбунов В.Л. Бизнес-план инновационного проекта. Методология создания. Учебное пособие. М.: ФГУ «НИИ РИНКЦЭ», 2005. 176 с. (с.112).

[8] Виленский П.Л., Лившиц В.Н., Смоляк С.А. Оценка эффективности инвестиционных проектов: Теория и практика: Учеб.пособие. – 2-е изд., перераб. и доп. – М.: Дело, 2002. – 888 с.(с.147)

[9] [9] Виленский П.Л., Лившиц В.Н., Смоляк С.А. Оценка эффективности инвестиционных проектов: Теория и практика: Учеб.пособие. – 2-е изд., перераб. и доп. – М.: Дело, 2002. – 888 с.(с.169)

 

[10] Кочетков А.И. Экономика предприятия: Учебное пособие. Издание второе, переработанное и дополненное. - М.: ИПАК, 2003.-272 с.