Ответ:Относительная статистическая величина — это результат соотношения двух абсолютных статистических величин.
Если соотносятся абсолютные величины с одинаковой размерностью, то получаемая относительная величина будет безразмерной (размерность сократится) и носит название коэффициент.
Часто применяется искусственная размерность коэффициентов. Она получается путем их умножения:
на 100 — получают проценты (%);
на 1000 — получают промилле (‰);
на 10000 — получают продецимилле (‰O>).
Искусственная размерность коэффициентов применяется, как правило, в разговорной речи и при формулировании результатов, а в самих расчетах она не используется. Чаще всего применяются проценты, в которых принятно выражать полученные значения относительных величин.
Чаще вместо названия относительная статистическая величина используется более краткий термин-синоним — индекс (от лат. index — показатель, коэффициент).
В зависимости от видов соотносимых абсолютных величин при расчете относительных величин, получаются разные виды индексов: динамики, планового задания, выполнения плана, структуры, координации, сравнения, интенсивности.
Индекс динамики (коэффициент роста, темп роста) показывает во сколько раз изменилось изучаемое явление или процесс во времени. Рассчитывается как отношение значения абсолютной величины в отчетный (анализируемый) период или момент времени к базисному (предыдущему):
 .
.
Здесь и далее подиндексы означают: 1 — отчетный (анализируемый) период, 0 — базисный (прошлый) период.
Критериальным значением индекса динамики служит "1", то есть: если iД>1 - имеет место рост явления во времени; если iД=1 — стабильность; если iД<1 - наблюдается спад явления.
Если из индекса динамики вычесть его критериальное значение "1" и выразить полученное значение в процентах, то получится темп изменения с критериальным значением "1":
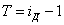
Если T>0, то имеет место рост явления; Т=0 – стабильность, Т<0 — спад.
В некоторых учебниках индекс динамики называется коэффициентом роста или темпом роста, а темп изменения — темпом прироста, независимо от получаемого результата, который может показать не только рост, но и стабильность или спад. Поэтому более логичным и чаще используемыми названиями являются именно индекс динамики и темп изменения.
Индекс планового задания – это отношение планового значения абсолютной величины к базисному:

Индекс выполнения плана – это отношение фактически полученного значения абсолютной величины в отчетном периоде к запланированному:

Индекс структуры ( доля, удельный вес) - это отношение какой-либо части статистической совокупности к сумме всех ее частей:

Индекс структуры показывает, какую долю составляет отдельная часть совокупности от всей совокупности.
Индекс координации - это отношение одно части статистической совокупности к другой ее части, принятой за базу сравнения:

Индекс координации показывает, во сколько раз больше или сколько процентов составляет одна часть статистической совокупности по сравнению с другой ее частью, принятой за базу сравнения.
Индекс сравнения - это отношение значений одной и той же абсолютной величины в одном и том же периоде или моменте времени, но для разных объектов или территорий:

где А, Б — признаки сравниваемых объектов или территорий.
Индекс интенсивности - это отношение значений двух взаимосвязанных абсолютных величин с разной размерностью, относящихся к одному объекту или явлению.

БИЛЕТ №11
1. Понятие, сущность средней величины и ее применение в анализе статистической информации
Ответ: Понятие, сущность средней величиныи ее применение в анализе статистической информации.
Средние величины представлют собой наиболее распространенную форму сводных величин. Они дают общую количественную характеристику элементов массового процесса, связаную или с общим качеством, присущим всем элементам массового процесса, или с общими условиями, которые определяют данный процесс.
Средняя величина – это обобщающая количественная характеристика совокупности однотипных явлений по одному варьирующему признаку. Она отражает объективный уровень, достигнутый в процессе развития явления к определенному моменту или периоду. Средняя величина представляет значение определенного признака в совокупности одним числом и элиминирует индивидуальные различия значений отдельных величин совокупности. Важнейшая особенность средней величины – она относится к единице изучаемой совокупности и через характеристику единицы характеризует всю совокупность в целом.
К основным свойствам средней величины можно отнести следующее: она обладает устойчивостью, что позволяет выявлять закономерности развития явлений; средняя облегчает сравнение двух совокупностей, обладающих различной численностью, она помогает охарактеризовать развитие уровня явления во времени, и выявить и охарактеризовать связь между явлениями.
Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.
Если исследуется совокупность с качественно однородными признаками, то средняя величина выступает здесь как типическая средняя. Например, для групп работников определенной отрасли с фиксированным уровнем дохода определяется типическая средняя расходов на предметы первой необходимости, т.е. типическая средняя обобщает качественно однородные значения признака в данной совокупности, каковым является доля расходов у работников данной группы на товары первой необходимости.
Средние позволяют исключить влияние индивидуальных значений признака, т.е. они являются абстрактными величинами. Поэтому средние должны употребляться на основе сгруппированных данных.
К расчету средней предъявляются два основных требования:
- среднюю нужно рассчитывать так, чтобы она погашала то, что мешает выявлению характерных черт и закономерностей в развитии явления, а не затушевывала развитие;
- средняя может быть вычислена только для однородной совокупности.
Расчет средних величин производится по правилам, которые разрабатываются математической статистикой. Задача теории статистики – дать смысловую, преимущественно экономическую интерпретацию результатам расчетов, произведенных по формулам.
В статистической практике используется множество видов средних: средняя гармоническая, средняя арифметическая, средняя геометрическая, средняя квадратическая, структурные средние- мода и медиана.
Мода - это значение признака, которое встречается в ряду распределения чаще, чем другие его значения. Медиана - это центральное значение признака, им обладает центральный член ранжированного ряда.
БИЛЕТ №12






