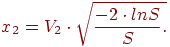Лекция: Генерирование на ЭВМ последовательностей равномерно распределенных случайных чисел. Моделирование нормально распределенной случайной величины

 

В стандартном математическом и программном обеспечении различных типов ЭВМ имеются специальные процедуры и подпрограммы для генерации равномерно распределенных последовательностей псевдослучайных чисел.

В настоящее время все языки высокого уровня имеют программные генераторы равномерно распределенных последовательностей псевдослучайных чисел. Их называют датчиками случайных чисел. Датчики случайных чисел, как правило имеют имена: RAN, RAND, RANDU, RND, RANDOM, RANDOMIZE и т.д. Эти имена получены от английского слова random, означающего случайный или выбранный наугад. Поэтому датчики случайных чисел иногда называют рандомизаторами.

Датчики случайных чисел обычно генерируют последовательность действительных чисел Un, равномерно распределенных между нулем и единицей, т.е. последовательность случайных дробей в интервале [0,1]. Но вначале датчики генерируют последовательность целых случайных чисел x_i в интервале от нуля до m, где m – размер машинного слова (на единицу больше максимального целого числа, размещающегося в машинном слове).

Как уже говорилось, для 32-х разрядного машинного слова:

m = 2³¹ = 2147483648;

1/m = 0.4656613 E-9.

Приведем датчик равномерно распределенных случайных чисел RANDU.

Этот датчик специально предназначен для системы IBM и образует 2²⁹ значений перед началом повторений, т.е. длина цикла равна 2²⁹ (при 32-х разрядном машинном слове). Алгоритм датчика реализует метод остатка степеней (рис. 8.1).

Назначение датчика RANDU:

Вычисление равномерно распределенных случайных действительных чисел YF в интервале [0,1] и случайных целых чисел IY в интервале [0,2³¹]. В качестве входа служит целое случайное число IX, на выходе образуется новое целое число IY и вещественное YF.

Обращение к датчику:

RANDU (IX,IY,YF).

Описание параметров:

IX – при первом обращении – нечетное целое число с числом цифр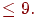

После первого обращения IX=IY, где IY – целое число, вычисленное при предыдущем обращении.

IY – полученное в результате целое случайное число, требуемое при последующих обращениях. IY находится в интервале [0, 2³¹].

YF– полученное в результате равномерно распределенное действительное число в интервале [0,1], представленное в форме с плавающей запятой.

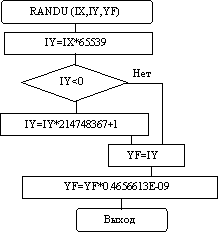
Рис. 8.1. Алгоритм датчика RANDU

Используя датчик RANDU, построим алгоритм вычисления последовательности равномерно распределенных случайных чисел и ее печать (рис. 8.2).

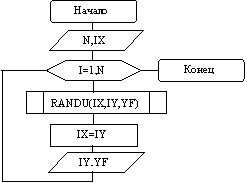
Рис. 8.2.

Алгоритм вычисления последовательности равномерно распределенных случайных чисел.

Исходные данные:

N - длина последовательности (количество испытаний).

IX - начальное значение, нечетное целое число с числом цифр <9.

Например: IX = 1234567.

Различные начальные значения параметра IX позволяют формировать различные последовательности равномерно распределенных псевдослучайных чисел.

Для генерирования равномерно распределенных случайных чисел на отрезке [0,1] используется отделение дробной части от сложного арифметического выражения, содержащего предшествующее число.

V_i+1 =FRAC(k V_i)

FRAC – оператор выделения дробной части,

V_i - предшествующее случайное число,

V_i+1 - последующее случайное число,

k-8t = 3,

t - нечетное целое число.

Задание различных начальных значений V₀ позволяет формировать различные последовательности случайных чисел.

Количество случайных чисел в одном периоде от нескольких тысяч до сотен тысяч.

Для перевода равномерно распределенных случайных чисел из отрезка [0,1] в отрезок [а,b] можно использовать:

x_i+1= a + (b-a)V_i+1.

Задачу моделирования случайных величин с нормальным законом распределения решают в несколько этапов:

1. Вначале имитируют равномерное распределение и получают последовательность псевдослучайных чисел, равномерно распределенных на интервале [0,1].
2. Затем, используя равномерно распределенную псевдослучайную величину, получают последовательность псевдослучайных чисел с нормальным законом распределения (чаще всего в нормированном виде, т.е. М(X) = 0. ).

Пусть Y – равномерно распределенная случайная величина на интервале, [0,1]. Необходимо получить случайную величину X c нормальным законом распределения.

Различают три основных способа формирования последовательности нормально распределенных случайных величин:

1. Прямое преобразование псевдослучайного числа y являющегося реализацией случайной величины Y, равномерно распределенной на интервале [0,1], с помощью некоторой функции W в число x, которое может рассматриваться как реализация случайной величины X, имеющей нормальный закон распределения.
2. Отсеивание псевдослучайных чисел из первоначальной последовательности Y равномерно распределенной на интервале [0,1], таким образом, чтобы оставшиеся числа были распределены по нормальному закону.
3. Моделирование условий, соответствующих центральной предельной теореме теории вероятности.

Рассмотрим некоторые методы моделирования нормально распределенной случайной величины.

Метод полярных координат относится к первому способу получения последовательности псевдослучайных чисел с нормальным законом распределения. Метод вычисляет две независимые нормально распределенные случайные величины x₁ и x₂ со средним значением, равным нулю, и среднеквадратичным отклонением, равным единице, по двум заданным независимым равномерно распределенным случайным числам y₁ и y₂.

Алгоритм метода:

1. Выработать два независимых случайных числа y₁ и y₂, равномерно распределенных в интервале [0,1].
2. Установить:

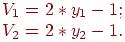
Теперь величины V₁ и V₂ равномерно распределены в интервале [-1;+1] и их удобно представить в форме с плавающей запятой.

1. Установить:

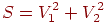
1. Проверить условие: 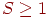Если "да ", то необходимо вернуться к шагу 1. Если "нет", то переходим к шагу 3.
2. Вычисляем x₁ и x₂:

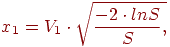
(8.1)

1. 

5. Полученные величины x₁ и x₂ – это требующиеся значения нормально распределенных случайных величин со средним значением равным нулю, и среднеквадратичным отклонением .

1. При других значениях среднего и среднеквадратичного отклонения 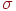делаем пересчет:

Метод полярных координат легко доказать, воспользовавшись аналитической геометрией. Рассмотрим плоскость, определенную декартовыми координатами V₁ и V₂. С помощью шагов 1 и 2 метода мы получаем на плоскости равномерно распределенные случайные точки с декартовыми координатами (V₁,V₂) и полярными координатами 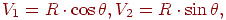где R²=S. Далее, с помощью шагов 3 и 4 метода, мы из этих случайных точек оставляем только те точки, которые находятся внутри единичного круга.

 

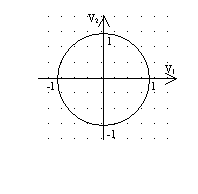
При этом попадание точек внутрь единичного круга подчиняется закону нормального распределения со средним значением равным нулю, и среднеквадратичным отклонением равным единице.

Переходя к полярным координатам точек, которые равномерно распределены внутри единичного круга имеем

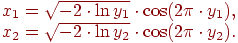
(8.2)