Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.
Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
Дано нелинейное уравнение:
| (4.1) |
Необходимо решить это уравнение, т. е. найти его корень 
.
Рис. 4.1.
Если функция имеет вид многочлена степени m,
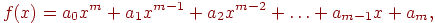
где ai - коэффициенты многочлена, 
, то уравнение f(x)=0 имеет m корней (рис. 4.2).
Рис. 4.2.
Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x, то уравнение (4.1) называется трансцендентным уравнением.
Примеры:
Такие уравнения обычно имеют бесконечное множество решений.
Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений.
Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.
Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности. Для этого используются приближенные (численные) методы решения.
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b], в котором лежит уточняемый корень уравнения (рис. 4.3).
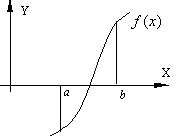
Рис. 4.3.
Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения, называется отделением этого корня.
Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b)<0, то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.
Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:
1. отделение корней, - т.е. определение интервалов изоляции [a,b], внутри которого лежит каждый корень уравнения;
2. уточнение корней, - т.е. сужение интервала [a,b] до величины равной заданной степени точности 
.
Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:
1. метод половинного деления (метод дихотомии);
2. метод простых итераций;
3. метод Ньютона (метод касательных);
4. модифицированный метод Ньютона (метод секущих);
5. метод хорд и др.
Метод половинного деления
Дано нелинейное уравнение:
|
| (4.1) |
Найти корень уравнения, принадлежащий интервалу [a,b], с заданной точностью .
Для уточнения корня методом половинного деления последовательно осуществляем следующие операции:
- Делим интервал пополам:
- В качестве нового интервала изоляции принимаем ту половину интервала, на концах которого функция имеет разные знаки (рис.4.4).
Рис. 4.4.
Для этого:
a) Вычисляем значение функции f(x) в точках a и t.
b) Проверяем: если f(a)f(t) < 0, то корень находится в левой половине интервала [a,b] (рис.4.4.а). Тогда отбрасываем правую половину интервала и делаем переприсвоение b=t.
c) Если f(a)f(t) < 0 не выполняется, то корень находится в правой половине интервала [a,b] (рис.4.4.б). Тогда отбрасываем левую половину и делаем переприсвоение a=t. В обоих случаях мы получим новый интервал [a,b] в 2 раза меньший предыдущего.
- Процесс, начиная с пункта 1, циклически повторяем до тех пор, пока длина интервала [a,b] не станет равной либо меньшей заданной точности, т.е.
Схема алгоритма уточнения корней по методу половинного деления представлена на рис. 4.5.
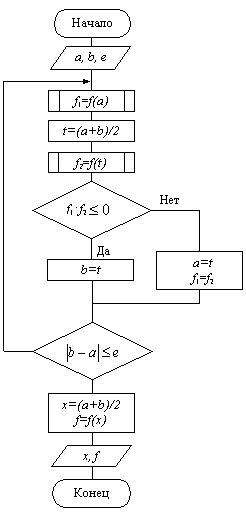
Рис. 4.5. Схема алгоритма уточнения корней по методу половинного деления
Метод простых итераций
В ряде случаев весьма удобным приемом уточнения корня уравнения является метод последовательных приближений (метод итераций).
Пусть с точностью необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.
Для применения этого метода исходное уравнение f(x)=0 должно быть приведено к виду
| (4.2) |
В качестве начального приближения 0 выбираем любую точку интервала [a,b].
Далее итерационный процесс поиска корня строится по схеме:
| (4.3) |
В результате итерационный процесс поиска реализуется рекуррентной формулой (4.3). Процесс поиска прекращается, как только выполняется условие
| (4.4) |
или число итераций превысит заданное число N.
Для того, чтобы последовательность х1, х2,…, хn приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:
| (4.5) |
Рис. 4.6. Геометрический смысл метода
Переходим к построению схемы алгоритма (рис. 4.7). Вычисление функции 
оформим в виде подпрограммы.
Рис. 4.7. Схема алгоритма уточнения корня методом итераций
Метод Ньютона (метод касательных)
Рассмотренные ранее методы решения нелинейных уравнений являются методами прямого поиска. В них для нахождения корня используется нахождение значения функции в различных точках интервала [a,b].
Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.
Дано нелинейное уравнение:
f(x)=0Найти корень на интервале [a,b] с точностью .
Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Х дает приближение корня (Рис. 4.8).
Выберем начальную точку x0=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Х дает нам первое приближение корня x1.
Рис. 4.8.
где
Поэтому
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой
| (4.6) |
Процесс поиска продолжаем до тех пор, пока не выполнится условие:
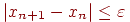
| (4.7) |
Упростим условие (4.7), исходя из (4.6). Получим:
| (4.8) |
Метод обеспечивает быструю сходимость, если выполняется условие:
| (4.9) |
т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x0) и ее кривизны f"(x0) совпадают.
Схема алгоритма уточнения корня метод Ньютона приведена на рис. 4.9
Рис. 4.9. Схема алгоритма уточнения корня методом Ньютона
Модифицированный метод Ньютона (метод секущих)
В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:
Тогда рекуррентная формула (4.6) будет иметь вид:
| (4.10) |
где 
Метод хорд
Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня.
При этом в процессе поиска семейство хорд может строиться:
а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х0=b (рис. 4.10а);
б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х0=a (рис. 4.10б);
Рис. 4.10.
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:
для случая а)
| (4.11) |
для случая б)
| (4.12) |
Процесс поиска продолжается до тех пор, пока не выполнится условие
| (4.13) |
Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f"(z) совпадают.
Схема алгоритма уточнения корня методом хорд представлена на рис. 4.11.
увеличить изображение
Рис. 4.11. Схема алгоритма уточнения корня методом хорд
