Лекция: Случайные события, случайные величины. Их законы распределения и числовые характеристики

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Обозначим: X, Y, Z – случайные величины

x_i, y_i, z_i – возможные значения случайных величин.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения или с определенными вероятностями.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины, независимо от величины промежутка, бесконечно

Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность.

Законом распределения дискретной случайной величины называют соответствие между ее возможными значениями и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) и графически (в виде многоугольника распределения).

Табличное задание закона распределения:

возможные значения случайной величины;

вероятности появления случайной величины.

Аналитическое задание закона распределения:

Биномиальное распределение, определяемое законом Бернулли

k = 0, 1, 2, …, n – количество возможных появлений событий

q = 1-p – вероятность не появления событий.

Распределение Пуассона, определяемое асимптотической формулой Пуассона:

где:

- интенсивность потока событий.

Графическое задание закона распределения представлено на рис.6.1.

Рис. 6.1.

Способ описания распределения случайной величины в виде таблицы, в виде формулы или графически применим только для дискретных случайных величин.

Интегральная функция распределения позволяет задать как дискретную, так и непрерывную случайную величину.

Интегральная функция распределения (ИФР)– это функция F(x), определяющая для каждого возможного значения x вероятность того, что случайная величина X примет значение меньшее x, т. е.

Геометрический смысл интегральной функции распределения – это вероятность того, что случайная величина X примет значение, которое на числовой оси лежит левее точки x.

Свойства интегральной функции распределения:

Значения интегральной функции распределения принадлежат отрезку [0;1]: .
Вероятность того, что случайная величина X примет значение, заключенной в интервале (a,b), равна приращению интегральной функции распределения на этом интервале

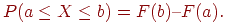
Если все возможные значения x случайной величины принадлежат интервалу (a, b), то

, если

График ИФР непрерывной случайной величины представлен на рис. 6.2

Рис. 6.2. График ИФР непрерывной случайной величины

График ИФР дискретной случайной величины представлен на рис. 6.3

Рис. 6.3. График ИФР дискретной случайной величины

Для описания распределения вероятностей непрерывной случайной величины используется дифференциальная функция распределения.

Дифференциальная функция распределения (ДФР) (или плотность вероятности) – это первая производная от интегральной функции.

Интегральная функция распределения является первообразной для дифференциальной функции распределения. Тогда

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:

Геометрический смысл ДФР состоит в следующем: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью x, кривой распределения f(x) и прямыми x = a и x = b (рис. 6.4).

Рис. 6.4.

График дифференциальной функции распределения принято называть кривой распределения.

Свойства дифференциальной функции распределения:

Дифференциальная функция распределения неотрицательна, т. е.
Если все возможные значения случайной величины принадлежат интервалу (a, b), то

Так как дифференциальная функция распределения равна f(x)=F’(x), то можно записать

(6.1)

т. е. предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу к длине этого интервала (при ), равен значению дифференциальной функции распределения в точке x.

Аналогичное (6.1) определение дается в механике для определения плотности массы в точке (если масса распределена вдоль оси X по закону F(x)), поэтому в теории вероятности для дифференциальной функции распределения f(x) часто используется термин "плотность вероятности в точке".

На основании (6.1) запишем:

(6.2)

Вероятностный смысл дифференциальной функции распределения на основании (6.2) таков: вероятность того, что случайная величина примет значение принадлежащее интервалу приближенно равна произведению плотности вероятности в точке x на длину интервала или (на графике) площади прямоугольника с основанием и высотой f(x).

Дифференциальную функцию распределения часто называют законом распределения вероятностей непрерывных случайных величин.

При решении прикладных задач сталкиваются с различными законами распределения вероятностей непрерывных случайных величин. Часто встречаются законы равномерного и нормального распределения.

Примечание. Отметим, что законом распределения вероятностей дискретных случайных величин, называют соответствие между возможными значениями дискретной случайной величины и вероятностями их появления. Вероятности можно задать таблично, аналитически (биномиальное распределение по формуле Бернулли, распределение Пуассона) или графически (в виде многоугольника распределения).

Закон равномерного распределения вероятностей непрерывной случайной величины используется при имитационном моделировании сложных систем на ЭВМ как первоначальная основа для получения всех необходимых статистических моделей. При этом, если специально не оговорен закон распределения случайных чисел, то имеют ввиду равномерное распределение.

Распределение вероятностей называют равномерным, если на интервале (a,b), которому принадлежат все возможные значения случайной величины, дифференциальная функция распределения имеет постоянное значение, т. е. f(x) = C.

Так как

то

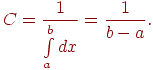
Отсюда закон равномерного распределения аналитически можно записать так:

График дифференциальной функции равномерного распределения вероятностей представлен на рис. 6.5

Рис. 6.5.

Интегральную функцию равномерного распределения аналитически можно записать так:

График интегральной функции равномерного распределения вероятностей представлен на рис. 6.6

Рис. 6.6.

Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходиться пользоваться, так называемыми, числовыми характеристиками случайной величины. К ним относятся:

Математическое ожидание M,
Дисперсия D,
Среднее квадратичное отклонение .

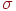Математическое ожидание дискретной случайной величины X – это сумма произведений всех ее возможных значений на их вероятности .

(6.3)

Математическое ожидание непрерывной случайной величины X, возможное значение которой принадлежит отрезку [a,b] – это определенный интеграл

(6.4)

Последнее определение (для непрерывной случайной величины) получено на основании того, что вероятность попадания X в интервал приблизительно равна .

Математическое ожидание случайной величины (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина. Она характеризует среднее значение случайной величины.

Свойства математического ожидания:

M(C)=C – математическое ожидание константы равно самой константе
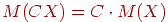
M(X+Y)=M(X)+M(Y)

Вероятностный смысл математического ожидания:

Математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины:

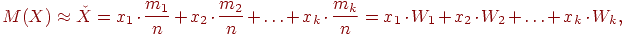
где:

m_k– частота наблюдений, W_k– относительная частота.

Дисперсия и среднее квадратичное отклонение – это числовые характеристики случайной величины, которые позволяют оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания.

Отклонением называют разность между значением случайной величины и ее математическим ожиданием, т. е.

x_I - M(X).

Пусть закон распределения дискретной случайной величины известен:

X x₁ x₂ … x_nP p₁ p₂ … p_n

Тогда закон распределения отклонения этой случайной величины имеет вид:

X-M(X) x₁-M(X) x₂-M(X) … x_n-M(X) P p₁ p₂ … p_n

Так как одни возможные отклонения положительны, а другие отрицательны, то математическое ожидание отклонения обладает важным свойством:

M(X – M(X))=0,

т.е. математическое ожидание отклонения всегда равно нулю.

Поэтому для оценки рассеяния случайной величины вокруг ее математического ожидания вычисляют квадрат отклонения случайной величины, т. е.

(x_i - M (X))².

Дисперсией (рассеянием) случайной величины (как дискретной, так и непрерывной) называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Для дискретной случайной величины:D(X) = M(X – M(X))²

Для непрерывной случайной величины:

В последнем выражении все возможные значения случайной величины принадлежат отрезку (a, b).

Дисперсия случайной величины (как дискретной, так и случайной) есть неслучайная (постоянная величина).

Пример:

Дискретная случайная величина имеет следующий закон распределения:

X 1 2 5P 0.3 0.5 0.2

Математическое ожидание этой случайной величины:

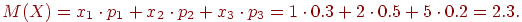
Квадраты отклонений возможных значений случайной величины:

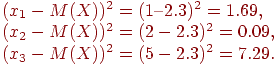
Закон распределения квадрата отклонения:

(x-M(X))² 1.69 0.09 7.29p 0.3 0.5 0.2

Тогда дисперсия приведенной случайной величины равна:

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии, т. е.

В приведенном примере среднее квадратичное отклонение случайной величины равно:

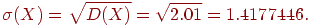
Для вычисления дисперсии часто бывает удобно пользоваться следующей формулой: D(X)=M(X²)–(M(X))², т. е. дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.

Рассмотрим еще раз предыдущий пример.

Дискретная случайная величина задана законом распределения:

X 1 2 5P 0.3 0.5 0.2

Математическое ожидание этой случайной величины равно:

Закон распределения квадрата случайной величины, т. е. X²:

X² 1 4 25P 0.3 0.5 0.2

Математическое ожидание X² равно:

Тогда дисперсия приведенной случайной величины равна:

Среднее квадратичное отклонение:

Рассмотрим пример, если задана непрерывная случайная величина.

Пусть непрерывная случайная величина задана интегральной функцией распределения:

Найдем дифференциальную функцию распределения:

Математическое ожидание X и X²:

Тогда:

Если равномерно распределенная случайная величина задана в интервале [a,b], то ее математическое ожидание, дисперсия и среднее квадратичное отклонение равны:

Свойства дисперсии:

D(C)=0
D(CX)=C²D(X)
D(X+Y)=D(X)+D(Y),
D(C+X)=D(X),
D(X-Y)=D(X)+D(Y).

Свойство среднеквадратичного отклонения:

Закон нормального распределения вероятностей непрерывной случайной величины занимает особое место среди различных теоретических законов, т. к. является основным во многих практических исследованиях, им описывается большинство случайных явлений, связанных с производственными процессами.

К случайным явлениям, подчиняющимся нормальному закону распределения, относятся ошибки измерений производственных параметров, распределение технологических погрешностей изготовления, рост и вес большинства биологических объектов, распределение параметров пленочных резисторов и др.

Нормальным называют закон распределения вероятностей непрерывной случайной величины, который описывается дифференциальной функцией

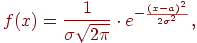
(6.5)

где

a - математическое ожидание случайной величины;

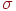-среднее квадратичное отклонение нормального распределения.

График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса) (рис. 6.7).

Рис. 6.7.

Свойства нормальной кривой (кривой Гаусса):

Кривая симметрична относительно прямой x = a.
Нормальная кривая расположена над осью X, т. е. при всех значениях X функция f(x) всегда положительна.
Ось X является горизонтальной асимптотой графика, т. к.

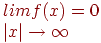
При x = a функция f(x) имеет максимум равный

В точках A и B пр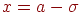и и кривая имеет точки перегиба, ординаты которых равны.

При этом, вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит среднего квадратичного отклонения , равна 0,6826.

В точках E и G, при и , значение функции f(x) равно

а вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит удвоенного среднего квадратичного отклонения, равна 0,9544.

Асимптотически приближаясь к оси абсцисс, кривая Гаусса в точках C и D, при и , очень близко подходит к оси абсцисс. В этих точках значение функции f(x) очень мало

а вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит утроенного среднего квадратичного отклонения, равна 0,9973. Это свойство кривой Гаусса называется "правило трех сигм".

Изменение величины параметра a (математического ожидания случайной величины) не изменяет форму нормальной кривой, а приводит лишь к ее смещению вдоль оси X: вправо, если a возрастает, и влево, если a убывает.

При a=0 нормальная кривая симметрична относительно оси ординат.

Изменение величины параметра 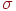(среднего квадратичного отклонения) изменяет форму нормальной кривой: с возрастанием 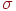ординаты нормальной кривой убывают, кривая растягивается вдоль оси X и прижимается к ней. При убывании 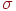ординаты нормальной кривой увеличиваются, кривая сжимается вдоль оси X и становится более "островершинной".

При этом, при любых значениях и 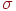площадь ограниченная нормальной кривой и осью X, остается равной единице (т. е. вероятность того, что случайная величина, распределенная нормально, примет значение ограниченное на оси X нормальной кривой, равна 1).

Нормальное распределение с произвольными параметрами и 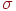, т. е. описываемое дифференциальной функцией

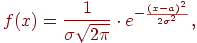
называется общим нормальным распределением.

Нормальное распределение с параметрами и , т. е. описываемое дифференциальной функцией

(6.6)

называется нормированным распределением (рис. 6.8). В нормированном распределении дифференциальная функция распределения равна:

Рис. 6.8.

Интегральная функция общего нормального распределения имеет вид:

(6.7)

Интегральная функция нормированного распределения имеет вид:

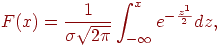
(6.8)

где

Пусть случайная величина X распределена по нормальному закону в интервале (c, d). Тогда вероятность того, что X примет значение, принадлежащее интервалу (c, d) равна

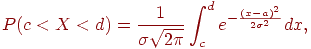
Пронормируем это выражение. Для этого введем новую переменную z

Откуда:

Новые пределы интегрирования:

Для

для

Тогда, после нормирования, вероятность того, что случайная величина X примет значение, принадлежащее интервалу (c, d) равна

Пользуясь функцией Лапласа (функция табулирована)

окончательно получим

Пример.

Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратичное отклонение этой случайной величины равны a=30 и . Найти вероятность того, что X примет значение в интервале (10, 50).

Решение:

По условию: .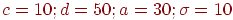

Тогда

Пользуясь готовыми таблицами Лапласа, имеем:

Отсюда

Лекция: Метод Монте-Карло

Лекция рассматривает проблемы получения (генерирования) на ЭВМ случайных числовых последовательностей с заданными вероятностными характеристиками при построении математических моделей.

При реализации на ЭВМ статистического моделирования возникает задача получения (генерирования) на ЭВМ случайных числовых последовательностей с заданными вероятностными характеристиками, в которых каждое число – это имитация случайного значения какого-либо параметра реального процесса или системы, подверженного случайным возмущениям.

Генерирование на ЭВМ таких случайных числовых последовательностей получило название "метод Монте-Карло".

В математической литературе часто используется термины "последовательность случайных чисел" или просто "случайные числа".

Однако, если проанализировать эти термины с философской точки зрения, то можно спросить: а есть ли такой объект как случайное число? Число 2 – это случайное число? Или число 17 – это случайное число? Конечно, нет. Если использовать точные термины, то можно говорить только о случайной последовательности чисел или о случайном значении параметров. Однако, в литературе широко используется термины "случайные числа" и "последовательность случайных чисел", и это означает, что каждое число было получено самым произвольным образом, без всякой связи с другими членами последовательности, и что у него есть определенная вероятность оказаться в заданном интервале.

Раньше ученые, нуждавшиеся для своей работы в случайных числах, раскладывали карты, бросали кости или вытаскивали шары из урны, которую предварительно как следует трясли. В 1927 году Л. Типпетт опубликовал таблицы, содержащие свыше 40 000 случайных чисел, взятых произвольно из отчетов по переписи. Позже были сконструированы специальные машины, механически вырабатывающие случайные числа. В 1955 году компания RAND Corporation опубликовала хорошо известные таблицы с миллионом случайных чисел, полученных одной из таких машин.

После создания ЭВМ начались поиски эффективных алгоритмов получения (генерирования на ЭВМ) последовательностей случайных чисел, пригодных для программной реализации.

Последовательности случайных чисел, вырабатываемые детерминистскими способами (т. е. с помощью специальных алгоритмов) называются псевдослучайными или квазислучайными. В дальнейшем мы будем их называть просто случайными последовательностями, понимая, что они просто производят впечатление случайных.

Задачу генерирования случайных чисел на ЭВМ с заданным законом распределения решают в несколько этапов:

Вначале получают последовательность равномерно распределенных на интервале [0, 1] псевдослучайных чисел.

Из равномерно распределенной последовательности получают последовательность псевдослучайных чисел с заданным законом распределения в заданном интервале.

Равномерным называется такое распределение, при котором каждое возможное случайное число равновероятно. Обычно, если специально не оговорен закон распределения случайных чисел, то обычно имеют в виду равномерное распределение.

Сущность алгоритмических методов получения равномерно распределенных псевдослучайных чисел заключается в том, что псевдослучайные числа получают с помощью некоторой рекуррентной формулы x_i+1 = f (x_i),

где каждое следующее(i+1)-e значение образуется из предыдущего (или группы предыдущих) путем применения некоторого алгоритма, содержащего логические и арифметические операции.

Известно большое количество имитации равномерного распределения (методы вычетов, суммирования, усечения, перемешивания). Общими для всех этих методов являются требования:

Количество операций для получения каждого псевдослучайного числа должно быть минимальным;
Случайные числа генерируются как можно менее коррелированными, а их распределение – близким к равномерному

Метод середины квадрата

Первым алгоритмический метод получения равномерно распределенных псевдослучайных чисел предложил Джон фон Нейман (один из основоположников кибернетики). Метод получил название "метод середины квадрата".

Суть метода: предыдущее случайное число возводится в квадрат, а затем из результата извлекаются средние цифры.

Например:

и т.д.

Как видно метод середины квадрата довольно хорошо должен "перемешивать" предыдущее число. Однако он имеет недостатки:

Если какой-нибудь член последовательности окажется равным нулю, то все последующие члены также будут нулями.
Последовательности имеют тенденцию "зацикливаться", т. е. в конце концов, образуют цикл, который повторяется бесконечное число раз.

Свойство "зацикливаться" присуще всем последовательностям, построенных по рекуррентной формуле x_i+1=f(x_i).

Повторяющийся цикл называется периодом. Длина периода у различных последовательностей разная. Чем больше, тем лучше.