Оказывается, амплитуду синусоидального сигнала, а также любого другого сигнала, можно оценивать не только как абсолютное максимальное его значение. Иногда пользуются понятием двойная амплитуда (амплитуда от пика до пика сигнала), которая, как нетрудно догадаться, равна удвоенной амплитуде. Иногда употребляют понятие эффективное значение, которое определяется следующим образом: U эфф = (1/√2) А = 0,101 А или 2 А / Uэфф = 2√2 (это соотношение справедливо только для синусоидальных сигналов: для других видов сигналов отношение двойной амплитуды к эффективному значению будет другим). Пусть вас не удивляет, что сигнал часто характеризуется эффективным значением; дело в том, что именно эффективное значение используется для определения мощности. В США напряжение в сети имеет эффективное значение 117 В и частоту 60 Гц. Амплитуда этого напряжения равна 165 В (двойная амплитуда составляет 330 В).
Изменение амплитуды в децибелах. Как сравнить амплитуды двух сигналов? Можно, например, сказать, что сигнал X в два раза больше, чем сигнал Y. Во многих случаях именно так и производят сравнение. Но очень часто подобные отношения достигают миллионов, и тогда удобнее пользоваться логарифмической зависимостью и измерять отношение в децибелах (децибел составляет одну десятую часть бела, но единицей «бел» никогда не пользуются). По определению отношение двух сигналов, выраженное в децибелах, это дБ = 20·lg(A2 / A1), где А 1 и А 2 – амплитуды двух сигналов.
Например, если один сигнал имеет амплитуду вдвое большую, чем другой, то отношение первого сигнала ко второму составляет +6 дБ, так как lg2 = 0,3010. Если один сигнал в 10 раз больше другого, то отношение первого ко второму составляет +20 дБ, а если один сигнал в 10 раз меньше другого ‑ то ‑20 дБ. Отношение мощностей двух сигналов определяется так:
дБ = 10·lg(P2 / P1),
где Р 1 и Р2 – мощности двух сигналов.
Если оба сигнала имеют одну и ту же форму, т. е. представлены синусоидами, то оба способа определения отношения сигналов (через амплитуду и мощность) дают одинаковый результат. Для сравнения сигналов разной формы, например, синусоидального и шумового следует использовать мощность (или эффективные значения).
Хотя децибел служит для определения отношения двух сигналов, иногда эту единицу используют для измерения абсолютного, а не относительного значения амплитуды. Дело в том, что можно взять некоторую эталонную амплитуду и определять любую другую амплитуду в децибелах по отношению к эталонной.
Известно несколько стандартных значений амплитуды, используемых для такого сравнения (эти значения не указываются, но подразумеваются); приведем некоторые из них: а) дБВ – эффективное значение 1 В; б) дБВт – напряжение, соответствующее мощности 1 мВт на некоторой предполагаемой нагрузке, для радиочастот это обычно 50 Ом, для звуковых частот – 600 Ом (напряжение 0 дБВт на этих нагрузках имеет эффективное значение 0,22 В и 0,78 В); в) дБп – небольшой шумовой сигнал, генерируемый резистором при комнатной температуре (об этом более подробно пойдет речь в разд. 7.11).
Помимо перечисленных существуют эталонные сигналы для измерений в других областях. Например, в акустике уровень звукового давления 0 дБ соответствует сигналу, среднее квадратурное давление которого составляет 0,0002 мкбар (1 бар равен 106 дин на квадратный сантиметр или приблизительно 1 атмосфере); в связи уровни определяются в дБС (относительный шум в полосе частот с весовой функцией С). Обращаем ваше внимание на эталонную амплитуду 0 дБ: пользуясь этим значением, не забывайте его оговорить, например «амплитуда 27 дБ относительно эффективного значения 1 В», или в сокращенной форме «27 дБ относительно 1 Вэфф», или пользуйтесь условным обозначением дБВ.
Упражнение 1.11. Отношение двух сигналов составляет: а) 3 дБ, б) 6 дБ, в) 10 дБ, г) 20 дБ. Для каждого случая определите отношение напряжений и мощностей сигналов.
Другие типы сигналов
Линейно‑меняющийся сигнал. Линейно‑меняющийся сигнал (показан на рис. 1.18) – это напряжение, возрастающее (или убывающее) с постоянной скоростью. Это напряжение, конечно, не может расти бесконечно. Поэтому обычно такое напряжение имеет вид, показанный на графике рис. 1.19, ‑ напряжение нарастает до конечного значения, или на графике рис. 1.20 – пилообразное напряжение.
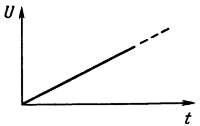
Рис. 1.18. Напряжение в виде линейно‑меняющегося сигнала.
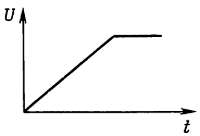
Рис. 1.19. Ограниченный линейно‑меняющийся сигнал.
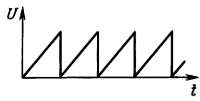
Рис. 1.20. Пилообразный сигнал.
Треугольный сигнал. Треугольный сигнал приходится «ближайшим родственником» линейно‑меняющемуся сигналу; отличие состоит в том, что график треугольного сигнала является симметричным (рис. 1.21).
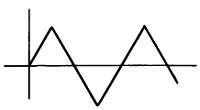
Рис. 1.21. Треугольный сигнал.
Сигналы шумов. Сигналы, о которых пойдет речь, очень часто смешивают с шумами, имея в виду только тепловые случайные шумы. Шумовые напряжения характеризуются частотным спектром (произведение мощности на частоту в герцах) и распределением амплитуд. Одним из наиболее распространенных типов шумовых сигналов является белый шум с гауссовым распределением в ограниченном спектре частот. Для такого сигнала произведение мощности на частоту в герцах сохраняется постоянным в некотором диапазоне частот, а вариации амплитуды для большого числа измерений мгновенного значения описываются распределением Гаусса. Шумовой сигнал такого типа генерирует резистор (шум Джонсона), и он создает неприятности при всевозможных измерениях, в которых требуется высокая чувствительность. На экране осциллографа мы видим шумовой сигнал таким, как он показан на рис. 1.22.
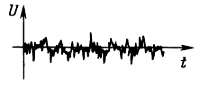
Рис. 1.22. Шумовой сигнал.
Более подробно шумовые сигналы и способы борьбы с шумовыми помехами будут рассмотрены в гл. 7. В разд. 9.32‑9.35 рассматриваются вопросы генерации шумовых сигналов.
Прямоугольные сигналы. График изменения прямоугольного сигнала во времени показан на рис. 1.23. Как и синусоидальный, прямоугольный сигнал характеризуется амплитудой и частотой. Если на вход линейной схемы подать прямоугольный сигнал, то сигнал на выходе вряд ли будет иметь прямоугольную форму. Для прямоугольного сигнала эффективное значение равно просто амплитуде.
Форма реального прямоугольного сигнала отличается от идеального прямоугольника; обычно в электронной схеме время нарастания сигнала tн составляет от нескольких наносекунд до нескольких микросекунд. На рис. 1.24 показано, как обычно выглядит скачок прямоугольного сигнала. Время нарастания определяется как время, в течение которого сигнал нарастает от 10 до 90 % своей максимальной амплитуды.
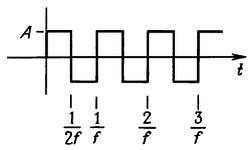
Рис. 1.23. Прямоугольные сигналы.
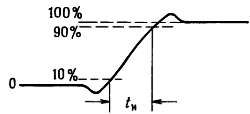
Рис. 1.24. Время нарастания скачка прямоугольного сигнала.
Импульсы. Импульсы – это сигналы, показанные на рис. 1.25. Они характеризуются амплитудой и длительностью импульса. Если генерировать периодическую последовательность импульсов, то можно говорить о частоте, или скорости повторения импульса, и о «рабочем цикле», равном отношению длительности импульса к периоду повторения (рабочий цикл лежит в пределах от 0 до 100 %).
Импульсы могут иметь положительную или отрицательную полярность (пьедестал), кроме того, они могут быть нарастающими или спадающими. Например, второй импульс, показанный на рис. 1.25, является убывающим импульсом положительной полярности (или спадающим импульсом с положительным пьедесталом).
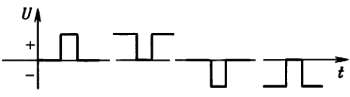
Рис. 1.25. Нарастающие и убывающие импульсы обоих полярностей.
Сигналы в виде скачков и пиков. Сигналы в виде скачков и пиков упоминаются часто, но широкого применения не находят. К их помощи прибегают для описания работы схем. Если попытаться их нарисовать, то они будут выглядеть так, как показано на рис. 1.26. Скачок представляет собой часть прямоугольного сигнала, а пик – это два скачка, следующие с очень коротким интервалом.
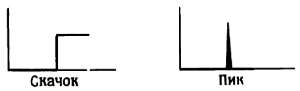
Рис. 1.26.
Логические уровни
Импульсы и прямоугольные сигналы широко используются в цифровой электронике. В цифровой схеме состояние любой точки в любой момент времени определяют заранее известные уровни напряжения. Эти уровни называют просто «ВЫСОКИЙ» и «НИЗКИЙ». Они соответствуют значениям «ложь» (0) и «истина» (1) булевой алгебры логики, которая имеет дело с переменными, принимающими эти значения.
В цифровой электронике точные значения напряжений не играют роли. Задача состоит в том, чтобы различать только уровни напряжения. В связи с этим для каждого семейства цифровых логических элементов определены допустимые значения высокого и низкого уровня напряжения. Например, логическое семейство цифровых элементов «74НС» работает от напряжения +5 В, при этом выходные уровни составляют 0 В (низкий уровень) и 5 В (высокий уровень), а порог срабатывания на входе равен 2,5 В. Реальные значения выходного напряжения могут составлять 1 В относительно «земли» или +5 В, но без учета ложного срабатывания. О логических уровнях речь пойдет дальше, в гл. 8–9.
Источники сигналов
Нередко источник сигнала входит как неотъемлемая часть в саму схему. Но для испытательного режима работы очень удобен отдельный независимый источник сигнала. В качестве такого источника могут выступать три типа приборов: генераторы (синусоидальных) сигналов, генераторы импульсов и генераторы функций (сигналов специальной формы).
Генераторы (синусоидальных) сигналов. Генераторами сигналов называют генераторы синусоидальных колебаний, которые обычно обеспечивают широкий диапазон частот (как правило, от 50 кГц до 50 МГц) и приспособлены для «тонкой» регулировки амплитуды (для этой цели используется схема резистивного делителя, называемого аттенюатором). В некоторых генераторах предусмотрена возможность модуляции выходного сигнала (см. гл. 13). Одной из разновидностей генератора сигнала является свип‑генератор (генератор качающейся частоты) – он может периодически производить развертку выходной частоты в некотором диапазоне частот. Это качество прибора очень полезно при испытаниях схем, свойства которых определенным образом зависят от частоты (например, резонансные схемы или фильтры). В наши дни эти и многие другие приборы выпускаются в исполнении, позволяющем задавать (программировать) частоту, амплитуду и другие параметры с помощью вычислительной машины или другого цифрового устройства.
Еще одной разновидностью генераторов сигналов является синтезатор частот – устройство, которое позволяет производить точную установку частоты генерируемых синусоидальных колебаний. Частота задается цифровым способом, часто с точностью до восьми или более знаков после запятой, и синтезируется с помощью точного эталона кварцевого генератора цифровыми методами, о которых речь пойдет позже (в разд. 9.27‑9.31). Если перед вами когда‑нибудь будет стоять задача получения сигнала с абсолютно достоверным, точным значением частоты, то без синтезатора ее не решить.
Генераторы импульсов. Генераторы импульсов всего лишь формируют импульсы, но как совершенно они выполняют свою задачу. В них предусмотрена возможность регулировки ширины (длительности) импульса, частоты повторения, амплитуды, времени нарастания и других параметров. Кроме того, многие генераторы позволяют генерировать пары импульсов с заданными интервалами и частотой повторения и даже кодовые последовательности импульсов. В большинстве современных генераторов импульсов предусмотрены логические выходы, обеспечивающие легкое сопряжение с цифровыми схемами. Как и в генераторах синусоидальных сигналов, в генераторах импульсов часто предусмотрено внешнее программирование.
Генераторы функций (специальных сигналов). Во многих отношениях генераторы функций являются наиболее гибкими из всех источников сигналов. Они позволяют формировать синусоидальные, треугольные, прямоугольные сигналы в очень широком диапазоне частот (от 0,01 Гц до 10 МГц), при этом предусмотрена возможность регулировки амплитуды и смещения по постоянному току (постоянное напряжение, добавляемое к сигналу). Многие генераторы функций могут производить развертку частоты, причем в нескольких режимах (линейное или логарифмическое изменение частоты во времени). Промышленность выпускает генераторы функций с импульсным выходом (правда, они не обладают гибкостью генераторов импульсов) и возможностью модуляции выходного сигнала.
Промышленность выпускает также программируемые и цифровые генераторы функций. В цифровых генераторах значение частоты (а иногда и амплитуды) считывается в цифровом виде. В последние годы семейство генераторов функции пополнилось синтезирующим генератором функции (генератором‑синтезатором функций) – устройством, которое сочетает в себе гибкость генератора функций со стабильностью и точностью синтезатора частот. Примером служит генератор типа HP 8116А, который формирует синусоидальные, прямоугольные и треугольные сигналы (а также импульсы, линейно‑меняющиеся сигналы, сигналы, изменяющиеся как функция hav х и т. д.), в диапазоне частот от 0,001 Гц до 50 МГц.
Частота и амплитуда (от 10 мВ до 16 В от пика до пика) задаются программно, с помощью программы определяется также линейное или логарифмическое изменение частоты во времени. Помимо всего прочего устройство может работать как триггер, логическая схема, формировать всплески, производить амплитудную, частотную, импульсную модуляцию, формировать частоту, управляемую напряжением, и одиночные циклы. И последнее: если вам хотелось бы иметь один источник сигналов на все случаи жизни, то для этой цели лучше подойдет генератор функций.






