Следующие приставки приняты для образования кратных и дольных единиц измерения в научной и инженерной практике:

При сокращенном обозначении дольных единиц измерения соответствующая приставка и условное обозначение единицы пишутся слитно. Обратите внимание на использование прописных и строчных букв, особенно м и Μ в приставках и обозначениях единиц 1 мВт – это 1 милливатт, или тысячная доля ватта; 1 МГц – это 1 миллион герц. Полные наименования единиц измерения всегда пишутся со строчной буквы, даже если они образованы от имен собственных. Полное наименование единицы измерения с приставкой также всегда пишется со строчной буквы.
Прописные буквы используются для условных сокращений единиц измерения. Например: герц и килогерц, но Гц и кГц; ватт, милливатт и мегаватт, но Вт, мВт и МВт.
* * *
Сопротивление и резисторы. Интересно, что ток, протекающий через металлический проводник (или другой материал, обладающий некоторой проводимостью), пропорционален напряжению, приложенному к проводнику. (Что касается провода, который используется в качестве проводников в схемах, то его обычно берут достаточно большого сечения, чтобы можно было пренебречь падениями напряжения, о которых мы говорили выше.) Это ни в коем случае не обязательно для всех случаев жизни. Например, ток, протекающий через неоновую лампу, представляет собой нелинейную функцию от приложенного напряжения (он сохраняет нулевое значение до критического значения напряжения, а в критической точке резко возрастает). То же самое можно сказать и о целой группе других элементов – диодах, транзисторах, лампах и др. Если вас интересует, почему металлические проводники ведут себя именно так, советуем прочитать курс физики Berkeley Physics Course, том II, разд. 4.3–4.7 (см. библиографию). Резисторы изготавливают из проводящего материала (графита, тонкой металлической или графитовой пленки или провода, обладающего невысокой проводимостью). К каждому концу резистора прикреплен провод.
Резистор характеризуется величиной сопротивления
R = U / I;
сопротивление R измеряется в омах, если напряжение U выражено в вольтах, а ток I в амперах. Это соотношение носит название «закон Ома». Резисторы наиболее распространенного типа – углеродистые композиционные – имеют сопротивление от 1 ома (1 Ом) до 22 мегаом (22 МОм).
Резисторы характеризуются также мощностью, которую они рассеивают в пространство (наиболее распространены резисторы с мощностью рассеяния 1/4 Вт) и такими параметрами, как допуск (точность), температурный коэффициент, уровень шума, коэффициент напряжения (показывающий, в какой степени сопротивление зависит от приложенного напряжения), стабильность во времени, индуктивность и пр. Более подробную информацию о резисторах содержит разд. «Резисторы», напечатанный мелким шрифтом, а также приложения Б и Г в конце второго тома.
Грубо говоря, резисторы используются для преобразования напряжения в ток и наоборот. Этот вывод может показаться банальным, но скоро вы поймете, что имеется в виду.
Последовательное и параллельное соединение резисторов. Из определения сопротивления следует несколько выводов:
1. Сопротивление двух последовательно соединенных резисторов (рис. 1.3) равно:
R = R1 + R2.

Рис. 1.3.
При последовательном соединении резисторов всегда получаем большее сопротивление, чем сопротивление отдельного резистора.
2. Сопротивление двух параллельно соединенных резисторов (рис. 1.4) равно
R = R1R2 /(R1 + R2) или R = 1/(1/ R1 + 1/ R2).

Рис. 1.4.
При параллельном соединении резисторов всегда получаем меньшее сопротивление, чем соединение отдельных резисторов. Сопротивление измеряется в омах (Ом). На практике, когда речь идет о резисторах с сопротивлением более 1000 Ом (1 кОм), иногда оставляют только приставку, опуская в обозначении «Ом», т. е. резистор с сопротивлением 10 кОм иногда обозначают как 10 К, а резистор с сопротивлением 1 МОм – как 1 М. На схемах иногда опускают и обозначение «Ом», оставляя только число. Может быть, все это кажется вам не очень интересным? Немного терпения, и мы перейдем к интересным практическим примерам.
* * *
РЕЗИСТОРЫ
Резисторы поистине вездесущи. Типы резисторов почти столь же многочисленны, как и схемы, в которых они применяются. Резисторы используются в усилителях, в качестве нагрузки для активных устройств, в схемах смещения и в качестве элементов обратной связи. Вместе с конденсаторами они используются для задания постоянной времени и работают как фильтры. Они служат для установки величин рабочих токов и уровней сигналов. В схемах питания резисторы используются для уменьшения напряжения за счет рассеяния мощности, для измерения токов и для разряда конденсаторов после снятия питания. В прецизионных схемах они помогают устанавливать нужные токи, обеспечивать точные коэффициенты пропорциональности для напряжения, устанавливать точные коэффициенты усиления. В логических схемах резисторы выступают в качестве конечных элементов линий и шин, «повышающих» и «понижающих» элементов. В высоковольтных схемах резисторы служат для измерения напряжений, для выравнивания токов утечки через диоды или конденсаторы, соединенные последовательно. На радиочастотах они используются даже в качестве индуктивностей.
Промышленность выпускает резисторы с сопротивлением от 0,01 Ом до 1012 Ом и мощностью от 1/8 до 250 Вт с допуском от 0,005 до 20 %. Резисторы изготавливают из графитовых смесей, металлических пленок, проводов, накрученных на каркас, или на основе полупроводниковых элементов, подобных полевым транзисторам. Наиболее распространены углеродистые композиционные резисторы, имеющие мощность 1/4 или 1/2 Вт. Существует стандартный диапазон значений сопротивлений ‑ от 1 Ом до 100 МОм, причем для резисторов с допуском на сопротивление, равным 5 %, выпускается в два раза больше значений сопротивлений, чем для резисторов с допуском 10 % (см. приложение В). Мы рекомендуем использовать резисторы фирмы Allen Bradley типа AB (1/4 Вт, 5 %), так как они имеют понятную маркировку, стабильные характеристики и надежное соединение с проводниками выводов.
Резисторы настолько просты в обращении, что очень часто их принимают как нечто само собой разумеющееся. Между тем они не идеальны, и стоит обратить внимание на некоторые их недостатки.
Возьмем, например, получившие широкое распространение резисторы композиционного типа с допуском 5 %. Они хороши почти для любых схем с некритичными параметрами, но невысокая стабильность этих резисторов не позволяет использовать их в прецизионных схемах. Следует помнить об ограничениях, свойственных этим элементам, чтобы в один прекрасный день не оказаться разачарованным.
Основной недостаток состоит в изменении сопротивления во времени под действием температуры, напряжения, влажности. Другие недостатки связаны с индуктивными свойствами (они существенно сказываются на высоких частотах), с наличием термальных точек в мощных схемах или шумов в усилителях с низким уровнем шума. Ниже приводятся параметры резисторов в самых жестких условиях эксплуатации; обычно условия бывают лучше, но правильнее рассчитывать на худшее.
ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ ФИРМЫ ALLEN BRADLEY, (СЕРИЯ АВ, ТИП СВ)
Стандартный допуск в номинальных условиях составляет 5 %. Максимальная мощность при температуре окружающей среды 70 °C составляет 0,25 Вт, при этом внутренняя температура повышается до 150 °C. Максимальное приложенное напряжение составляет (0,25 R)1/2 или 250 В (меньшее из двух значений).
И это на самом деле так! (см. рис. 6.53). Однократное превышение напряжения до 400 В в течение 5 с вызывает необратимое изменение сопротивления на 2 %.

В схемах, где требуется высокая точность или стабильность, следует использовать резисторы из металлической пленки с допуском 1 % (см. приложение Г). Они обеспечивают стабильность не хуже 0,1 % в нормальных условиях и не хуже 1 % в самых жестких условиях. Прецизионные проволочные резисторы способны удовлетворить наиболее высоким требованиям.
Если ожидается, что мощность, рассеиваемая в схеме, будет составлять более 0,1 Вт, то следует выбрать резистор с большим значением рассеиваемой мощности. Композиционные углеродистые резисторы характеризуются мощностью до 2 Вт, а мощные проволочные резисторы ‑ более высокими значениями.
Для мощных схем наилучшие характеристики обеспечивает резистор с отводом тепла. Резисторы этого типа выпускаются с допуском 1 % и могут надежно работать при собственной температуре до 250 °C в течение длительного периода времени. Допустимая рассеиваемая мощность зависит от воздушного потока, температурных условий на выводах и плотности схемы; следовательно, мощность на резисторе следует рассматривать как грубую ориентировочную величину. Отметим также, что мощность резистора связана со средним значением мощности, рассеиваемой в схеме, и может существенно превышаться в короткие интервалы времени (в зависимости от «тепловой массы» эти интервалы могут длиться несколько секунд или более).
Упражнение 1.1. Возьмем два резистора сопротивлением 5 и 10 кОм. Чему равно сопротивление при (а) последовательном и (б) параллельном их соединении?
Упражнение 1.2. Какую мощность будет рассеивать в пространство резистор с сопротивлением 1 Ом, подключенный к батарее автомобиля с напряжением 1 В?
Упражнение 1.3. Докажите справедливость формул для сопротивления последовательного и параллельного соединения резисторов.
Упражнение 1.4. Покажите, что сопротивление нескольких параллельно соединенных резисторов определяется следующим образом:

* * *
Секрет резисторов, соединенных параллельно: начинающие часто приступают к сложным алгебраическим выкладкам или углубляются в законы электроники, а здесь как раз лучше всего воспользоваться интуитивным правилом.
Приступим теперь к освоению интуитивных правил и развитию интуиции.
Правило 1. Сопротивление двух резисторов, один из которых обладает большим сопротивлением, а другой малым, соединенных между собой последовательно (параллельно), приблизительно равно большему (меньшему) из двух сопротивлений.
Правило 2. Допустим, вы хотите узнать, чему равно сопротивление двух параллельно соединенных резисторов, обладающих сопротивлением 5 и 10 кОм. Если вообразить, что резистор сопротивлением 5 кОм представляет собой параллельное соединение двух резисторов сопротивлением 10 кОм, то схема будет представлена параллельным соединением трех резисторов с сопротивлением 10 кОм. Так как сопротивление одинаковых параллельно соединенных резисторов равно 1/ n ‑й части сопротивления одного из них, то ответ в нашей задаче будет 10 кОм/3, или 3,33 кОм. Это правило полезно усвоить, так как с его помощью можно быстро проанализировать схему «в уме».
Мы хотим, чтобы вы научились решать стоящие перед вами задачи, имея под рукой минимум – оборотную сторону почтового конверта и ручку. Тогда блестящие идеи, возникшие у вас в любой момент, не будут встречать препятствий на пути своего развития.
И еще несколько принципов нашей доморощенной философии: среди начинающих наблюдается тенденция вычислять значения сопротивлений резисторов и характеристики других компонентов схем с большой точностью, доступность же карманных калькуляторов в наше время помогает развитию этой тенденции.
Поддаваться ей не следует по двум причинам: во‑первых, компоненты сами по себе имеют определенную конечную точность (наиболее распространенные резисторы – ± 5 %; характеристики транзисторов, например часто задаются одним‑двумя коэффициентами); во‑вторых, одним из признаков хорошей схемы является ее нечувствительность к точности величин компонентов (бывают, конечно, и исключения). И еще: вы скорее придете к интуитивному пониманию схем, если разовьете в себе способность быстро прикидывать «в уме», а не будете увлекаться вычислениями с ненужной точностью на красивых калькуляторах.
Некоторые считают, что для того чтобы скорее научиться оценивать величину сопротивления, полезно вводить понятие проводимость, G = 1/ R. Ток, протекающий через элемент с проводимостью G, к которому приложено напряжение U, определяется как I = G · U (это закон Ома).
Чем меньше сопротивление проводника, тем больше его проводимость и тем больше ток, протекающий под воздействием напряжения, приложенного между концами проводника.
С этой точки зрения формула для определения сопротивления параллельно соединенных проводников вполне очевидна: если несколько резисторов или проводящих участков подключены к одному и тому же напряжению, то полный ток равен сумме токов, протекающих в отдельных ветвях. В связи с этим проводимость соединения равна сумме отдельных проводимостей составных элементов: G = G1 + G2 + G 3 +…, а это выражение эквивалентно выражению для параллельно соединенных резисторов, приведенному выше.
Инженеры неравнодушны к обратным величинам, и в качестве единицы измерения проводимости они установили 1 сименс (1 См = 1/1 Ом), который иногда называют «мо» («ом» наоборот). Хотя понятие проводимости и помогает развить интуицию в отношении сопротивления резисторов, широкого применения оно не находит, и большинство предпочитает иметь дело с величинами сопротивления, а не проводимости.
Мощность и резисторы. Мощность, рассеиваемая резистором или любым другим элементом, определяются как Ρ = U · I.
Пользуясь законом Ома, эту формулу можно записать в эквивалентном виде:
Ρ = I 2 R и Ρ = U 2/ R.
* * *
Упражнение 1.5. Возьмем схему, работающую от батареи с напряжением 15 В. Докажите, что независимо от того, как будет включен в схему резистор, обладающий сопротивлением более 1 кОм, мощность на нем не превысит 1/4 Вт.
Упражнение 1.6. Дополнительное упражнение: для Нью‑Йорка требуется 1010 Вт электрической энергии при напряжении 110 В (цифры вполне правдоподобны: 10 млн. жителей, каждый потребляет в среднем 1 кВт электроэнергии). Высоковольтный кабель может иметь диаметр 25,4 мм. Давайте подсчитаем, что произойдет, если в качестве кабеля взять провод из чистой меди диаметром 0,305 м. Сопротивление такого провода составляет 0,05 мкОм (5·10‑8 Ом) в расчете на 0,305 м. Определите: а) потери мощности в расчете на 0,305 м, исходя из того, что потери оцениваются величиной I 2 R; б) длину кабеля, на которой будут потеряны все 1010 Вт; в) если вы знаете физику, определите, до какой температуры нагреется кабель (σ = 6· 10"12 Вт/(К4·см2)).
Если расчет выполнен правильно, то результат, вероятно, удивил вас. Как же разрешить проблему?
* * *
Вход и выход. Практически во всех электронных схемах что‑либо подается на вход (обычно это напряжение) и соответственно снимается с выхода (это также чаще всего напряжение). Например, с выхода усилителя звуковой частоты снимается напряжение (оно имеет переменное значение), которое в 100 раз превышает входное напряжение (изменяющееся аналогично). В этом усилителе выходное напряжение рассматривается для данного значения напряжения, действующего на входе. Инженеры пользуются понятием передаточной функции Н, которая представляет собой отношение напряжения, измеренного на выходе, к напряжению, действующему на входе; для вышеупомянутого усилителя звуковой частоты Н – это постоянная величина (Н = 100). К изучению усилителей мы приступим в следующей главе. Однако, уже сейчас, имея представление только о резисторах, мы рассмотрим делитель напряжения (по сути он является «де‑усилителем»), который играет немаловажную роль в электронных схемах.
Делители напряжения
Мы приступаем к рассмотрению делителя напряжения, который используется в электронных схемах весьма широко. В любой настоящей схеме можно найти не меньше полдюжины делителей напряжения. Простейший делитель напряжения – это схема, которая для данного напряжения на входе создает на выходе напряжение, которое является некоторой частью входного. Простейший делитель представлен на рис. 1.5.

Рис. 1.5. Делитель напряжения. Приложенное напряжение Uвх создает на выходе напряжение Uвых (меньшее приложенного).
Что такое Uвых? Предположим здесь и далее, что нагрузки на выходе нет, тогда ток определяется следующим образом:
I = Uвх /(R1 + R2)
(Мы воспользовались формулой для определения сопротивления резистора и правилом для последовательного соединения резисторов). Тогда для R2
Uвых = I · R2 = UвхR2 /(R 1 + R2).
Обратите внимание, что выходное напряжение всегда меньше входного (или равно ему); поэтому мы говорим о делителе напряжения. Если одно из сопротивлений будет отрицательным, то можно получить усиление (т. е. выходное напряжение будет больше входного). Эта идея не так невероятна, как кажется на первый взгляд: вполне можно сделать устройство с отрицательными «приращениями» сопротивления (в качестве примера может служить туннельный диод) или просто с настоящим отрицательным сопротивлением (например, преобразователь с отрицательным импедансом, о котором мы поговорим позже). Однако эти примеры достаточно специфичны и не должны занимать сейчас ваше внимание.
Делители напряжения часто используют в схемах для того, чтобы получить заданное напряжение из большего постоянного (или переменного) напряжения.
Например, если в качестве R2 взять резистор с регулируемым сопротивлением (рис. 1.6, а), то мы получим не что иное, как схему с управляемым выходом; более простым путем комбинацию R1R2 можно получить, если у вас есть один резистор с переменным сопротивлением, или потенциометр (рис. 1.6, б).

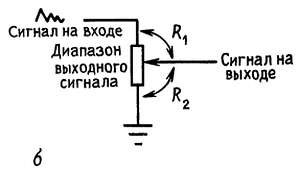
Рис. 1.6. Регулируемый делитель напряжения может состоять из двух резисторов – с фиксированным сопротивлением и с переменным сопротивлением, или из потенциометра.
Простой делитель напряжения играет важную роль и в тот момент, когда вы задумываете схему: входное напряжение и сопротивление верхней части резистора могут представлять собой, скажем, выход усилителя, а сопротивление нижней части резистора – вход последующего каскада. В этом случае, воспользовавшись уравнением для делителя напряжения, можно определить, что поступит на вход последнего каскада.
Все сказанное станет более понятным, когда чуть позже мы познакомим вас с одним интересным фактом (имеется в виду теорема об эквивалентном преобразовании схем). А сейчас немного отвлечемся от нашей темы и поговорим об источниках тока и напряжения.






