Построение уравнений Рейнольдса для сжимаемого газа поясним на примере плоской стационарной изобарической струи. Как и для несжимаемой жидкости, не будем учитывать молекулярные трение, тепловой поток и диффузию, полагая их пренебрежимо малыми по сравнению с их турбулентными аналогами.
Составим дифференциальные уравнения для математических ожиданий газодинамических комплексов:
· уравнение неразрывности
; (3.5.1)
· уравнение движения
; (3.5.2)
· уравнение энергии
; (3.5.3)
· уравнение диффузии
. (3.5.4)
Приведенные в такой записи формулы описывают турбулентные струи различных типов: дозвуковые, сверхзвуковые, изотермические, неизотермические, струи с диффузионным факелом горения.
Если, следуя подходу Рейнольдса, каждый газодинамический параметр 
представить в виде суммы среднего значения (математического ожидания) и отклонения от среднего (пульсации):
, (3.5.5)
то, например, математическое ожидание произведения 
запишется в виде
(3.5.6)
При постоянной плотности в правой части (3.5.6) отличны от нуля только первые два члена.
Большое количество корреляционных моментов, для которых, естественно, требуется подбирать на основе опыта замыкающие соотношения (при осреднении нелинейных членов 
, 
, 
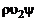и т.д.), побудило исследователей искать более удобные формы осреднения для описания течений с переменной плотностью. Наиболее удачная форма предложена Фавром. Метод Фавра предполагает осреднение всех параметров течения, кроме давления, по плотности. Например, средние значения проекций скорости определяются по формуле
(3.5.7)
Соответственно
. (3.5.8)
Для того чтобы отличить классический способ осреднения от осреднения по методу Фавра, в последнем случае средние значения будем обозначать 
, а пульсации – двумя штрихами вверху.
Применяя этот метод к слагаемым вида 
, получим
. (3.5.9)
Сравнивая соотношения (3.5.6) и (3.5.9), убеждаемся, что метод Фавра действительно позволяет существенно уменьшить число членов в правых частях этих соотношений для турбулентных течений с переменной плотностью. Если же плотность постоянна, то классический способ осреднения и осреднение по методу Фавра совпадают.
Применение метода Фавра к системе (3.5.1) – (3.5.4) позволяет получить уравнения для осредненных газодинамических параметров в форме, аналогичной уравнениям Рейнольдса для плоской струи несжимаемой жидкости:
· уравнение неразрывности
; (3.5.10)
· уравнение движения
; (3.5.11)
· уравнение энергии
(3.5.12)
· уравнение диффузии
(3.5.13)
По аналогии с ламинарным течением входящие в правые части уравнений (3.5.11) – (3.5.13) выражения 
, 
, 
можно рассматривать соответственно в качестве компонентов тензора добавочных турбулентных вязких напряжений и турбулентных составляющих векторов теплового потока и потоков диффузии вещества струи. Продолжая и далее аналогию с ламинарным течением, можно ввести коэффициенты турбулентной вязкости 
, турбулентной теплопроводности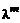 
, турбулентной диффузии 
:
, (3.5.14)
, (3.5.15)
, (3.5.16)
и турбулентные числа Прандтля 
и Шмидта 
, 
. (3.5.17)
Система уравнений для средних значений газодинамических параметров замыкается введением дополнительных полуэмпирических гипотез, постулирующих уравнения связи характеристик турбулентного переноса с осредненными параметрами течения.
В некоторых работах используется упрощенная схема получения замкнутых систем дифференциальных уравнений для осредненного турбулентного движения: уравнения для математических ожиданий газодинамических параметров записываются формально в таком же виде, как и для ламинарного течения, а турбулентные аналоги коэффициентов вязкости, теплопроводности и диффузии определяются по эмпирическим зависимостям.
