Задача определения вероятностных характеристик газодинамических параметровпри турбулентном смешении даже для простейших типов течения достаточно сложна. Для того чтобы понять суть возникающих проблем, предельно упростим постановку задачи. Будем считать газ несжимаемым 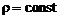 , массовые силы пренебрежимо малыми, а коэффициент динамической вязкости
, массовые силы пренебрежимо малыми, а коэффициент динамической вязкости  постоянным по всему полю течения. Тогда дифференциальные уравнения движения – уравнения Навье – Стокса – в прямоугольной декартовой системе координат записываются в виде (см. формулы (2.2.18), (2.2.19), (2.3.22)
постоянным по всему полю течения. Тогда дифференциальные уравнения движения – уравнения Навье – Стокса – в прямоугольной декартовой системе координат записываются в виде (см. формулы (2.2.18), (2.2.19), (2.3.22)
 (2.6.1)
(2.6.1)
Система (2.6.1) замыкается с помощью уравнения неразрывности
 . (2.6.2)
. (2.6.2)
Итак, имеем четыре уравнения (уравнение движения в проекциях на три оси декартовой системы координат (2.6.1) и уравнение неразрывности) для определения четырех неизвестных: трех проекций скорости на оси координат и давления. Решая систему уравнений в частных производных (2.6.1), (2.6.2) при соответствующих начальных и граничных условиях, получим искомые функции  и
и  . Казалось бы, имея мощную вычислительную технику, мы без особого труда можем во всех случаях решить уравнения (2.6.1), (2.6.2) численными методами, например методом конечных разностей. Однако в действительности все намного сложнее.
. Казалось бы, имея мощную вычислительную технику, мы без особого труда можем во всех случаях решить уравнения (2.6.1), (2.6.2) численными методами, например методом конечных разностей. Однако в действительности все намного сложнее.
Опыт показывает, что течение, описываемое уравнениями Навье-Стокса, при превышении  (
(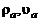 и
и  для изобарического участка струи – соответственно плотность, скорость и диаметр струи в начальном сечении) некоторых критических значений становится неустойчивым относительно малых возмущений. В результате потери устойчивости траектории жидких частиц приобретают запутанный, извилистый характер – движение из ламинарного становится турбулентным. Именно с турбулентными течениями мы чаще всего сталкиваемся на практике.
для изобарического участка струи – соответственно плотность, скорость и диаметр струи в начальном сечении) некоторых критических значений становится неустойчивым относительно малых возмущений. В результате потери устойчивости траектории жидких частиц приобретают запутанный, извилистый характер – движение из ламинарного становится турбулентным. Именно с турбулентными течениями мы чаще всего сталкиваемся на практике.
На первый взгляд представляется, что переход течения из ламинарного в турбулентное не очень сильно усложнит решение. В этом случае на начальные и граничные условия следует наложить, сообразуясь с условиями задачи, некоторые случайные колебания и затем статистически обработать полученные случайные величины  и р. Более подробный анализ показывает, что такой путь может быть реализован только при малых турбулентных числах Рейнольдса. Дело в том, что для адекватного описания течения конечноразностными уравнениями, заменяющими исходные дифференциальные уравнения в частных производных, приходится при турбулентном режиме дробить область течения на очень малые ячейки, размеры которых должны быть порядка самых малых размеров турбулентных вихрей. Сделанные оценки показали, что возможности даже самых мощных вычислительных машин пока недостаточны, чтобы обеспечить при этом требуемые объемы памяти и нужное быстродействие. С развитием вычислительной техники следует ожидать более широкого использования этих методов. Однако обсуждение этого вопроса выходит за рамки данного пособия.
и р. Более подробный анализ показывает, что такой путь может быть реализован только при малых турбулентных числах Рейнольдса. Дело в том, что для адекватного описания течения конечноразностными уравнениями, заменяющими исходные дифференциальные уравнения в частных производных, приходится при турбулентном режиме дробить область течения на очень малые ячейки, размеры которых должны быть порядка самых малых размеров турбулентных вихрей. Сделанные оценки показали, что возможности даже самых мощных вычислительных машин пока недостаточны, чтобы обеспечить при этом требуемые объемы памяти и нужное быстродействие. С развитием вычислительной техники следует ожидать более широкого использования этих методов. Однако обсуждение этого вопроса выходит за рамки данного пособия.
Итак, приходим к выводу, что мы не можем определить статистические характеристики газодинамических параметров в турбулентных течениях и, в частности, в турбулентных струях, решая уравнения для ламинарного течения с последующей статистической обработкой полученных результатов.
В 1881 г. О. Рейнольдс разделил газодинамические параметры на осредненные и пульсационные составляющие и, выполнив операцию осреднения над уравнениями Навье – Стокса, получил уравнения, называемые теперь уравнениями Рейнольдса, в которые характеристики пульсационного движения вошли в явном виде.
Выведем уравнения Рейнольдса. Для этого используем уравнение движения в так называем дивергентном виде (см. формулу (2.2.14)):
 . (2.6.3)
. (2.6.3)
Далее выделим средние значения (математические ожидания) газодинамических параметров и их комбинаций и отклонения от средних – пульсации

 (2.6.4)
(2.6.4)
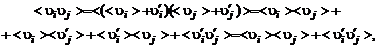 (2.6.5)
(2.6.5)
где знаком  обозначено среднее значение случайной величины, а штрихом вверху – ее пульсационная составляющая. Подставим (2.6.4) в (2.6.1) – (2.6.3). После осреднения преобразованных таким образом уравнений движения и неразрывности получим уравнения Рейнольдса:
обозначено среднее значение случайной величины, а штрихом вверху – ее пульсационная составляющая. Подставим (2.6.4) в (2.6.1) – (2.6.3). После осреднения преобразованных таким образом уравнений движения и неразрывности получим уравнения Рейнольдса:
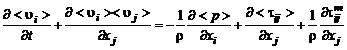 , (2.6.6)
, (2.6.6)
 , (2.6.7)
, (2.6.7)
 , (2.6.8)
, (2.6.8)
где через  обозначен симметричный тензор добавочных напряжений, вызванных турбулентным переносом:
обозначен симметричный тензор добавочных напряжений, вызванных турбулентным переносом:
 . (2.6.9)
. (2.6.9)
Шесть независимых компонентов тензора  представляют собой шесть новых неизвестных.
представляют собой шесть новых неизвестных.
Система уравнений (2.6.6) – (2.6.9) не замкнута, поэтому для ее решения необходимо, на основании опытных данных или каким-либо другим образом, получить замыкающие соотношения, связывающие искомые параметры между собой. С момента составления Рейнольдсом его уравнений появилось множество полуэмпирических теорий, существо которых состоит в замыкании этих уравнений с помощью дополнительных соотношений. Для некоторых простых типов движения, например для пограничного слоя, замыкающие соотношения для отдельных составляющих турбулентного трения удалось подобрать. Эти результаты будут рассмотрены далее в разд. 3. Однако даже для простейшего случая – несжимаемой жидкости или газа – такие замыкающие соотношения, пригодные для всех видов течения, не получены. Интересно в этом отношении высказывание известного гидромеханика Лайтхилла, охарактеризовавшего современное состояние науки о турбулентности, как «кладбище теорий, на котором каждая новая теория добавляет еще одну могилу».
Рассмотренный способ построения уравнений движения легко обобщается на уравнения энергии и диффузии. Но это приводит к появлению новых неизвестных вида  ,
,  и т.д.
и т.д.






