Определение математических ожиданий газодинамических параметров, а в ряде случаев и моментов более высокого порядка, в турбулентных течениях, в том числе и в турбулентных струях, с помощью уравнений Рейнольдса и замыкающих условий разной степени сложности сформировалось в теории турбулентных течений в самостоятельное направление. Появилось множество полуэмпирических теорий турбулентности, существо которых состоит в замыкании уравнений Рейнольдса с помощью дополнительных соотношений.
Рассмотрим некоторые из них для несжимаемой жидкости.
Итак, уравнения неразрывности и движения для осредненных параметров (см. формулы (2.6.6) – (2.6.9)) могут быть формально записаны в том же виде, что и для ламинарного движения, но будут содержать симметричный тензор добавочных турбулентных напряжений 
.
Первую попытку замкнуть систему уравнений движения, связав тензор 
с параметрами осредненного движения, сделал Буссинеск в 1877 г. еще до появления работы Рейнольдса. Согласно гипотезе Буссинеска, между тензором турбулентных напряжений и тензором осредненных скоростей деформации существует связь, аналогичная линейной связи между тензором вязких напряжений и тензором скоростей деформации ламинарного течения:
. (3.2.1)
В отличие от ламинарного течения, коэффициент турбулентной вязкости 
не является постоянной величиной, а определяется начальными и граничными условиями, характером движения и в общем случае представляет собой скалярную функцию координат пространства.
При развитом турбулентном течении, в достаточном удалении от стенок, напряжения молекулярной вязкости пренебрежимо малы по сравнению с турбулентными. Это позволяет опустить в (2.6.6) член 
. В результате получим уравнения Буссинеска:
, (3.2.2)
, (3.2.3)
. 
(3.2.4)
Однако формула (3.2.3), написанная по аналогии с ламинарным течением несжимаемой жидкости, не вполне корректна. Это связано с тем, что, в отличие от ламинарного течения, сумма нормальных компонентов турбулентных сил трения не равна нулю:
. (3.2.5)
Так как кинетическая энергия турбулентности в единице массы равна:
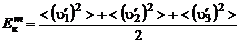, (3.2.6)
то
. (3.2.7)
Для устранения указанной некорректности А.Н. Колмогоров в 1942 г. предложил новый вариант гипотезы о связи между тензором турбулентных сил трения и тензором скоростей деформации осредненного поля:
, (3.2.8)
где 
Система уравнений (3.2.2), (3.2.8), (3.2.4) требует для своего замыкания дополнительных зависимостей, определяющих коэффициент турбулентной вязкости и кинетическую энергию турбулентности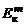 
. Наибольшей популярностью пользуется
модель, в которой замыкание достигается введением дифференциальных уравнений типа уравнений переноса для и 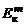( 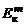– модель).
Модели типа 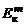– обладают высокой универсальностью, позволяя находить математические ожидания газодинамических параметров не только в турбулентных струях, но и в сложных пространственных течениях с большими градиентами давления. Однако эта универсальность достигается введением дополнительного набора опытных констант, зачастую меняющихся в зависимости от характера течения, и требует значительных затрат времени на проведение расчетов без увеличения точности получаемых результатов. Поэтому применение указанной модели для расчета турбулентных струй нецелесообразно.
Уравнения пограничного слоя. В 1904 г. Прандтль упростил уравнения Навье – Стокса применительно к задачам о течении в пограничном слое. Существо этих упрощений сводится к выделению узких зон, называемых пограничными слоями, в которых продольные градиенты газодинамических величин пренебрежимо малы по сравнению с поперечными.
Запишем, например, уравнения Буссинеска – Колмогорова для стационарной плоскопараллельной турбулентной струи несжимаемой жидкости или газа с учетом приближений пограничного слоя:
, (3.2.9)
, (3.2.10)
, (3.2.11)
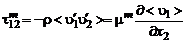, (3.2.12)
где 
– продольная координата, отсчитываемая от среза сопла по оси струи или параллельно ей;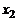 
– поперечная координата.
К настоящему времени известно много теорий струйной или так называемой свободной турбулентности, основанных на замыкании системы уравнений пограничного слоя. Остановимся на трех: старой теории Прандтля, теории Тейлора и новой теории Прандтля, как получивших наибольшее признание и широко используемых. Для удобства и наглядности суть рассматриваемых теорий поясним на примере простейшего типа струйного тече-ния – течения в стационарной плоскопараллельной изобарической струе несжимаемой жидкости.
Старая теория свободной турбулентности Прандтля. Займемся анализом формулы (3.2.12) для турбулентного трения. Введем среднеквадратические значения пульсаций скорости в продольном и поперечном направлениях:
, 
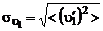. (3.2.13)
Корреляционная функция 
может быть представлена в нормированном виде:
, (3.2.14)
где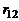 
– коэффициент корреляции, который по определению меняется в пределах 
. Прандтль предложил считать коэффициент корреляции 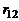равным 
. Знак «минус» соответствует положительному градиенту продольной скорости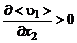 
, а «плюс» – отрицательному 
. Поясним это предположение. Пусть 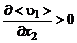. Тогда жидкие частицы, перемещаясь в положительном направлении оси , 
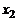, вызывают отрицательные пульсации продольной составляющей скорости 
и, наоборот, если 
, то 
. Такое же рассуждение для приводит к одинаковым знакам при 
и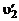 
.
В свою очередь величина 
предполагается пропорциональной модулю градиента осредненной продольной скорости в поперечном направлении:
. (3.2.15)
Названный Прандтлем "путь смешения" 
в рассматриваемой модели линейно зависит от продольной координаты:
, (3.2.16)
где 
– единственная эмпирическая постоянная теории свободной турбулентности Прандтля.
Подставляя (3.2.16), (3.2.15), (3.2.14) в (3.2.12) и предполагая равенство 
, получим следующую известную формулу турбулентного трения Прандтля:
. (3.2.17)
Здесь знак «плюс» берется при 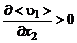. Формулу (3.2.17) можно записать в ином виде:
. (3.2.18)
Используя выражение для турбулентного трения (3.2.18) и подставляя его в (3.2.9) при 
, получим замкнутую систему двух уравнений, описывающую поле скоростей в плоской струе несжимаемой жидкости:
(3.2.19)
Толмин применил старую теорию свободной турбулентности Прандтля к решению трех задач о распространении свободных затопленных струй несжимаемой жидкости: о пограничном слое беспредельной плоской струи; о плоской струе, вытекающей из очень узкого отверстия; об осесимметричной струе, вытекающей из очень узкого отверстия. Во всех случаях Толмину удалось подбором одной опытной константы 
добиться хорошего согласия экспериментальных и теоретических результатов.
Теория Прандтля может быть обобщена на решение тепловой и диффузионных задач.
Для отыскания закона распределения температур в плоской струе воспользуемся уравнением энергии (2.4.12) с учетом следующих допущений (помимо тех, которые уже приняты: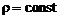 
, , движение установившееся, струя плоская):
· скорости малы, что позволяет пренебречь кинетической энергией в выражении для полного теплосодержания:
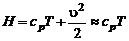; (3.2.20)
· массовые силы пренебрежимо малы: 
;
· молекулярной теплопроводностью и переходом работы вязких сил в тепло пренебрегаем вследствие их малости по сравнению с турбулентным переносом тепла;
· объемное выделение тепла равно нулю: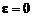 
.
Выполнив операцию осреднения газодинамических параметров и их комбинаций, получим уравнение энергии для плоского пограничного слоя в виде
, (3.2.21)
где турбулентный тепловой поток в поперечном направлении равен:
. (3.2.22)
Здесь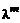 
– коэффициент турбулентной теплопроводности.
Применим подход Прандтля при подборе замыкающего соотношения для корреляционной функции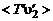 
. Запишем ее в виде
, (3.2.23)
где знак «минус» соответствует положительному поперечному градиенту температуры 
; 
– среднеквадратическое значение пульсации температуры.
Полагая, что
, (3.2.24)
, (3.2.25)
получим выражение для корреляционной функции :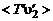
. (3.2.26)
Подставляя (3.2.22) и (3.2.26) в (3.2.21) и учитывая уравнение неразрывности (3.2.11), приходим к уравнению энергии для плоской изобарической турбулентной струи:
(3.2.27)
В формулу (3.2.27) приходятся вводить уже две опытные константы: и 
, так как, по экспериментальным данным, тепловой турбулентный слой толще динамического. Соответственно турбулентное число Прандтля 
, определяемое как отношение:
, (3.2.28)
меньше единицы (опытное значение 
).
Применив аналогичные рассуждения к уравнению диффузии пассивной примеси (2.5.10), получим уравнение диффузии для плоской турбулентной струи:
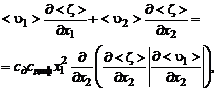(3.2.29)
где 
– массовая концентрация пассивной примеси.
Сопоставление полученных из опыта профилей нормированных избыточных температур 
и массовой концентрации пассивной примеси показало их идентичность, что позволяет считать
, (3.2.30)
, (3.2.31)
где 
– температура на срезе сопла, 
– температура окружающей среды.
Таким образом, решение динамической, тепловой и диффузионных задач в рамках старой теории турбулентности Прандтля требует введения двух опытных констант: и .
Теория свободной турбулентности Тейлора. Физическая модель турбулентности Тейлора исходит из предположения, что турбулентное трение вызывается переносом вихрей, а не количества движения, как в старой теории свободной турбулентности Прандтля. В результате Тейлор получил уравнения движения, энергии и диффузии эквивалентные соответствующим уравнениям старой теории Прандтля при условии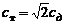 
. Турбулентное число Прандтля в теории Тейлора равно 
, что хорошо согласуется с экспериментальными данными.
Тем самым Тейлор построил замкнутую систему уравнений для определения осредненных газодинамических параметров в струе несжимаемой жидкости, используя лишь одну опытную константу .
Новая теория свободной турбулентности Прандтля. Новая теория турбулентности Прандтля (1942), базируется на допущении о постоянстве коэффициента турбулентной вязкости по сечению струи:
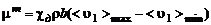, (3.2.32)
где 
– ширина зоны смешения, определяемая по эмпирическим формулам, 
– опытная константа.
Уравнение (3.2.32) с точки зрения точности описания течения в турбулентных струях не имеет преимуществ перед соотношением для коэффициента турбулентной вязкости:
, (3.2.33)
используемого в старой теории турбулентности Прандтля, но не приводит к противоречащему действительности требованию обращения в нуль в точках слоя смешения, где 
.
