Перейдем к определению математических ожиданий начальных моментов газодинамических комплексов  в произвольной точке
в произвольной точке  на изобарическом участке струи.
на изобарическом участке струи.
Имея в виду унификацию расчетных соотношений и согласование их с решениями, получаемыми по модели Рейхардта, введем новые переменные
 . (4.4.1)
. (4.4.1)
Кроме того, нормируем комплексы  , поделив их на максимальные по модулю величины
, поделив их на максимальные по модулю величины  в сечении а – а:
в сечении а – а:  . В результате значения
. В результате значения  будут меняться в интервале
будут меняться в интервале  . С учетом этих преобразований уравнения (4.1.7) – (4.1.9) сведутся к следующим выражениям для математических ожиданий
. С учетом этих преобразований уравнения (4.1.7) – (4.1.9) сведутся к следующим выражениям для математических ожиданий  и
и  в точке
в точке  :
:
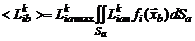 , (4.4.2)
, (4.4.2)
 , (4.4.3)
, (4.4.3)
где k =1 при определении  и k =2 при определении
и k =2 при определении  .
.
На больших удалениях от среза одиночного сопла или выходных сечений блока сопл ( ) из-под знака интеграла в формуле (4.4.2) можно вынести функцию
) из-под знака интеграла в формуле (4.4.2) можно вынести функцию  . В результате для этого предельного случая найдем распределения
. В результате для этого предельного случая найдем распределения  по сечению b – b струи, характерные для точечного источника:
по сечению b – b струи, характерные для точечного источника:
 , (4.4.4)
, (4.4.4)
 , (4.4.5)
, (4.4.5)
где  – математическое ожидание комплекса
– математическое ожидание комплекса  в сечении b – b на оси.
в сечении b – b на оси.
Соотношения (4.4.2) и (4.4.3) легко обобщаются на блочные струи. Если отдельные струи блока взаимодействуют только на изобарическом участке, то выполняется принцип сложения решений:
 , (4.4.6)
, (4.4.6)
где  – значение
– значение  в заданной точке от воздействия всех струй блока;
в заданной точке от воздействия всех струй блока;  – значение
– значение  в заданной точке от воздействия только j -й струи; N – число струй в блоке.
в заданной точке от воздействия только j -й струи; N – число струй в блоке.
Основные соотношения для круглых струй. Теперь займемся вычислением интегралов (4.4.2), (4.4.3) для круглых струй. Введем цилиндрическую систему координат (рис. 4.8):
 ;
;  ;
;  . (4.4.7)
. (4.4.7)

Рис. 4.8
Поместим начальное сечение а – а в плоскость 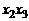 , а ось струи совместим с координатной осью
, а ось струи совместим с координатной осью  . Тогда, подставляя (4.4.7) в (4.4.2), после несложных преобразований получим
. Тогда, подставляя (4.4.7) в (4.4.2), после несложных преобразований получим
 (4.4.8)
(4.4.8)
где  – диаметр струи в начальном сечении. Будем отсчитывать полярный угол
– диаметр струи в начальном сечении. Будем отсчитывать полярный угол  от плоскости, проходящей через точку
от плоскости, проходящей через точку  , и учтем известную зависимость
, и учтем известную зависимость
 , (4.4.9)
, (4.4.9)
где  – функция Бесселя первого рода нулевого порядка от мнимого аргумента. Так как
– функция Бесселя первого рода нулевого порядка от мнимого аргумента. Так как  – четная функция от
– четная функция от  , то
, то
 , (4.4.10)
, (4.4.10)
 . (4.4.11)
. (4.4.11)
Если величины  распределены равномерно по начальному сечению, т.е.
распределены равномерно по начальному сечению, т.е.  =1,
=1,  , и линейные размеры отнесены к
, и линейные размеры отнесены к  , то (4.4.11) можно записать в виде
, то (4.4.11) можно записать в виде
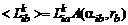 , (4.4.12)
, (4.4.12)
 . (4.4.13)
. (4.4.13)
На оси струи интеграл  выражается через элементарные функции:
выражается через элементарные функции:
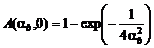 . (4.4.14)
. (4.4.14)
Приведем интеграл в правой части (4.4.11) к виду, удобному для вычисления. Преобразуем подынтегральное выражение:

 (4.4.15)
(4.4.15)
и введем для сокращения записи новые переменные:
 ,
,  . (4.4.16)
. (4.4.16)
Тогда
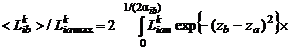
 (4.4.17)
(4.4.17)
Функция Бесселя нулевого порядка от мнимого аргумента находится с помощью асимптотических разложений:
при 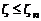
 , (4.4.18)
, (4.4.18)
при 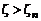
 . (4.4.19)
. (4.4.19)
Соответственно функция  с учетом (4.4.18), (4.4.19) представляется в виде:
с учетом (4.4.18), (4.4.19) представляется в виде:
при 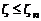
 , (4.4.20)
, (4.4.20)
при 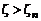
 . (4.4.21)
. (4.4.21)
Исследование соотношений (4.4.20), (4.4.21) показало, что для обеспечения относительной погрешности вычисления функции  не более
не более  при
при  следует в разложениях
следует в разложениях  в ряды при
в ряды при 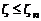 брать не менее восьми, а при
брать не менее восьми, а при 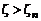 – не менее шести членов.
– не менее шести членов.
С учетом сделанных преобразований (4.4.17) запишется в форме
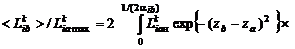
 (4.4.22)
(4.4.22)
Естественно поставить вопрос: зачем нам потребовалось приводить уравнение (4.4.11) к виду (4.4.22)? Чтобы ответить на него, рассмотрим поведение подынтегральных функций в (4.4.11), (4.4.22) при  . Легко заметить, что в (4.4.11) возникает неопределенность вида
. Легко заметить, что в (4.4.11) возникает неопределенность вида  . К бесконечности стремится функция Бесселя нулевого порядка от мнимого аргумента при уменьшении
. К бесконечности стремится функция Бесселя нулевого порядка от мнимого аргумента при уменьшении  . Практически это означает, что, используя (4.4.11), следует предусмотреть ограничения на возможные значения
. Практически это означает, что, используя (4.4.11), следует предусмотреть ограничения на возможные значения  . В противном случае произойдет выход порядка сомножителей за допустимые пределы. В формуле (4.4.22) эта неопределенность устранена. Действительно, функция
. В противном случае произойдет выход порядка сомножителей за допустимые пределы. В формуле (4.4.22) эта неопределенность устранена. Действительно, функция  ограничена, и при любых значениях
ограничена, и при любых значениях  ее значения лежат в пределах
ее значения лежат в пределах 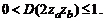
При вычислении интеграла в (4.4.22) следует учитывать еще одну особенность, возникающую при расчете  в сечениях, близких к начальному. Если величины
в сечениях, близких к начальному. Если величины  и, соответственно,
и, соответственно,  малы, то резко увеличивается значение верхнего предела
малы, то резко увеличивается значение верхнего предела  в интеграле (4.4.22). Предполагается, что допустимая ошибка одинакова для всех точек, и, следовательно, шаг по
в интеграле (4.4.22). Предполагается, что допустимая ошибка одинакова для всех точек, и, следовательно, шаг по  постоянен.
постоянен.
Заметим, что в исходном интеграле (4.4.11) с постоянными верхним и нижним пределами также будет наблюдаться рост объема вычислений при нахождении этого интеграла с требуемой точностью, когда  и
и 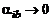 , из-за необходимости уменьшения шага по
, из-за необходимости уменьшения шага по 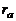 .
.
Объем вычислений при нахождении интеграла в (4.4.22) в случае малых величин  можно существенно сократить, если учесть следующее обстоятельство. Функция
можно существенно сократить, если учесть следующее обстоятельство. Функция  быстро убывает с ростом величины абсолютного значения разности
быстро убывает с ростом величины абсолютного значения разности  , а функция
, а функция  ограничена. В результате на большей части промежутка интегрирования подынтегральная функция с достаточной степенью точности может быть принята равной нулю. Целесообразно поэтому из всего промежутка интегрирования от 0 до
ограничена. В результате на большей части промежутка интегрирования подынтегральная функция с достаточной степенью точности может быть принята равной нулю. Целесообразно поэтому из всего промежутка интегрирования от 0 до  вырезать отрезок
вырезать отрезок  , где
, где  определяется допускаемой относительной погрешностью. Оценим величину
определяется допускаемой относительной погрешностью. Оценим величину  . Пусть
. Пусть  ,
, 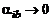 ,
, 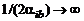 . Тогда для всех точек сечения, удовлетворяющих условию
. Тогда для всех точек сечения, удовлетворяющих условию  , при равномерном распределении параметров в начальном сечении изобарического участка
, при равномерном распределении параметров в начальном сечении изобарического участка  отношение
отношение  . Примем
. Примем 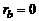 , что даст нам максимум в рассматриваемой оценке, ибо
, что даст нам максимум в рассматриваемой оценке, ибо 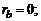

 , и заменим верхний предел интегрирования
, и заменим верхний предел интегрирования  в (4.4.22) на
в (4.4.22) на  . При этом относительная погрешность вычисления интеграла, вызванная сужением интервала интегрирования, определится зависимостью
. При этом относительная погрешность вычисления интеграла, вызванная сужением интервала интегрирования, определится зависимостью
 . (4.4.23)
. (4.4.23)
Если значение  принять равным 5, то при вычислении интеграла в (4.4.22) относительная погрешность
принять равным 5, то при вычислении интеграла в (4.4.22) относительная погрешность  не превысит значения
не превысит значения  .
.
Общие сведения о связи обобщенных продольных координат  с физической
с физической  . Соотношения (4.4.2) и (4.4.22) дляопределения начальных моментов
. Соотношения (4.4.2) и (4.4.22) дляопределения начальных моментов 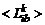 содержат неизвестные величины
содержат неизвестные величины  , которые характеризуют отклонения квазичастиц от прямолинейных траекторий при их случайном блуждании. Эти величины при фиксированных параметрах на срезе сопла и в окружающей среде имеют размерность длины и зависят от продольной физической координаты
, которые характеризуют отклонения квазичастиц от прямолинейных траекторий при их случайном блуждании. Эти величины при фиксированных параметрах на срезе сопла и в окружающей среде имеют размерность длины и зависят от продольной физической координаты  . Поэтому они были названы обобщенными продольными координатами точки
. Поэтому они были названы обобщенными продольными координатами точки  . Связь обобщенных
. Связь обобщенных  и физической
и физической  продольных координат устанавливается из опыта.
продольных координат устанавливается из опыта.
Приведем сводку формул для определения в круглых струях обобщенных координат  по заданным величинам
по заданным величинам  . Эти формулы получены в результате обработки обширного материала по экспериментальному изучению турбулентных течений и охватывают большинство встречающихся на практике типов струй.
. Эти формулы получены в результате обработки обширного материала по экспериментальному изучению турбулентных течений и охватывают большинство встречающихся на практике типов струй.
Обобщенные координаты  связаны друг с другом простыми зависимостями
связаны друг с другом простыми зависимостями
 , (4.4.24)
, (4.4.24)
которые достаточно точно выполняются при всех сочетаниях параметров на срезе сопла и в окружающей среде. Следовательно, нам нужно установить связь с физической продольной координатой  только одной из переменных
только одной из переменных  , например
, например  .
.
Анализ показал, что на ход кривых  влияют следующие факторы: среднемассовое число Маха
влияют следующие факторы: среднемассовое число Маха  , нерасчетность n, отношение плотностей
, нерасчетность n, отношение плотностей  и скорость спутного потока.
и скорость спутного потока.
Опытные зависимости  для затопленных
для затопленных
дозвуковых струй. В дозвуковых затопленных струях число значимых факторов сводится к двум: числу Маха в начальном сечении изобарического участка и отношению плотностей струи и окружающей среды  . Рассмотрим воздействие каждого из этих факторов отдельно, а затем их совместное воздействие на зависимость
. Рассмотрим воздействие каждого из этих факторов отдельно, а затем их совместное воздействие на зависимость  .
.
Пусть плотность в струе равна плотности в окружающей среде  . Так как струя истекает в затопленное пространство при скоростях, меньших скорости звука, то начальное сечение изобарического участка совпадает со срезом сопла, а значения
. Так как струя истекает в затопленное пространство при скоростях, меньших скорости звука, то начальное сечение изобарического участка совпадает со срезом сопла, а значения  и
и 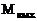 равны.
равны.
При  связь обобщенной продольной координаты
связь обобщенной продольной координаты  с физической
с физической  дается формулой
дается формулой
 , (4.4.25)
, (4.4.25)
где постоянная 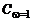 принимается равной:
принимается равной:
 , (4.4.26)
, (4.4.26)
 (4.4.27)
(4.4.27)
 . (4.4.28)
. (4.4.28)
Приведем теперь формулы, учитывающие влияние различий в плотностях струи и окружающей среды на зависимость  . Введем параметр
. Введем параметр  :
:
 , (4.4.29)
, (4.4.29)
который характеризует отношение плотности окружающей среды к средней по сечению плотности струи. Для круглой струи
 . (4.4.30)
. (4.4.30)
Экспериментальные исследования показали, что с ростом значения  производная
производная 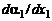 медленно увеличивается.
медленно увеличивается.
Если параметр  меняется в пределах
меняется в пределах  , то для определения зависимости
, то для определения зависимости  может быть сохранена линейная модель
может быть сохранена линейная модель
 , (4.4.31)
, (4.4.31)
где постоянная  ,
,  – опытная зависимость,
– опытная зависимость,
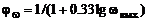 , (4.4.32)
, (4.4.32)
 – значение параметра
– значение параметра  на срезе сопла. Формула (4.4.32) записана для таких типов струй, в которых плотность изменяется только из-за перемешивания вещества струи с окружающей средой.
на срезе сопла. Формула (4.4.32) записана для таких типов струй, в которых плотность изменяется только из-за перемешивания вещества струи с окружающей средой.
В струях с диффузионным факелом горения процесс перемешивания сопровождается выделением химической энергии при догорании продуктов неполного окисления топлива в атмосфере. Это вызывает повышение температуры в зоне факела и увеличение  , так как увеличение температуры при постоянном давлении эквивалентно уменьшению плотности ρ. Зависимости (4.4.31), (4.4.32) остаются справедливыми и для струй с факелом, но в (4.4.32) вместо
, так как увеличение температуры при постоянном давлении эквивалентно уменьшению плотности ρ. Зависимости (4.4.31), (4.4.32) остаются справедливыми и для струй с факелом, но в (4.4.32) вместо  следует подставить среднее по длине факела значение
следует подставить среднее по длине факела значение  .
.
При совместном воздействии обоих факторов – числа Маха на срезе сопла и параметра ω – зависимость  для дозвуковой затопленной струи остается линейной:
для дозвуковой затопленной струи остается линейной:
 , (4.4.33)
, (4.4.33)
где корректирующие сомножители находятся соответственно по (4.4.27), (4.4.32).
Если значения ω в струе выходят за пределы интервала  , то производная
, то производная 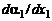 будет заметно меняться по длине струи. Такая ситуация обычна, например, для струй плазмы. Использование линейной зависимости (4.4.33) в этом случае приведет к большим ошибкам. Здесь уже требуется интегрировать уравнение
будет заметно меняться по длине струи. Такая ситуация обычна, например, для струй плазмы. Использование линейной зависимости (4.4.33) в этом случае приведет к большим ошибкам. Здесь уже требуется интегрировать уравнение
 , (4.4.34)
, (4.4.34)
которое аппроксимирует экспериментальные результаты при изменении параметра ω в диапазоне  .
.
Опытные зависимости  для затопленных сверхзвуковых струй. При переходе от дозвуковых скоростей к сверхзвуковым выделим в затопленной струе две части: сверхзвуковую и дозвуковую. Границей между ними будет сечение, начиная с которого поток становится дозвуковым по всему полю струи. Пусть продольная координата этого сечения
для затопленных сверхзвуковых струй. При переходе от дозвуковых скоростей к сверхзвуковым выделим в затопленной струе две части: сверхзвуковую и дозвуковую. Границей между ними будет сечение, начиная с которого поток становится дозвуковым по всему полю струи. Пусть продольная координата этого сечения  .
.
Расчет газодинамических параметров в сечениях струй с координатой  показал, что в этих сечениях среднемассовое число Маха
показал, что в этих сечениях среднемассовое число Маха  близко к 0,5, а число Маха на оси струи
близко к 0,5, а число Маха на оси струи  равно единице. За указанными сечениями вниз по потоку
равно единице. За указанными сечениями вниз по потоку
 , (4.4.35)
, (4.4.35)
где  ;
;  ; значение
; значение  соответствует продольной координате конца сверхзвуковой части струи:
соответствует продольной координате конца сверхзвуковой части струи:  . Величина коэффициента пропорциональности С в (4.4.35) находится в том же диапазоне, что и для рассмотренных ранее затопленных струй малой скорости
. Величина коэффициента пропорциональности С в (4.4.35) находится в том же диапазоне, что и для рассмотренных ранее затопленных струй малой скорости  .
.
Длина сверхзвуковой части струи  определяется до значений
определяется до значений  по формуле
по формуле
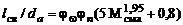 , (4.4.36)
, (4.4.36)
где  и
и  соответственно значения диаметра начального сечения изобарического участка и среднемассового числа Маха в нем.
соответственно значения диаметра начального сечения изобарического участка и среднемассового числа Маха в нем.
Коэффициент 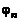 учитывает влияние нерасчетности n:
учитывает влияние нерасчетности n:

 ; (4.4.37)
; (4.4.37)

 .
.
Коэффициент  связан с изменением параметра ω по длине турбулентной струи. Определяется он точно так же, как и для дозвуковых струй. Для струй ракетных двигателей, например, коэффициент
связан с изменением параметра ω по длине турбулентной струи. Определяется он точно так же, как и для дозвуковых струй. Для струй ракетных двигателей, например, коэффициент  примерно одинаков и равен:
примерно одинаков и равен:  . Для неизотермических струй без физико-химических превращений
. Для неизотермических струй без физико-химических превращений  может быть вычислен по формуле
может быть вычислен по формуле
 . (4.4.38)
. (4.4.38)
Поставим теперь в соответствие длине сверхзвуковой части струи  обобщенную продольную координату
обобщенную продольную координату 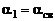 .
.
Значение  определяется по формуле
определяется по формуле
 , (4.4.39)
, (4.4.39)
где  – диаметр выходного сечения сопла.
– диаметр выходного сечения сопла.
Приближенно полагаем, ввиду небольшого диапазона возможных изменений показателя адиабаты  , что
, что
 . (4.4.40)
. (4.4.40)
Итак, мы имеем два опорных сечения: срез сопла  ,
, 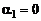 и сечение, отделяющее сверхзвуковую и дозвуковую области струи,
и сечение, отделяющее сверхзвуковую и дозвуковую области струи,  ,
, 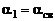 .
.
Для дозвуковой области струи зависимость  известна – это соотношение (4.4.35). Для сверхзвуковой области обработка опытных данных в широком диапазоне изменения среднемассового числа Маха в начальном сечении изобарического участка
известна – это соотношение (4.4.35). Для сверхзвуковой области обработка опытных данных в широком диапазоне изменения среднемассового числа Маха в начальном сечении изобарического участка  приводит к формуле
приводит к формуле
 (4.4.41)
(4.4.41)
где  .
.
Влияние спутного потока на зависимость  . Введем параметр спутности
. Введем параметр спутности
 , (4.4.42)
, (4.4.42)
где  – средняя по начальному сечению изобарического участка скорость струи. При дозвуковых скоростях истечения
– средняя по начальному сечению изобарического участка скорость струи. При дозвуковых скоростях истечения  , так как в этом случае выходное сечение сопла и начальное сечение изобарического участка совпадают.
, так как в этом случае выходное сечение сопла и начальное сечение изобарического участка совпадают.
Влияние параметра спутности  сводится просто к изменению масштаба зависимости
сводится просто к изменению масштаба зависимости  , полученной для затопленной струи
, полученной для затопленной струи
 , (4.4.43)
, (4.4.43)
где 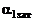 – обобщенная продольная координата
– обобщенная продольная координата  для затопленной струи,
для затопленной струи,  – коэффициент, учитывающий спутный поток.
– коэффициент, учитывающий спутный поток.
Кусочно-параболическая аппроксимация зависимости  , обобщающая результаты большого числа экспериментальных исследований при
, обобщающая результаты большого числа экспериментальных исследований при 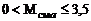 , имеет вид
, имеет вид

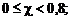


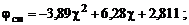
 (4.4.44)
(4.4.44)



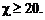
Зависимости  для блочных струй. Для получения опытных зависимостей
для блочных струй. Для получения опытных зависимостей  разделим блочные затопленные струи на две группы. К первой группе отнесем те блочные струи, в которых в зоне взаимодействия одиночных струй, входящих в блок, скорости дозвуковые. Тогда в выбранной точке турбулентной блочной струи комплексы
разделим блочные затопленные струи на две группы. К первой группе отнесем те блочные струи, в которых в зоне взаимодействия одиночных струй, входящих в блок, скорости дозвуковые. Тогда в выбранной точке турбулентной блочной струи комплексы  определяются в соответствии с принципом суперпозиции (см. (4.4.6)), а зависимости
определяются в соответствии с принципом суперпозиции (см. (4.4.6)), а зависимости  , используемые при нахождении значений комплекса
, используемые при нахождении значений комплекса  от воздействия отдельной j -й струи, входящей в блок, считаются такими же, как для соответствующих одиночных струй.
от воздействия отдельной j -й струи, входящей в блок, считаются такими же, как для соответствующих одиночных струй.
Ко второй группе отнесем затопленные блочные струи, в которых взаимное влияние отдельных струй, входящих в блок, обнаруживается уже в пределах области сверхзвуковых скоростей. Схема расчета зависимостей  для блочной струи в этом случае строится следующим образом. До соприкосновения струй блока параметры в них, в том числе зависимости
для блочной струи в этом случае строится следующим образом. До соприкосновения струй блока параметры в них, в том числе зависимости  , рассчитываются для каждой струи отдельно. Сечение, начиная с которого наблюдается взаимное наложение пограничных слоев струй блока и формирование одной струи сложной формы, принимается за начальное сечение а–а изобарического участка одиночной струи. Далее расчет проводится так же, как для одиночной струи.
, рассчитываются для каждой струи отдельно. Сечение, начиная с которого наблюдается взаимное наложение пограничных слоев струй блока и формирование одной струи сложной формы, принимается за начальное сечение а–а изобарического участка одиночной струи. Далее расчет проводится так же, как для одиночной струи.
В заключение остановимся еще на одной особенности расчета зависимостей  для блочных струй. Речь идет о явлении «слипания» струй блока. При большой кривизне осей отдельных струй продольную физическую координату
для блочных струй. Речь идет о явлении «слипания» струй блока. При большой кривизне осей отдельных струй продольную физическую координату  следует отсчитывать вдоль фактических осей струй с учетом их сближения в составной струе.
следует отсчитывать вдоль фактических осей струй с учетом их сближения в составной струе.
Анализ опытных данных показал, что основным фактором, определяющим сближение отдельных струй, истекающих из блока сопл, является геометрия блока, а начальный подогрев, физико-химические превращения и состав газа на срезах сопл слабо влияют на этот процесс. Указанное свойство блочных струй позволяет при опытном определении отклонений осей струй, входящих в блок, проводить моделирование на «холодных» струях.
4.5. Определение газодинамических параметров по заданным
величинам комплексов 
При определении статистических характеристик газодинамических параметров (математических ожиданий и среднеквадратических отклонений) нам неоднократно потребуется находить газодинамические параметры по известным величинам комплексов  .
.
Итак, пусть известны комплексы  , параметры окружающей среды и таблично заданные функции
, параметры окружающей среды и таблично заданные функции 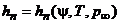 ,
,  ,
,  . Всю систему уравнений, определяющую значения газодинамических параметров на изобарическом участке
. Всю систему уравнений, определяющую значения газодинамических параметров на изобарическом участке  , разобьем на две части. К первой отнесем те уравнения, которые решаются совместно. Это система из семи уравнений:
, разобьем на две части. К первой отнесем те уравнения, которые решаются совместно. Это система из семи уравнений:




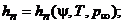 (4.5.1)
(4.5.1)

 ,
,
определяющая семь неизвестных: 
Заметим, что система (4.5.1) имеет один и тот же вид, как для струй с «замороженным» составом, так и для струй с равновесными физико-химическими превращениями. Различие будет лишь в таблицах  ,
,  ,
,  . Более того, одни и те же таблицы могут быть использованы для расчета и равновесного, и “замороженного” истечения. В последнем случае в таблицах следует оставить только те значения
. Более того, одни и те же таблицы могут быть использованы для расчета и равновесного, и “замороженного” истечения. В последнем случае в таблицах следует оставить только те значения  , R и
, R и  , которые соответствуют величинам
, которые соответствуют величинам  и
и  . Вследствие линейности зависимостей
. Вследствие линейности зависимостей  и
и  от параметра
от параметра  при механическом смешении без химических реакций из построенных таким образом таблиц будем иметь термодинамические характеристики для «замороженного» истечения. Так как показатель адиабаты меняется незначительно, то и его зависимость от
при механическом смешении без химических реакций из построенных таким образом таблиц будем иметь термодинамические характеристики для «замороженного» истечения. Так как показатель адиабаты меняется незначительно, то и его зависимость от  для «замороженного» состава близка к линейной. Для расчета параметров при равновесном истечении используются полные таблицы термодинамических характеристик.
для «замороженного» состава близка к линейной. Для расчета параметров при равновесном истечении используются полные таблицы термодинамических характеристик.
Система (4.5.1) решается следующим образом. Разделив первое и второе ее уравнения на третье, получим цепочку соотношений, последовательно определяющих газодинамические параметры в зависимости от переменной  , параметров окружающей среды и комплексов
, параметров окружающей среды и комплексов  :
:



 (4.5.2)
(4.5.2)


При определении значения  используем метод половинного деления для нахождения корня на отрезке
используем метод половинного деления для нахождения корня на отрезке  . Замыкающим уравнением, позволяющим определить
. Замыкающим уравнением, позволяющим определить  , может быть, например, первое уравнение системы (4.5.1).
, может быть, например, первое уравнение системы (4.5.1).
В соответствии с методом половинного деления в первом приближении нижнюю и верхнюю границы диапазонов изменения  принимаем равными:
принимаем равными:  ,
, 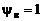 , где индексом «н» будем обозначать газодинамические параметры на нижней, а индексом «в» – на верхней границах. Делим промежуток
, где индексом «н» будем обозначать газодинамические параметры на нижней, а индексом «в» – на верхней границах. Делим промежуток  пополам, определяем среднюю точку
пополам, определяем среднюю точку  и находим значения газодинамических параметров при
и находим значения газодинамических параметров при  по системе (4.5.2). Если
по системе (4.5.2). Если
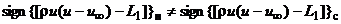 , (4.5.3)
, (4.5.3)
где  и
и  – значения выражения
– значения выражения  соответственно при
соответственно при  и
и  , то значение
, то значение  , обеспечивающее выполнение замыкающего условия
, обеспечивающее выполнение замыкающего условия 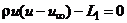 , будет в промежутке от
, будет в промежутке от  до
до 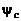 . Тогда принимаем
. Тогда принимаем 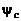 за новую верхнюю границу
за новую верхнюю границу  . В противоположном случае
. В противоположном случае  . Сузив таким образом диапазон, в котором находится искомое значение
. Сузив таким образом диапазон, в котором находится искомое значение  , снова делим этот диапазон пополам и повторяем все вычисления. Процесс сближения продолжается до тех пор, пока разность
, снова делим этот диапазон пополам и повторяем все вычисления. Процесс сближения продолжается до тех пор, пока разность  не станет меньше допускаемой ошибки вычисления
не станет меньше допускаемой ошибки вычисления  . В результате решения (4.5.1) изложенным методом получим следующие параметры:
. В результате решения (4.5.1) изложенным методом получим следующие параметры: 
Ко второй части отнесем вспомогательные уравнения, выражающие остальные газодинамические параметры и их комбинации через уже вычисленные. Это формулы для определения показателя адиабаты при температуре, равной температуре смеси,
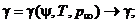 (4.5.4)
(4.5.4)
скорости звука
 (4.5.5)
(4.5.5)
числа Маха
 (4.5.6)
(4.5.6)
температуры торможения
 (4.5.7)
(4.5.7)
среднего значения показателя адиабаты в диапазоне изменения температур от 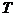 до
до  :
:
 (4.5.8)
(4.5.8)
давления торможения, замеряемого трубкой Пито,
 при
при  , (4.5.9)
, (4.5.9)
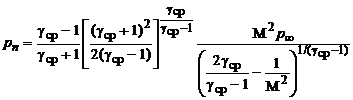 (4.5.10)
(4.5.10)
при 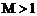
и комплексов 

 На этом процесс вычисления газодинамических параметров по заданным комплексам заканчивается.
На этом процесс вычисления газодинамических параметров по заданным комплексам заканчивается.






