Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и вращательной скорости этой точки вокруг полюса.
Для плоской фигуры совершающей плоскопараллельное движение в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей.
Способы определения мгновенного центра скоростей
1 Если известны прямые, по которым направлены скорости двух точек плоской фигуры А и В,то мгновенный центр скоростей фигуры определится как точка пересечения перпендикуляров к этим прямым, восставленных в точках А и В.
2 Если скорости точек А и В плоской фигуры параллельны между собой и перпендикулярны АВ, и известнымодули скоростей обеих точек А и В то мгновенный центр скоростей расположен на пересечении отрезка соединяющего концы векторов точек А и В с прямой АВ.
3 Если плоская фигура катится без скольжения по некоторой неподвижной кривой то ее мгновенный центр скоростей находится в точке соприкасания данной фигуры с кривой.
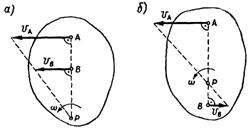
Определение скоростей точек плоской фигуры при помощи мгновенного центра скоростей
Определим скорости точек А, В и К плоской фигуры, приняв за полюс мгновенный центр скоростей Р.
; 
; 
;
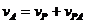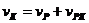Если точка Р является мгновенным центром скоростей, то 
=0, тогда
; 
; 
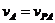т. е. скорость любой точки плоской фигуры в данный момент времени представляет собой вращательную скорость этой точки вокруг мгновенного центра скоростей; поэтому
; 
; 
;
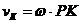Пример
Колесо радиусом R катится без скольжения по прямому рельсу. Скорость центра колеса в рассматриваемый момент времени 
м/с.
Определить скорости точек A, В, D и Е колеса, расположенных на концах взаимно перпендикулярных диаметров.
1-й вариант.
Примем за полюс центр колеса С. Тогда скорость любой точки колеса будет равна геометрической сумме скорости полюса и скорости вращения этой точки вокруг полюса (99.1). Так как колесо катится без скольжения» то скорость точки А касания колеса с рельсом равна нулю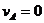 
.
Точка А является мгновенным центром скоростей. В этой точке скорость вращения вокруг полюса 
и скорость полюса 
равны по модулю и противоположны по направлению, т. е.
Расстояния от точек А, В, D, Е до полюса С равны. Следовательно, и вращательные скорости точек вокруг полюса тоже равны, т. е.
Откладывая в каждой точке скорость полюса и вращательную скорость, перпендикулярную соответствующему радиусу колеса, находим:
м/с.
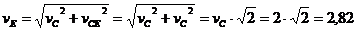м/с.
м/с.
2-й вариант
Примем мгновенный центр скоростей колеса за полюс. Тогда скорости всех точек колеса определятся как вращательные скорости вокруг мгновенного центра скоростей. Модули скоростей всех точек найдутся по пропорциональности скоростей их расстояниям от мгновенного центра скоростей:
Найдем 
Тогда
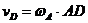
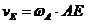
Обозначим радиус колеса через R.
Тогда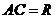 
, 
, 
Тогда
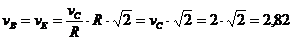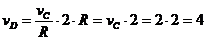м/с
м/с
