—корость - это векторна€ величина, характеризующа€ быстроту и направление движени€ точки в данной системе отсчета.
”скорение точки Ц векторна€ величина, характеризующа€ быстроту изменени€ модул€ и направлени€ скорости точки.
«адание скорости и ускорени€ †точки естественным способом
ѕри задании точки естественным способом известен закон движени€, выраженный зависимостью перемещени€ точки от времени 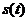
¬ этом случае скорость точки будет определ€тьс€ как перва€ производна€ от данной зависимости

”скорение точки будет определ€тьс€ как втора€ производна€ от зависимости перемещени€ или как перва€ производна€ от зависимости скорости
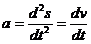
ѕример
“очка движетс€ по окружности радиусом R согласно уравнению.

ќпределить скорость и ускорение точки в конце 3 секунды
 †см/с
†см/с
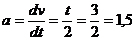 †см/с2
†см/с2
«адание скорости точки координатным способом
ѕри задании точки координатным способом известны законы изменени€ координат данной точки в зависимости от времени  .
.
¬ этом случае скорость точки будет определ€тьс€ как геометрическа€ сумма первых производных от данных зависимостей




”скорение точки будет определ€тьс€ как геометрическа€ сумма первых производных от зависимостей скорости или вторых производных от зависимости изменени€ координат




ѕример
”равнени€ движени€ точки имеют вид


ќпределить уравнени€ скорости и ускорени€ данной точки




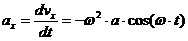


≈сли направление ускорени€ совпадает с направлением скорости (имеет одинаковый знак) то тело движетс€ с положительным ускорением (ускор€етс€), если направление ускорени€ не совпадает с направлением скорости (имеет разные знаки) то тело движетс€ с отрицательным ускорением (замедл€етс€)
ѕоступательное движение
ѕоступательным движением твердого тела называетс€ такое движение, при котором люба€ пр€ма€, соедин€юща€ две точки тела, движетс€ параллельно самой себе.
¬се точки твердого тела, движущегос€ поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорени€.

”равнени€ми поступательного движени€ твердого тела €вл€ютс€ уравнени€ движени€ любой точки этого тела - обычно уравнени€ движени€ его центра т€жести —.
ƒл€ описани€ скорости и ускорени€ точки используютс€ зависимости рассмотренные в предыдущем вопросе.
¬ращательное движение
¬ращательным называетс€ такое движение твердого тела, при котором остаютс€ неподвижными все его точки, лежащие на некоторой пр€мой, называемой осью вращени€.
ѕри этом движении все остальные точки тела движутс€ в плоскост€х, перпендикул€рных оси вращени€, и описывают окружности, центры которых лежат на этой оси.
јналогом перемещени€ во вращательном движении €вл€етс€ угол поворота  †- угол на который повернЄтс€ люба€ точка тела на принадлежаща€ оси вращени€.
†- угол на который повернЄтс€ люба€ точка тела на принадлежаща€ оси вращени€.
¬еличина, характеризующа€ быстроту изменени€ угла поворота с течением времени, называетс€ угловой скоростью тела.
|
|
|
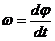
¬еличина, характеризующа€ быстроту изменени€ угловой скорости с течением времени, называетс€ угловым ускорением тела.

¬ращение тела, при котором угловое ускорение посто€нно, называют равнопеременным вращением. ѕри этом, если абсолютна€ величина угловой скорости увеличиваетс€, вращение называют равноускоренным, а если уменьшаетс€ - равнозамедленным.
–ассмотрим движение точки ћ тела †движущуюс€ по окружности с радиусом R.
ќбозначим точку отсчета ќ, и угол, на который повернетс€ эта точка за врем€ t через  .
.
«а врем€ t точка ћ пройдет рассто€ние s равное длине дуги окружности ќћ. Ёто рассто€ние определ€етс€ по формуле.

—корость точки ћ в момент времени t при вращательном движении направлена по касательной к окружности в этой точке и называетс€ окружной скоростью.
¬еличина окружной скорости определ€етс€ из выражени€.



»з предыдущей формулы следует, что модули окружных скоростей различных точек вращающегос€ тела пропорциональны рассто€ни€м от этих точек до оси вращени€.
”скорение точки ћ в момент времени t при вращательном движении складываетс€ из двух составл€ющих вращательного ускорени€ (тангенциального) и центростремительного ускорени€ (нормального).
“ангенциальное ускорение направлено по касательной к окружности в точке ћ.
¬еличина тангенциального ускорени€ определ€етс€ по зависимости

Ќормальное ускорение направлено по радиусу окружности к еЄ центру.
¬еличина нормального ускорени€ определ€етс€ по зависимости

ѕолное ускорение точки определитс€ из выражени€

ѕример
¬ращение маховика в период пуска машины определ€етс€ уравнением
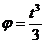
где t - в сек,  †- в рад. ќпределить модуль и направление ускорени€ точки, отсто€щей от оси вращени€ на рассто€нии 50 см, в тот момент, когда ее скорость равна 8 с м/сек.
†- в рад. ќпределить модуль и направление ускорени€ точки, отсто€щей от оси вращени€ на рассто€нии 50 см, в тот момент, когда ее скорость равна 8 с м/сек.
ѕо уравнению вращени€ маховика находим его угловые скорость и ускорение


ќпредел€ем уравнение окружной скорости точки

¬ыражаем отсюда врем€
 с
с
ќпредел€ем
”глова€ скорость  с-1
с-1
”гловое ускорение  с-2
с-2
“ангенциальное ускорение  †м/с2
†м/с2
Ќормальное ускорение 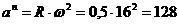 †м/с2
†м/с2
ѕолное ускорение  †м/с2
†м/с2






