1. Измерение может быть проведено в любой шкале.
2. Выборки должны быть случайными и независимыми.
3. Количество наблюдений в выборках должно быть более 30. С увеличением объема выборки точность критерия повышается.
4. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5.
5. Сумма наблюдений по всем интервалам должна быть равна общему количеству наблюдений.
6. Таблица критических значений критерия c2 рассчитана для числа степеней свободы v, которое каждый раз рассчитывается по определенным правилам.
7. Необходимо вносить «поправку на непрерывность» при сопоставлении распределений признаков, которые принимают всего 2 значения. При внесении поправки значение c2 уменьшается.
Алгоритм подсчета критерия c2
Основная расчетная формула критерия c2 выглядит так:
, (12.1)
где fэ j – эмпирические частоты;
fT – теоретическая частота;
k – количество разрядов признака.
Расчеты критерия c2 удобнее заносить в таблицу, состоящую из шести столбцов, в соответствии со следующими шагами:
1. Оформить таблицу, где
· первый столбец – наименования разрядов;
· второй – эмпирические частоты;
· третий – теоретические частоты;
· четвертый – разность между эмпирической и теоретической частотой по каждому разряду (строке);
· пятый – полученные разности в квадрате;
· шестой – результаты деления квадратов разностей на теоретическую частоту.
2. Найти сумму шестого столбца. Полученную сумму обозначить как c2.
3. Определить число степеней свободы v = k- 1, где k – количество разрядов признака. Если сравниваются эмпирические распределения значений, число степеней свободы находится следующим образом: v = (k- 1 ) × (c- 1 ), где k – число строк, а с – число столбцов. Если v= 1, то необходимо внести поправку на «непрерывность».
4. Определить по таблице 8 Приложения 1 критические значения для данного числа степеней свободы v.
5. Для процесса принятия решения вычертить «ось значимости».
Критерий c2 – один из наиболее часто использующихся в психологических исследованиях, поскольку он позволяет решать большое число разных задач.
Рассмотрим ряд примеров решения задач с использованием основной формулы критерия c2 и его модифицированных формул:
· сравнение эмпирического распределения с теоретическим (равномерным) – задача 12.1;
· сравнение эмпирического распределения с теоретическим (нормальным) – задача 12.2;
· сравнение двух эмпирических распределений – задача 12.3;
· сравнение распределений, в случае если признак принимает всего 2 значения (степень свободы v= 1), – задача 12.4;
· сравнение двух эмпирических распределений в выборках одинакового объема с большим количеством переменных – задача 12.5;
· сравнение двух эмпирических распределений в выборках разного объема с большим количеством переменных – задача 12.6.
Задача 12.1
В одной из школ города выяснялась успешность обучения алгебре учащихся десятого класса. Для этого в классе была проведена контрольная работа. Проверялось предположение о равномерном распределении оценок за контрольную работу. Результаты контрольной работы в таблице 12.1.
Таблица 12.1
| Оценки | «5» | «4» | «3» | «2» | Всего взглядов |
| Количество оценок | 14 | 5 | 8 | 5 | 32 |
Необходимо сопоставить полученные эмпирические частоты с теоретическими частотами. Если успеваемость в классе не будет отличаться от равномерного распределения, то количества оценок между «5», «4», «3», «2» будут распределены примерно одинаково.
Решение
Гипотезы к задаче
Н0: Распределение оценок по контрольной работе не отличается от равномерного распределения.
Н1: Распределение оценок по контрольной работе отличается от равномерного распределения.
Теоретическая частота при сопоставлении эмпирического распределения с равномерным определяется по формуле:
fтеор = n / k, (12.2)
где n – количество наблюдений;
k – количество разрядов признака.
Для приведенной задачи fтеор = 32 / 4 = 8. Если бы все оценки распределялись равномерно, то оценку «5» получили бы 8 учащихся, как и оценки «4», «3», «2».
В методе c2 вычисления производятся с точностью до сотых, а иногда и до тысячных долей единицы.
Оформим вычисления расчет критерия c2 при сопоставлении эмпирического распределения оценок по контрольной работе с равномерным распределением в таблицу 12.2.
Таблица 12.2
| Разряды | Эмпирическая частота, f эj | Теоретическая частота, fТ | f эj- fТ | (f эj- fТ)2 | (f эj- fТ)2/ fТ |
| «5» | 14 | 8 | 6 | 36 | 4,50 |
| «4» | 5 | 8 | -3 | 9 | 1,13 |
| «3» | 8 | 8 | 0 | 0 | 0,00 |
| «2» | 5 | 8 | -3 | 9 | 1,13 |
| Сумма | 32 | 32 | 0 | 54 | 6,75 |
Сумма разностей между эмпирическими и теоретической частотами (сумма по четвертому столбцу) всегда равна 0. Если это равенство не соблюдается, это означает, что в подсчете частот или разностей допущена ошибка.
Согласно формуле (12.1) сумма шестого столбца и есть 
.
Для нахождения критических значений критерия c2 необходимо обратиться к таблице 8 Приложения 1, определив предварительно число степеней свободы v. В нашем случае k (число вариантов оценок) = 4, следовательно, v = 4 – 1 = 3. По таблице 8 Приложения 1 находим:
.
Построим «ось значимости». Чем больше отклонения эмпирических частот от теоретических, тем больше будет величина 
. Поэтому «зона значимости» располагается справа, а «зона незначимости» – слева.
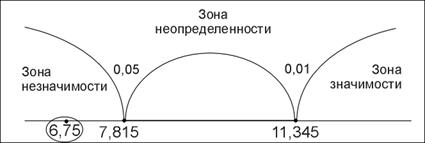
Ответ
c2эмп = 6,75, принимается H0. Распределение оценок по контрольной работе не отличается от равномерного распределения.
При решении задач с равновероятным распределением теоретических частот не было необходимости использовать специальные процедуры их подсчета. Однако на практике чаще возникают задачи, в которых распределение теоретических частот не имеет равновероятного характера. В этих случаях для подсчета теоретических частот используются специальные формулы или таблицы. Рассмотрим задачу, в которой в качестве теоретического будет использоваться нормальное распределение.
Задача 12.2
У 267 человек был измерен рост. Вопрос состоит в том, будет ли полученное в этой выборке распределение роста близко к нормальному (задача взята из учебника Г.Ф. Лакина «Биометрия», 1990).
Данные разбиты на 9 интервалов шириной 3 см. В задаче указаны середины интервалов и эмпирическая частота. Среднее значение 
, стандартное отклонение s = 4,06.
Решение
Гипотезы к задаче
Н0: Распределение роста 267 человек не отличается от нормального.
Н1: Распределение роста 267 человек отличается от нормального.
Для каждого выделенного интервала первоначально подсчитывается нормированные частоты по формуле:
, (12.3)
где xi – середины интервалов;
– среднее;
s – среднеквадратичное отклонение.
Подсчитав эти величины, занесем их в таблицу 12.3, в третий столбец
Затем по величинам нормированных частот по таблице 1 Приложения 1 находим ординаты нормальной кривой – 
, для каждой zi. Ординаты заносим в четвертый столбец таблицы 12.3.
Таблица 12.3
| Центры интервалов xi | Эмпирические частоты fэi |
| Ординаты нормальной кривой
| Расчетные теоретические частоты
|
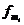
| 155 | 3 | -2,77 | 0,0086 | 1,7 |
| 158 | 9 | -2,03 | 0,0508 | 10,0 |
| 161 | 31 | -1,29 | 0,1736 | 34,3 |
| 164 | 71 | -0,55 | 0,3429 | 67,7 |
| 167 | 82 | 0,19 | 0,3918 | 77,3 |
| 170 | 46 | 0,93 | 0,2589 | 51,1 |
| 173 | 19 | 1,67 | 0,0989 | 19,5 |
| 176 | 5 | 2,41 | 0,0219 | 4,3 |
| 179 | 1 | 3,15 | 0,0028 | 0,6 |
| Сумма | 267 | 267 |
Теоретические частоты находятся по формуле:
, (12.4)
где n – общая величина выборки (n =267);
l – величина интервала (l =3);
s – среднеквадратичное отклонение.
После подсчета эти величины заносятся в пятый столбец таблицы 12.3.
Дальнейшие расчеты проводим на основе стандартной таблицы 12.4.
Согласно формуле (12.1) сумма шестого столбца и есть 
.
Таблица 12.4
| Разряды | Эмпирическая частота, f эj | Теоретическая частота, fТ | f эj- fТ | (f эj- fТ)2 | (f эj- fТ)2/ fТ |
| 155 | 3 | 1,7 | 1,3 | 1,69 | 0,99 |
| 158 | 9 | 10,0 | -1 | 1 | 0,10 |
| 161 | 31 | 34,3 | -3,3 | 10,89 | 0,32 |
| 164 | 71 | 67,7 | 3,2 | 10,24 | 0,15 |
| 167 | 82 | 77,3 | 4,4 | 19,36 | 0,25 |
| 170 | 46 | 51,1 | -5,2 | 27,04 | 0,53 |
| 173 | 19 | 19,5 | -0,4 | 0,16 | 0,01 |
| 176 | 5 | 4,3 | 0,6 | 0,36 | 0,08 |
| 179 | 1 | 0,6 | 0,4 | 0,16 | 0,27 |
| Сумма | 267 | 267 | 0 | 2,7 |
В случае оценки равенства эмпирического распределения нормальному число степеней свободы определяется особым образом: из общего числа интервалов вычитается число 3. В данном случае: 9-3=6. Таким образом, число степеней свободы будет равно v =6. По таблице 8 Приложения 1 находим:
.
«Ось значимости»
Ответ
, принимается Н0. Распределение роста 267 человек не отличается от равномерного.
Задача 12.3
Одинаков ли уровень подготовленности учащихся в классе из задачи 12.1 и в классе, где при изучении этой темы применялась другая методика? Результаты второй группы учащихся представлены в таблице 12.5.
Таблица 12.5
| Оценки | «5» | «4» | «3» | «2» | Всего взглядов |
| Количество оценок | 15 | 6 | 9 | 6 | 36 |
Решение
Гипотезы к задаче
Н0: Распределение оценок по контрольной работе в первой группе учащихся не отличается от распределения оценок во второй группе учащихся.
Н1: Распределение оценок по контрольной работе в первой группе учащихся отличается от распределения оценок во второй группе учащихся.
Для подсчета теоретических частот можно составить специальную таблицу (12.6). Для каждой эмпирической частоты определяется своя теоретическая частота. Это обусловлено тем, что количество учащихся в группах разное и необходимо учитывать эту пропорцию.
Рассчитаем эту пропорцию. Всего оценок в группе получено 68, из них в первой группе – 32 и во второй – 36. Доля оценок в первой группе составит 32/68 = 0,47; доля оценок во второй группе – 36/68 = 0,53.
Таблица 12.6
| Разряды | Эмпирические частоты | Суммы | Теоретические частоты | ||
| В первой группе | Во второй группе | В первой группе | Во второй группе | ||
| «5» | 14 | 15 | 29 | 13,63 | 15,37 |
| «4» | 5 | 6 | 11 | 5,17 | 5,83 |
| «3» | 8 | 9 | 17 | 7,99 | 9,01 |
| «2» | 5 | 6 | 11 | 5,17 | 5,83 |
| Сумма | 32 | 36 | 68 | 32 | 36 |
Итак, во всех строках оценки первой группы должны были бы составлять 0,47 всех оценок по данной строке, а оценки во второй группе – 0,53 всех оценок. Теперь, зная суммы оценок по каждой строке, можно рассчитать теоретические частоты для каждой ячейки таблицы.
Для оценок первой группы:
§ f1 теор = 29×0,47 = 13,63;
§ f2 теор = 11×0,47 = 5,17;
§ f3 теор = 17×0,47 = 7,99;
§ f4 теор = 11×0,47 = 5,17.
Для оценок второй группы:
§ f1 теор = 29×0,53=15,37;
§ f2 теор = 11×0,53=5,83;
§ f3 теор = 17×0,53=9,01;
§ f4 теор = 11×0,53=5,83.
Общая формула подсчета f теор будет выглядеть так:
|
f теор = | Сумма частот по соответствующей строке | . | Сумма частот по соответствующему столбцу |
| Общее количество наблюдений | |||
Теперь оформим вычисление в таблицу 12.7, аналогичную таблице 12.2, представив во втором и третьем столбцах эмпирические и теоретические частоты сначала первой группы, затем второй.
Таблица 12.7
| Ячейки таблицы частот | Эмпирическая частота, f эj | Теоретическая частота, fТ | f эj- fТ | (f эj- fТ)2 | (f эj- fТ)2/ fТ |
| 1 | 14 | 13,63 | 0,37 | 0,137 | 0,010 |
| 2 | 5 | 5,17 | -0,17 | 0,029 | 0,006 |
| 3 | 8 | 7,99 | 0,01 | 0,000 | 0,000 |
| 4 | 5 | 5,17 | -0,17 | 0,029 | 0,006 |
| 5 | 15 | 15,37 | -0,37 | 0,137 | 0,009 |
| 6 | 6 | 5,83 | 0,17 | 0,029 | 0,005 |
| 7 | 9 | 9,01 | -0,01 | 0,0001 | 0,000 |
| 8 | 6 | 5,83 | 0,17 | 0,029 | 0,005 |
| Сумма | 68 | 68 | 0 | 0,041 |
Число степеней свободы при сопоставлении двух эмпирических распределений определяется по формуле (12.3):
v = (k- 1 ) × (с- 1 ), (12.3)
где k – количество разрядов признака (строк в таблице эмпирических частот);
с – количество сравниваемых распределений (столбцов в таблице эмпирических частот).
В данном случае количество разрядов – это количество вариантов оценок, т.е. 4. Количество сопоставляемых распределений с= 2. Итак, для данного случая v = (4-1)× (2-1) =3.
Определяем по таблице Приложения критические значения для v =3:
.
«Ось значимости»
Ответ
, Н0 принимается. Распределение оценок по контрольной работе в первой группе учащихся не отличается от распределения во второй группе учащихся.
Если в задаче требуется сопоставление одновременно трех и более распределений, то принцип расчетов такой же, как и при сопоставлении двух эмпирических распределений.
В случае если число степеней свободы v=1, т. е. если признак принимает всего 2 значения, необходимо вносить поправку на непрерывность.
Задача 12.4 [11]
В исследовании порогов социального атома профессиональных психологов просили определить, с какой частотой встречаются в их записной книжке мужские и женские имена коллег-психологов. Попытаемся определить, отличается ли распределение, полученное по записной книжке женщины-психолога X, от равномерного распределения. Эмпирические частоты представлены в таблицы:
| Мужчин | Женщин | Всего человек |
| 22 | 45 | 67 |
Решение
Гипотезы к задаче
Н0: Распределение мужских и женских имен в записной книжке Х не отличается от равномерного распределения.
Н1: Распределение мужских и женских имен в записной книжке Х отличается от равномерного распределения.
Количество наблюдений n =67; количество значений признака k= 2. Рассчитаем теоретическую частоту:
fтеор = n/ k = 67/2 = 33,5.
Число степеней свободы v = k – 1 =1.
Далее все расчеты производятся по известному алгоритму, но с одним добавлением: перед возведением в квадрат разности частот необходимо уменьшить абсолютную величину этой разности на 0,5. Расчеты внесем в таблицу 12.8.
Таблица 12.8
| Разряды | Эмпирическая частота, f эj | Теоретическая частота, fТ | f эj- fТ | (f эj- fТ-0,5) | (f эj- fТ-0,5)2 | (f э j- fТ-0,5)2 fТ |
| Мужчины | 22 | 33,5 | -11,5 | 11 | 121 | 3,61 |
| Женщины | 45 | 33,5 | 11,5 | 11 | 121 | 3,61 |
| Сумма | 67 | 67 | 0 | 7,22 |
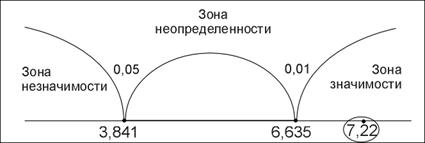
Таким образом, 
=7,22.
Для v =1 определяем по таблице 8 Приложения 1 критические значения:
.
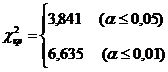«Ось значимости»
Ответ
=7,22, Н0 отклоняется, принимается H1. Распределение мужcких и женских имен в записной книжке психолога Х отличается от равномерного распределения (α<0,01).
Задача 12.5
Психолог сравнивает два эмпирических распределения, в каждом из которых было обследовано 200 человек по тесту интеллекта. Различаются ли между собой эти распределения?
Решение
Гипотезы к задаче
Н0: Распределения уровней интеллекта в двух равных выборках не отличаются между собой.
Н1: Распределения уровней интеллекта в двух равных выборках статистически значимо отличаются между собой.
Представим эмпирические данные в виде таблицы 12.9, в которой приведены также предварительные расчеты, необходимые для получения .
Таблица 12.9
| Уровни интеллекта | Частоты | f1 × f2 | f1+ f2 | f1× f2 f1+ f2 | |
| f1 | f2 | ||||
| 60 | 1 | 1 | 1 | 2 | 0,50 |
| 70 | 5 | 3 | 25 | 8 | 3,13 |
| 80 | 17 | 7 | 289 | 24 | 12,04 |
| 90 | 45 | 22 | 2025 | 67 | 30,22 |
| 100 | 70 | 88 | 4900 | 158 | 31,01 |
| 110 | 51 | 69 | 2601 | 120 | 21,68 |
| 120 | 10 | 7 | 100 | 17 | 5,88 |
| 130 | 1 | 2 | 1 | 3 | 0,33 |
| 140 | 0 | 1 | 0 | 1 | 0,00 |
| Сумма | 200 | 200 | 104,79 | ||
Для случая равенства числа испытуемых в первой и второй выборках расчет производится по формуле (12.4):
, (12.4)
где f1 – частоты первого распределения;
f2 – частоты второго распределения;
n – число элементов в каждой выборке.
Произведем расчет по формуле 12.4, основываясь на результатах таблицы 12.9:
.
В данном случае число степеней свободы v = (k -1 ) ×(c -1) =(9-1) × (2-1) = 8, где k – число интервалов разбиения, а с – число столбцов. В соответствии с таблицей 8 Приложения 1 находим:
.
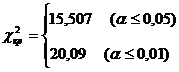«Ось значимости»
Ответ
, принимается Н1. Распределения уровней интеллекта в двух равных выборках статистически значимо отличаются между собой (a<0,05).
Задача 12.6
Психолог сравнивает два эмпирических распределения, в каждом из которых было обследовано по тесту интеллекта разное количество испытуемых. Различаются ли между собой эти распределения?
Решение
Гипотезы к задаче
Н0: Распределения уровней интеллекта в двух неравных выборках не отличаются между собой.
Н1: Распределения уровней интеллекта в двух неравных выборках статистически значимо отличаются между собой.
Представим эмпирические данные в виде таблицы 12.10, в которой приведены также предварительные расчеты, необходимые для получения .
Таблица 12.10
| Уровни интеллекта | Частоты | f1 × f2 | f1+ f2 | f1× f2 f1+ f2 | |
| f1 | f2 | ||||
| 60 | 1 | 0 | 1 | 1 | 1,00 |
| 70 | 8 | 0 | 64 | 8 | 8,00 |
| 80 | 23 | 1 | 529 | 24 | 22,04 |
| 90 | 30 | 11 | 900 | 41 | 21,95 |
| 100 | 38 | 18 | 1444 | 56 | 25,79 |
| 110 | 12 | 14 | 144 | 26 | 5,54 |
| 120 | 7 | 3 | 49 | 10 | 4,90 |
| 130 | 4 | 4 | 16 | 8 | 2,00 |
| 140 | 1 | 1 | 1 | 2 | 0,50 |
| 150 | 0 | 1 | 0 | 1 | 0,00 |
| Сумма | 124 | 53 | 91,72 | ||
В этом случае расчет производится по формуле 12.5:
, (12.5)
где f1 – частоты первого распределения;
f2 – частоты второго распределения;
n1, n2 – число элементов в первой и второй выборках;
N – сумма числа элементов в обеих выборках.
Произведем расчет по формуле 12.5:
.
В данном случае число степеней свободы v = (k -1 ) ×(c -1) =(10-1) × (2-1) = 9, где k – число интервалов разбиения, а с – число столбцов. В соответствии с таблицей 8 Приложения 1 находим:
.
«Ось значимости»
Ответ
, принимается Н1. Распределения уровней интеллекта в двух неравных выборках статистически значимо отличаются между собой (a<0,01).
12.3 l – КРИТЕРИЙ КОЛМОГОРОВА-СМИРНОВА
Назначение критерия l
Критерий l предназначен для решения тех же задач, что и критерий c2 . Иначе говоря, с его помощью можно сравнивать эмпирическое распределение с теоретическим или два эмпирических распределений между собой. Разница между критериями в том, что при применении c2 сопоставляются частоты двух распределений, а при применении критерия l сравниваются накопленные частоты по каждому разряду.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Если различия между двумя распределениями существенны и в какой-то момент разность накопленных частот достигнет критического значения, можно признать различия статистически достоверными. В формулу критерия l включается эта разность. Чем больше эмпирическое значение l, тем более существенны различия.
Гипотезы
Н0: Различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения междуними).
Н1: Различия между двумя распределениями достоверны (судя по точке максимального накопленного расхождения между ними).
Ограничения критерия l Колмогорова-Смирнова
1. Измерение может быть проведено в шкале интервалов и отношений.
2. Выборки должны быть случайными и независимыми.
3. Желательно, чтобы суммарный объем двух выборок был больше или равен 50.
4. Сопоставление эмпирического распределения с теоретическим иногда допускается при n ³5.
5. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака (дни недели, 1-й, 2-й, 3-й месяцы после прохождения курса терапии, повышение температуры тела, усиление чувства недостаточности и т. д.). Во всех тех случаях, когда разряды представляют собой не упорядоченные по возрастанию или убыванию какого-либо признака категории, следует применять метод c2.
Задача 12.7
В выборке учащихся одиннадцатых классов городских школ проводилось тестирование по математике. Распределение результатов тестирования представлено в таблице 12.11.
Таблица 12.11
| Доля правильных ответов, % | Количество учащихся, получивших результат в данном интервале |
| 0-20% | 4 |
| 21-40% | 15 |
| 41-60% | 18 |
| 61-80% | 7 |
| 81-100% | 1 |
Можно ли утверждать, что распределение результатов тестирования по математике учащихся городских школ отличается от равномерного распределения?
Решение
Н0: Эмпирическое распределение результатов тестирования по математике учащихся городских школ не отличается от равномерного распределения.
Н1: Эмпирическое распределение результатов тестирования по математике учащихся городских школ отличается от равномерного распределения.
Эмпирические частости для данного распределения рассчитываются по формуле:
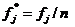, (12.6)
где fj – частота результата в интервале j;
n – общее количество учащихся (наблюдений).
Теоретические частости рассчитываются по формуле:
, (12.7)
где k – количество интервалов (разрядов).
Для нашей задачи
.
Для наглядности расчеты оформим в таблицу 12.12.
Для сопоставления накопленных эмпирических и теоретических частостей находим разность между ними и заносим ее в восьмой столбец.
Определим по восьмому столбцу, какая из абсолютных величин разности является наибольшей. Она будет обозначаться dmax. В данном случае dmax =0,222
Таблица 12.12
| Доля правильных ответов, % | Частота | Частость | Накопленная частость | Разность | |||
| эмпирическая | теоретическая | эмпирическая | теоретическая | эмпирическая | теоретическая | ||
| 0-20% | 4 | 9 | 0,089 | 0,200 | 0,089 | 0,200 | -0,111 |
| 21-40% | 15 | 9 | 0,333 | 0,200 | 0,422 | 0,400 | 0,022 |
| 41-60% | 18 | 9 | 0,400 | 0,200 | 0,822 | 0,600 | 0,222 |
| 61-80% | 7 | 9 | 0,156 | 0,200 | 0,978 | 0,800 | 0,178 |
| 81-100% | 1 | 9 | 0,022 | 0,200 | 1,000 | 1,000 | 0,000 |
| Сумма | 45 | 45 | 1 | 1 | 0,533 | ||
Теперь необходимо обратиться к таблице 9 Приложения 1 для определения критических значений dmax при n =45:
.
«Ось значимости»
Ответ
dmax =0,222, принимается Н1. Эмпирическое распределение результатов тестирования по математике учащихся городских школ отличается от равномерного распределения (при a<0,05).
Задача 12.8
В выборке учащихся одиннадцатых классов районных школ проводилось тестирование по математике при помощи теста, аналогичного тесту для городских школ (задача 12.7). Распределение результатов тестирования представлено в таблице 12.13.
Таблица 12.13
| Доля правильных ответов, % | Количество учащихся, получивших результат в данном интервале |
| 0-20% | 5 |
| 21-40% | 11 |
| 41-60% | 5 |
| 61-80% | 4 |
| 81-100% | 0 |
Можно ли утверждать, что распределение результатов тестирования по математике учащихся городских школ отличается от распределения результатов учащихся районных школ?
Решение
Гипотезы к задаче
Н0: Распределение результатов тестирования по математике учащихся городских школ не отличается от распределения результатов учащихся районных школ.
Н1: Распределение результатов тестирования по математике учащихся городских школ отличается от распределения результатов учащихся районных школ.
Поскольку в данной задаче сопоставляются накопленные эмпирические частости по каждому разряду, то теоретические частости не вычисляются.
Критерий l находится по формуле:
, (12.7)
где п1 – количество наблюдений в первой выборке;
n2 – количество наблюдений во второй выборке;
dmax – наибольшее из абсолютных величин разности накопленных эмпирических частостей.
По таблице 10 Приложения 1 определить, какому уровню статистической значимости a соответствует полученное значение l. Если l> 1,36, различия между распределениями можно считать достоверными. Последовательность выборок может быть выбрана произвольно.
Основные расчеты для нашей задачи оформляются в таблицу 12.14.
Максимальная разность между накопленными эмпирическими частостями составляет 0,218 и попадает на второй разряд.
Таблица 12.14
| Доля пра-вильных ответов, % | Эмпирические частоты | Эмпирические частости | Накопленные эмпирические частости | Разность | |||
| f 1 | f2 | f1* | f2* | S f1* | S f2* | S f1*- S f2* | |
| 0-20% | 4 | 5 | 0,089 | 0,200 | 0,089 | 0,200 | 0,111 |
| 21-40% | 15 | 11 | 0,333 | 0,440 | 0,422 | 0,640 | 0,218 |
| 41-60% | 18 | 5 | 0,400 | 0,200 | 0,822 | 0,840 | 0,018 |
| 61-80% | 7 | 4 | 0,156 | 0,160 | 0,978 | 1,000 | 0,022 |
| 81-100% | 1 | 0 | 0,022 | 0 | 1,000 | 1,000 | 0 |
| Сумма | 45 | 25 | 1 | 1 | |||
В соответствии с формулой подсчитываем lэмп по формуле (12.7):
.
По таблице 10 Приложения 1 определяем уровень статистической значимости полученного значения: a =0,59.
«Ось значимости»
На оси указаны критические значения l, соответствующие принятым уровням значимости: l0,05 =1,36, l0,01 =1,63.
Ответ
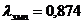, принимается H0. Распределение результатов тестирования по математике учащихся городских школ не отличается от распределения результатов учащихся районных школ.
12.4 КРИТЕРИЙ j * - УГЛОВОЕ ПРЕОБРАЗОВАНИЕ ФИШЕРА
Многофункциональные статистические критерии – это критерии, которые могут использоваться по отношению к самым разнообразным данным, выборкам и задачам. С помощью этого рода критериев можно решать задачи на сопоставление уровней исследуемого признака, сдвигов и сравнение распределений. При этом данные могут быть представлены в любой шкале, выборки могут быть независимые и связанные.
К многофункциональным статистическим критериям относятся угловое преобразование Фишера (j* критерий Фишера), применяемое в случае наличия двух выборок, и биноминальный критерий m для задач с одной выборкой.
Применение многофункциональных критериев позволяет определить, какая доля наблюдений в данной выборке характеризуется интересующим нас эффектом и какая доля этим эффектом не характеризуется.
В качестве эффектов могут выступать:
§ качественные признаки (выражение согласия с предложением, выбор правой дорожки из двух и т.д.);
§ количественные признаки (уровень оценки, превышающий проходной балл, решение задачи менее чем за 20 секунд и т.п.);
§ соотношение значений или уровней признаков (преимущественное появление крайних признаков).
Назначение критерия j*
Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.
Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий исследователя эффект.
Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол j, меньшей доле – меньший угол, но соотношения здесь нелинейные:
,
где Р – процентная доля, выраженная в долях единицы.
При увеличении расхождения между углами j1 и j2 и увеличении численности выборок значение критерия возрастает. Чем больше величина j*, тем более вероятно, что различия достоверны.
Критерии j * используется часто в сочетании с критерием l Колмогорова-Смирнова в целях достижения максимально точного результата.
Гипотезы
Н0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.
Н1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.
Условия применения критерия j*
1. Измерение может быть проведено в любой шкале.
2. Характеристики выборок могут быть любыми.
3. Ни одна из сопоставляемых долей не должна быть равной нулю.
4. Нижняя граница – в одной из выборок может быть только 2 наблюдения, при этом во второй должно быть не менее 30 наблюдений. Верхняя граница не определена.
5. Должны соблюдаться следующие соотношения в численности двух выборок:
§ если n1 = 2, то n2 ³ 30;
§ если n1 = 3, то n2 ³ 7;
§ если n1 = 4, то n2 ³ 5;
§ если n1 ³ 5, то n2 ³ 5 (любые сочетания).
Задача 12.8
Психолог провел эксперимент, в котором выяснилось, что из 20 учащихся с экспериментальной задачей справились 11 (55%) человек, а из 25 человек второй группы успешно справились с задачей 10 (40%). Различаются ли две группы учащихся по успешности решения новой экспериментальной задачи?
Решение
Гипотезы к задаче
Н0: Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй.
Н1: Доля лиц, справившихся с задачей, в первой группе больше, чем во второй.
По таблице 11 Приложения 1 находим величины j1 и j2, соответствующие процентным долям в каждой группе:
j1 (55%)=1,671,
j2 (40%)=1,369.
Подсчитаем эмпирическое значение j* по формуле (12.8):
, (12.8)
где j1 – угол, соответствующий большей процентной доле;
j2 – угол, соответствующий меньшей процентной доле;
n 1 – количество наблюдений в выборке 1;
n 2 – количество наблюдений в выборке 2.
В нашем случае
.
По таблице 12 Приложения 1 определяется, что 
= 1,007 соответствует уровню значимости a >0,10.
Можно установить и критические значения 
, соответствующие принятым в психологии уровням статистической значимости:
.
«Ось значимости»
Ответ
= 1,007, принимается H0. Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй.
Критерий Фишера с равным успехом может использоваться и при сравнении распределений количественных признаков. В данном варианте использования критерия сравнивается процент испытуемых в одной выборке, которые достигают определенного уровня значения признака, с процентом испытуемых, достигающих этого уровня, в другой выборке.
Задача 12.9
Будет ли уровень тревожности у подростков-сирот более высоким, чем у сверстников из полных семей?
Для решения этой задачи психолог проводил анализ выраженности уровня тревожности в группе сирот и в группе детей из полных семей при помощи опросника Тейлора. 40 баллов и выше рассматривались как показатель высокой тревожности (Практическая психодиагностика: Методики и тесты. – Изд-во БАХРАХ-М.2000.С.164)
Решение
В первой группе из 10 человек очень высокий уровень тревожности наблюдался у 7 испытуемых (70%), во второй группе из 13 человек он был обнаружен у 3 испытуемых (23,1%). Можно ли считать подобные различия статистически значимыми?
Гипотезы к задаче
Но: Доля лиц с высоким уровнем тревожности, в первой группе детей не больше, чем во второй.
Н1: Доля лиц с высоким уровнем тревожности, в первой группе детей больше, чем во второй.
По таблице 11 Приложения 1 определяем величины j, соответствующие процентным долям «эффекта» в каждой из групп:
j1 (70%)=1,982,
j2 (23,1%)=1,003.
Подсчитываем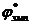 
по формуле (12.8):
.
Критические величины этого критерия нам уже известны:
.
«Ось значимости»
Ответ
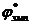= 2,32, принимается H1. Доля лиц с высоким уровнем тревожности, в первой группе детей больше, чем во второй.
Если выборки сопоставляются по каким-либо количественно измеренным показателям, встает проблема выявления той точки распределения, которая может использоваться как критическая при разделении всех испытуемых на тех, у кого «есть эффект», и тех, у кого «нет эффекта».
Для того чтобы максимально повысить мощность критерия j*, нужно выбрать точку, в которой различия между двумя сопоставляемыми группами являются наибольшими. Точнее всего мы сможем сделать это с помощью алгоритма расчета критерия l, позволяющего обнаружить точку максимального расхождения между двумя выборками.
Рассмотрим задачу, демонстрирующую использование критерия j* в сочетании с критерием l Колмогорова-Смирнова.
Задача 12.10
Рассмотрим решение задачи 12.8 с момента определения максимальной разности между двумя накопленными эмпирическими частостями.
Максимальная разность dmax =0,218 оказывается накопленной во второй категории результатов. Попробуем использовать верхнюю границу данной категории в качестве критерия для разделения обеих выборок на подгруппу, где «есть эффект», и подгруппу, где «нет эффекта».
Будем считать, что «эффект есть», если данный учащийся получил результат от 41 до 100%, и «эффекта нет», если данный учащийся получил от 0 до 40%.
Полученное распределение результатов представлено в таблице 12.16:
Таблица 12.16
Доля правильных ответов, % | Эмпирические частоты выбора данной категории результата | ||
| Учащиеся городских школ (n1 =45) | Учащиеся районных школ (n2 =25) | Суммы | |
| от 0 до 40% | 19 | 16 | 35 |
| от 41 до 100% | 26 | 9 | 35 |
| Суммы | 45 | 25 | 70 |
Полученную таблицу мы можем использовать, проверяя разные гипотезы путем сопоставления любых двух ее ячеек.
Доля лиц, получивших результат в пределах от 41 до 100%, среди учащихся городских школ составляет 57,8% (26/45=0,578), среди учащихся районных школ – 36% (9/25=0,36).
Для применения критерия j* переформулируем вопрос в нашей задаче: можно ли считать, что доля учащихся, получивших результат в пределах 41-100%, среди учащихся городских школ больше, чем среди учащихся районных школ?
Гипотезы к задаче
Н0: Доля учащихся, получивших результат в пределах 41-100%, среди учащихся городских школ не больше, чем среди учащихся районных школ.
Н1: Доля учащихся, получивших результат в пределах 41-100%, среди учащихся городских школ больше, чем среди учащихся районных школ.
По таблице определяем величины j, соответствующие процентным долям «эффекта» в каждой из групп:
j1 (57,8%)=1,727,
j2 (36,0%)=1,287.
Подсчитываем 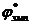по формуле 12.8:
.
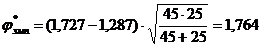Критические величины этого критерия:
.
«Ось значимости»
Ответ
j*эмп =1,764, Н0 отвергается. Доля учащихся, получивших результат в пределах 41-100%, среди учащихся городских школ больше, чем среди учащихся районных школ (a=0,039).
? ВОПРОСЫ И УПРАЖНЕНИЯ
1. Перечислите типы задач, которые решаются с помощью критерия c2 Пирсона.
2. Перечислите ограничения, которые накладывают на выборки данных следующие критерии: c2 Пирсона, l Колмогорова-Смирнова, угловое преобразование Фишера.
3. В эксперименте испытуемый должен произвести выбор левого или правого стола с заданиями. В инструкции психолог подчеркивает, что задания на обоих столах одинаковы. Из 150 испытуемых правый стол выбрали 94 человека, а левый 56. Можно ли утверждать, что подобный выбор левого или правого стола равновероятен, или он обусловлен какой-либо причиной, неизвестной психологу?
 |
ЗАКЛЮЧЕНИЕ
 |
Изучение методов многомерного анализа – следующая ступень применения математических методов в психологии, не вошедшая в это пособие.
Можно выделить две основные причины, связанные со спецификой психологических явлений, приводящие к необходимости использовать сложные математические методы в их изучении:
§ многосторонность психологических явлений, которая вынуждает исследователя использовать систему показателей;
§ невозможность прямого замера многих психологических явлений и использование для этого косвенных показателей.
Применяя на практике систему показателей нескольких психологических явлений, психолог сталкивается с задачей объяснить и интерпретировать структуру связи психологических переменных. При этом перед исследователем могут встать следующие задачи.
Во-первых, установить факты непосредственных связей психологических явлений и их направление. Для этого используют регрессионный и дисперсионный анализы.
Регрессионный анализ, имеет своей целью, связать одну конкретную психологическую переменную c другой.
Дисперсионный анализ – система статистических методов исследования влияния независимых качественных переменных (факторов) на изучаемую зависимую количественную переменную по дисперсии.
Во-вторых, выявить факты парных связей и установить глубинные групповые взаимосвязи между психологическими явлениями. Для этого используют корреляционный, факторный, кластерный и дискриминантный анализы.
Корреляционный анализ, главное назначение которого – выявить взаимовлияние психологических переменных между собой, был описан в теме 9 данного пособия.
Факторный анализ – метод статистического анализа психологической информации, применяемый при исследовании статистически связанных признаков с целью выявления латентных факторов.
Дискриминантный анализ – метод многомерной статистики для различения (дифференциации) и диагностирования психологических явлений, отличия между которыми не очевидны.
Кластерный анализ – это математическая процедура многомерного анализа нахождения «расстояния» (меры различия) между объектами по всей совокупности параметров и изображения их отношений графически. Смысл кластеризации состоит в последовательном объединении объектов в так называемые кластеры, т.е. группы, где сходства между объектами выше, чем с другими объектами или кластерами – группами объектов.
Латентной переменной (фактором) называется величина, которую непосредственно измерить нельзя и для которой не известны уравнения связи с какими-либо явными переменными. Большинство психических явлений, безусловно, должно рассматриваться как латентные переменные. Во многих случаях мы не знаем о них ничего, кроме того, что они существуют и, обусловливая жизнедеятельность, проявляются в действиях (реакциях) индивида. Сами эти действия представляют собой явные переменные, так как их можно объективно измерить, прямо или косвенно.
Явной переменной называется величина, которую можно непосредственно или косвенно измерить. Например, можно непосредственно измерить длительность зрительно-моторной реакции секундомером. Величину процесса торможения в коре головного мозга можно косвенно измерить посредством электроэнцефалограммы. Длительность зрительно-моторной реакции, величина процесса торможения – это явные переменные. Отметим, что при косвенных измерениях переменной X через переменную Y должно быть известно в явном виде уравнение X = f(Y). Причем, явная или латентная переменная – это переменная, которую мы хотим оценить. Такую переменную называют зависимой переменной, или откликом. Переменная, используемая для оценки отклика, называется независимой переменной, или фактором.
Основная функция методов многомерного анализа – выявление скрытой, или латентной, структурыпсихологического явления, выступающей в качестве модели.
ПРИЛОЖЕНИЕ 1
Статистические таблицы критических значений
|
Таблица 1
Значение функции 
(ординаты единичной нормальной кривой)
| x | Сотые доли х | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 3989 | 3989 | 3989 | 3988 | 3986 | 3984 | 3982 | 3980 | 3977 | 3973 |
| 0,1 | 3970 | 3965 | 3961 | 3956 | 3951 | 3945 | 3939 | 3932 | 3925 | 3918 |
| 0,2 | 3910 | 3902 | 3894 | 3885 | 3876 | 3867 | 3857 | 3847 | 3836 | 3825 |
| 0,3 | 3814 &n | |||||||||
