Суть данного метода заключается в том, что частные критерии Fi (X), i =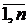 
каким-либо образом объединяются в один интегральный критерий F (X) = Ф (F 1 (X), F 2 (X),…, Fn (X)), а затем находится максимум или минимум данного критерия.
Если объединение частных критериев производится, исходя из объектной взаимосвязи частных критериев и критерия обобщенного, то тогда оптимальное решение будет корректно. Но такое объединение осуществить крайне сложно или невозможно, поэтому, как правило, обобщенный критерий есть результат чисто формального объединения частных критериев.
В зависимости от того, каким образом частные критерии объединяются в обобщенный критерий различают следующие виды обобщенных критериев:
1) аддитивный критерий;
2) мультипликативный критерий;
3) максиминный (минимаксный) критерий.
Аддитивный критерий. В этом случае целевая функция получается путем сложения нормированных значений частных критериев. В общем виде целевая функция имеет следующий вид:
,
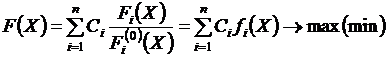где n – количество объединяемых частных критериев; Ci – весовой коэффициент i -го частного критерия; Fi (X) – числовое значение i -го частного критерия; Fi (0) (X) – i -й нормирующий делитель; fi (X) – нормированное значение i -го частного критерия.
Частные критерии имеют различную физическую природу и поэтому различную размерность. А значит просто суммировать их некорректно. В связи с этим в предыдущей формуле числовые значения частных критериев делятся на некоторые нормирующие делители, которые назначается следующим образом:
- в качестве нормирующих делителей принимаются директивные значения параметров или критериев, заданные заказчиком. Считается, что значения параметров, заложенные в техническом задании, являются оптимальными или наилучшими;
- в качестве нормирующих делителей принимаются максимальные (минимальные) значения критериев, достигаемые в области допустимых решений.
Размерности самих частных критериев и соответствующих нормирующих делителей одинаковы, поэтому в итоге обобщенный аддитивный критерий получается безразмерной величиной.
Преимущество аддитивного критерия: как правило, всегда удается определить единственный оптимальный вариант решения.
Недостатки:
- трудности (субъективизм) в определении весовых коэффициентов;
- аддитивный критерий не вытекает из объектной роли частных критериев и поэтому выступает как формальный математический прием;
- в аддитивном критерии происходит взаимная компенсация частных критериев, т. е. уменьшение одного из них может быть компенсировано увеличением другого критерия.
Пример. Определить оптимальный вариант машины с использованием обобщенного (интегрального) аддитивного критерия. Частными критериями, с помощью которых оценены варианты машины, являются ее производительность и надежность (наработка на отказ). Оба критерия «работают» на максимум, т. е. наилучшими вариантами машины являются те из них, которые обеспечивают наибольшую ее производительность и надежность. Исходные данные для решения задачи приведены в таблице 3.2.
Таблица 3.2 – Исходные данные для определения
оптимального варианта исполнения машины
| Критерий Fi | Весовой | Значения критериев для вариантов | ||
| Вариант 1 | Вариант 2 | Вариант 3 | ||
| Производительность F 1, шт/ч | 0,6 | 1000 | 2000 | 4000 |
| Надежность (наработка на отказ) F 2, ч | 0,4 | 1500 | 1000 | 500 |
Целевая функция на основе аддитивного критерия запишется следующим образом:
.
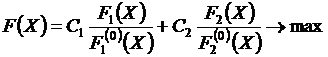В качестве нормирующих делителей в данной задаче примем наилучшие (максимальные) значения частных критериев:
F 1(0) (X) = 4000 шт/ч, F 2(0) (X) = 1500 шт/ч.
Значения обобщенного аддитивного критерия рассчитываются для каждого варианта машины.
Вариант 1. F (X) = 0,6(1000/4000) + 0,4(1500/1500) = 0,55.
Вариант 2. F (X) = 0,6(2000/4000) + 0,4(1000/1500) = 0,558.
Вариант 3. F (X) = 0,6(4000/4000) + 0,4(500/1500) = 0,732.
Оптимальным является 3 вариант машины, т. к. ему соответствует максимальное значение обобщенного аддитивного критерия.
Один из недостатков этого метода заключается в том, что весовые коэффициенты назначает проектировщик. Разные проектировщики могут назначать разные весовые коэффициенты. Пусть, например, C 1 = 0,4;
C 2 = 0,6. Определим теперь значения аддитивных критериев для вариантов машины.
Вариант 1. F (X) = 0,4 × 0,25 + 0,6 × 1 = 0,7.
Вариант 2. F (X) = 0,4 × 0,5 + 0,6 × 0,67 = 0,602.
Вариант 3. F (X) = 0,4 × 1 + 0,6 × 0,33 = 0,598.
Таким образом, при изменении значений весовых коэффициентов оптимальным уже будет 1 вариант машины.
Мультипликативный критерий. В данном случае целевая функция здесь записывается следующим образом:
,
где П – знак произведения; С i – весовой коэффициент i -го частного критерия; Fi (X) – числовое значение i -го частного критерия.
Преимущества мультипликативного критерия:
- не требуется нормирование частных критериев;
- практически всегда определяется одно оптимальное решение.
Недостатки:
- трудности (субъективизм) в определении весовых коэффициентов частных критериев;
- перемножение разных размерностей;
- взаимная компенсация значений частных критериев.
Максиминный (минимаксный) критерий. Эти критерии работают по принципу компромисса, который основывается на идее равномерности. Сущность принципа максимина заключается в следующем. При проектировании сложных систем, при наличии большого числа частных критериев установить между ними аналитическую взаимосвязь очень сложно. Поэтому стараются найти такие значения переменных (параметров) X = { x 1, x 2,…, xm }, при которых нормированные значения всех частных критериев равны между собой:
Cifi (X) = K,
где Ci – весовой коэффициент i -го частного критерия; fi (X) – нормированное значение i -го частного критерия; K – константа.
При большом количестве частных критериев из-за сложных взаимосвязей добиться выполнения указанного выше соотношения очень сложно. Поэтому на практике так варьируют значениями переменных проектирования x 1, x 2,…, xm, при которых последовательно «подтягиваются» те нормированные критерии, численные значения которых в исходном решении оказались наименьшими. Т. к. эта операция производится в области компромисса, подтягивание «отстающего» критерия неизбежно приводит к снижению значений части остальных критериев. Но при проведении
ряда шагов можно добиться определенной степени уравновешивания противоречивых частных критериев, что и является целью принципа максимина.
Формально принцип максимина формулируется следующим образом: выбрать такой набор переменных Х (0) Î Х, при котором реализуется максимум из минимальных нормированных значений частных критериев,
т. е. F (X (0)) = max min fi (X).
Такой принцип выбора Х (0) иногда носит название гарантированного результата. Он заимствован из теории игр, где является основным принципом.
Если частные критерии необходимо минимизировать, то самым отстающим критерием является тот, который принимает максимальное значение. В этом случае применяют принцип минимакса:
F (X (0)) = min max fi (X)
