Случайный процесс, протекающий в системе, называется Марковским, если для любого момента времени t 0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t 0 и не зависят от того, когда и как система пришла в это состояние.
Пусть в настоящий момент t 0 система находится в определенном состоянии S 0. Известны характеристики состояния системы в настоящем t 0 ® S 0 и всё, что было при t < t 0 (предысторию процесса). Возможно ли предугадать (предсказать) будущее, т. е. что будет при t > t 0? В точности – нет, но какие-то вероятностные характеристики процесса в будущем можно определить. Например, вероятность того, что через некоторое время t система S окажется в состоянии S 1 или останется в состоянии S 0 и т. д.
Пример. Система S – группа самолетов, участвующих в воздушном бою. Пусть x – количество «красных» самолетов, y – количество «синих» самолетов. К моменту времени t 0 количество сохранившихся (не сбитых) самолетов соответственно x 0 и y 0. Интересует вероятность того, что в момент времени (t 0 + t) численный перевес будет на стороне «красных». Эта вероятность зависит от того, в каком состоянии находилась система в момент времени t 0, а не от того, когда и в какой последовательности погибали сбитые до момента t 0 самолеты.
На практике Марковские процессы в чистом виде обычно не встречаются. Но имеются процессы, для которых влиянием «предыстории» можно пренебречь. При изучении таких процессов можно применять Марковские модели (в теории массового обслуживания рассматриваются и не Марковские системы массового обслуживания, но математический аппарат, их описывающий, гораздо сложнее).
В теории массового обслуживания большое значение имеют Марковские случайные процессы с дискретными состояниями и непрерывным временем.
Процесс называется процессом с дискретным состоянием, если его возможные состояния S 1, S 2, … можно заранее определить, и переход системы из состояния в состояние происходит «скачком», т. е. практически мгновенно.
Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а неопределенны, случайны и могут произойти в любой момент.
Пример. Технологическая система (участок) S состоит из двух станков, каждый из которых в случайный момент времени может выйти из строя (отказать), после чего мгновенно начинается ремонт узла, тоже продолжающийся заранее неизвестное, случайное время. Возможны следующие состояния системы: S 0 – оба станка исправны; S 1 – первый станок ремонтируется, второй исправен; S 2 – второй станок ремонтируется, первый исправен; S 3 – оба станка ремонтируются.
Переходы системы S из состояния в состояние происходят практически мгновенно, в случайные моменты выхода из строя того или иного станка или окончания ремонта.
| При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой – графом состояний. Вершины графа – состояния системы. Дуги графа – возможные переходы из состояния в состояние (рис. 4.1). Примечание. Переход из состояния S 0 в S 3 на рисунке не обозначен, т. к. предполагается, что станки выходят из строя независимо друг от друга. Вероятностью одновременного выхода из строя обоих станков можно пренебречь. |
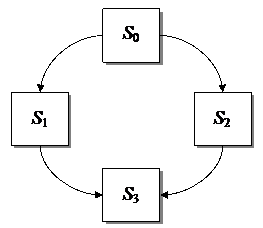Рис. 4.1. Граф состояний системы
|
Потоки событий
Поток событий – последовательность однородных событий, следующих одно за другим в случайные моменты времени.
Примерами потоков событий могут быть: поток отказов и поток восстановлений, поток вызовов на телефонной станции, поток покупателей в магазине и т. д.
Поток событий можно наглядно изобразить рядом точек на оси времени Ot (рис. 4.2).
Рис. 4.2. Распределение событий на оси времени
Интенсивность потока событий (l) – это среднее число событий, приходящееся на единицу времени.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность l стационарного потока постоянна. Поток событий неизбежно имеет сгущения или разрежения, но они не носят закономерного характера, и среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.
Поток событий называется потоком без последствий, если для любых двух непересекающихся участков времени t1 и t2 число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами.
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу.
Поток событий называется простейшим ( или стационарным пуассоновским ), если он обладает сразу тремя свойствами: 1) стационарен, 2) ординарен, 3) не имеет последствий.
Простейший поток имеет наиболее простое математическое описание. Он играет среди потоков такую же особую роль, как и закон нормального распределения среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.
Для простейшего потока с интенсивностью l интервал T между соседними событиями имеет так называемое показательное (экспоненциальное) распределение с плотностью
f (t) = l e – l t,
где l – параметр показательного закона.
Для случайной величины X, имеющей показательное распределение, математическое ожидание M (X) есть величина, обратная параметру, а стандартное (среднее квадратичное) отклонение s(X) равно математическому ожиданию:
M (X) = s(X) = 1/l.
