Требования к презентации
На первом слайде размещается:
название презентации;
автор: ФИО, группа, название учебного учреждения (соавторы указываются в алфавитном порядке);
год.
На втором слайде указывается содержание работы, которое лучше оформить в виде гиперссылок (для интерактивности презентации).
На последнем слайде указывается список используемой литературы в соответствии с требованиями, интернет-ресурсы указываются в последнюю очередь.
| Оформление слайдов | |
| Стиль | необходимо соблюдать единый стиль оформления; нужно избегать стилей, которые будут отвлекать от самой презентации; вспомогательная информация (управляющие кнопки) не должны преобладать над основной информацией (текст, рисунки) |
| Фон | для фона выбираются более холодные тона (синий или зеленый) |
| Использование цвета | на одном слайде рекомендуется использовать не более трех цветов: один для фона, один для заголовков, один для текста; для фона и текста используются контрастные цвета; особое внимание следует обратить на цвет гиперссылок (до и после использования) |
| Анимационные эффекты | нужно использовать возможности компьютерной анимации для представления информации на слайде; не стоит злоупотреблять различными анимационными эффектами; анимационные эффекты не должны отвлекать внимание от содержания информации на слайде |
| Представление информации | |
| Содержание информации | следует использовать короткие слова и предложения; время глаголов должно быть везде одинаковым; следует использовать минимум предлогов, наречий, прилагательных; заголовки должны привлекать внимание аудитории |
| Расположение информации на странице | предпочтительно горизонтальное расположение информации; наиболее важная информация должна располагаться в центре экрана; если на слайде располагается картинка, надпись должна располагаться под ней. |
| Шрифты | для заголовков не менее 24; для остальной информации не менее 18; шрифты без засечек легче читать с большого расстояния; нельзя смешивать разные типы шрифтов в одной презентации; для выделения информации следует использовать жирный шрифт, курсив или подчеркивание того же типа; нельзя злоупотреблять прописными буквами (они читаются хуже, чем строчные). |
| Способы выделения информации | Следует использовать: рамки, границы, заливку разные цвета шрифтов, штриховку, стрелки рисунки, диаграммы, схемы для иллюстрации наиболее важных фактов |
| Объем информации | не стоит заполнять один слайд слишком большим объемом информации: люди могут единовременно запомнить не более трех фактов, выводов, определений. наибольшая эффективность достигается тогда, когда ключевые пункты отражаются по одному на каждом отдельном слайде. |
| Виды слайдов | Для обеспечения разнообразия следует использовать разные виды слайдов: с текстом, с таблицами, с диаграммами. |
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
1. Цель работы
2. Задание
3. Выполненная практическая работа в соответствии с заданием
4. Ответы на контрольные вопросы
5. Вывод
Контрольные вопросы:
1. Запишите основную задачу численного интегрирования.
2. Запишите основные формулы интегрирования.
3. Запишите формулу трапеций.
4. Запишите формулу прямоугольников.
5. Запишите формулу Симпсона.
ПРАКТИЧЕСКАЯ РАБОТА №18
Тема: Решение задач на нахождение по таблично заданной функции (при п=2), заданной аналитически.
Цель работы: Закрепить и систематизировать знания по теме «Основные численные методы».
Задание: Составить таблицу конечных разностей функций, заданных аналитически, от начального значения х0 до конечного х7, приняв шаг равным h:
| 1. | 3. 
| 4. |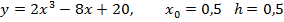 
|
| 2. | 3. 
| 5. | 
|
| 3. | 7. 
| 6. | 
|
Задание: Построить таблицу разностей функции 
, заданной таблично:
| 7. |
| 10. |
| ||||||||||||||||||||||||||||||||
| 8. |
| 11. |
| ||||||||||||||||||||||||||||||||
| 9. |
| 12. |
|
Задание: Найти значения первой и второй производных функции, заданной таблично, в точках x = a + bn:
| 13. | x=2,4+0,05n
n=1 | ||||||||||||||
| 14. | x=4,5-0,06n
n=5 | ||||||||||||||
| 15. | x=1,6+0,08n
n=2 | ||||||||||||||
| 16. | x=2,4+0,05n
n=3 | ||||||||||||||
| 17. | x=4,5-0,06n
n=7 | ||||||||||||||
| 18. | x=1,6+0,08n
n=4 |
Задание: По табличным данным найти аналитическое выражение первой производной:
| 19. |
| ||||||||||||||||||||
| 20. |
| ||||||||||||||||||||
| 21. |
| ||||||||||||||||||||
| 22. |
| ||||||||||||||||||||
| 23. |
| ||||||||||||||||||||
| 24. |
|
Задание: Вычислить значения первой и второй производной функции в точке 
, методом численного дифференцирования. Вычисления вести с четырьмя знаками после запятой:
| 25. |
| ||||||||||||||||||||
| 26. |
| ||||||||||||||||||||
| 27. |
| ||||||||||||||||||||
| 28. |
| ||||||||||||||||||||
| 29. |
| ||||||||||||||||||||
| 30. |
|
Пояснения к работе:
Необходимые формулы:
Задача численного дифференцирования состоит в приближенном вычислении производных функции f(x) по заданным в конечном числе точек значениям этой функции.
Один из универсальных способов построения формул численного дифференцирования состоит в том, что по значениям функции f(x) в некоторых узлахx0, x1,..., xN строят интерполяционный полином PN(x) (обычно в форме Лагранжа) и приближенно полагают f (r)(x) ≈P(r)N(x),
0 ≤ r ≤ N
В ряде случаев наряду с приближенным равенством удается (например, используя формулу Тейлора) получить точное равенство, содержащее остаточный член R (погрешность численного дифференцирования):
f (r) (x) = P(r)N(x) + R, 0 ≤ r ≤ N
Такие формулы называются формулами численного дифференцирования с остаточными членами. Степень, с которой входит величина 
(hi=xi - xi-1) в остаточный член, называется порядком погрешности формулы численного дифференцирования. Формулы с отброшенными остаточными членами называются просто формулами численного дифференцирования.
Формулы численного дифференцирования с остаточными членами для первой (r=1) и второй (r=2) производных в узлах, расположенных с постоянным шагом hi≡h > 0:
r=1, N=1 (два узла): f '(x0) = (f1 - f0)/h - hf ''(ξ)/2
f '(x1) = (f1 - f0)/h + hf ''(ξ)/2
r=1, N=2 (три узла): f '(x0) = (-3f0 + 4f1 - f2)/2h + h2f '''(ξ)/3
f '(x1) = (f2 - f0)/2h - h2f '''(ξ)/6
f '(x2) = (f0 - 4f1 + 3f2)/2h + h2f '''(ξ)/3
r=2, N=2 (три узла): f ''(x0) = (f0 - 2f1 + f2)/h2 - hf '''(ξ)
f ''(x1) = (f0 - 2f1 + f2)/h2 - h2f (4) (ξ)/12
f ''(x2) = (f0 - 2f1 + f2)/h2 + hf '''(ξ)
r=2, N=3 (четыре узла): f ''(x0) = (2f0 - 5f1 + 4f2 - f3)/h2 + 11h2f (4)(ξ)/12
f ''(x1) = (f0 - 2f1 + f2)/h2 - h2f (4)(ξ)/12
f ''(x2) = (f0 - 2f1 + f3)/h2 - h2f (4)(ξ)/12
f ''(x3) = (-f0 + 4f1 - 5f2 + 2f3)/h2 + 11h2f (4)(ξ)/12
В приведенных формулах ξ есть некоторая точка (своя для каждой из формул) из интервала (x0, xN). Остаточные члены этих формул находятся с помощью формулы Тейлора. При этом предполагается, что на отрезке [x0, xN] у функции f(x) непрерывна производная, через которую выражается остаточный член. При четном N в среднем узле для четной производной порядок точности формулы на единицу больше, чем в остальных узлах. Поэтому рекомендуется по возможности использовать формулы численного дифференцирования с узлами, расположенными симметрично относительно той точки, в которой ищется производная.
Содержание отчета
7. Титульный лист в соответствии с СТП1.2-2005.
8. Цель работы
9. Задание
10. Выполненная практическая работа в соответствии с заданием
11. Ответы на контрольные вопросы
12. Вывод
Контрольные вопросы:
1. Запишите основные задачи численного дифференцирования.
2. Запишите формулы вычисления погрешности вычислений.
3. Запишите 1-ый интерполяционный многочлен Ньютона.
4. Запишите 2-ой интерполяционный многочлен Ньютона.
5. Запишите первую и вторую формулы Ньютона в узлах для вычисления производных на краях таблицы.
ПРАКТИЧЕСКАЯ РАБОТА №19
Тема: Исследование свойств функции для определения для определения эффективности планирования технического цикла эксплуатации электроснабжения на железнодорожном транспорте.
Цель работы: Закрепить и систематизировать знания по теме «Основные численные методы».
Задание: Дано приближенное число х и его абсолютная погрешность Δ. Найти относительную погрешность δ этого числа.
| 1. | 4. x = 2, 71Δ=0,07 | 4. | x = 17,4 Δ=0,07 |
| 2. | 4. x = 17,9Δ=0,1 | 5. | x = 547,78 Δ=0,03 |
| 3. | 8. x = 3,54 Δ=0,04 | 6. | x = 25,6 Δ=0,08 |
Задание: Дано приближенное число х и его относительная погрешность погрешность δ. Найти абсолютную погрешность Δ этого числа.
| 7. | 5. x = 25,6δ =0,31% | 10. | x = 3,54δ =0,26% |
| 8. | 5. x = 17,4δ =0,40% | 11. | x = 35 δ =0,05% |
| 9. | 9. x = 2,71 δ =0,26% | 12. | x = 42,221 δ =0,5% |
Задание: Выполнить действие со строгим учетом погрешностей:
| 13. | х = 25 ± 0,1 у =13± 0, 2, х + у =? | 16. | х =1, 428 ± 0,0001 у = 0,14 ± 0,001, х: у =? |
| 14. | х = 0,17 ± 0,001 у = 6, 2 ± 0,05, х × у =? | 17. | 6. 156, 25 ± 0,001,
7.  =?
|
| 15. | х = 0,17 ± 0,001 у = 6, 2 ± 0,05, х × у =? | 18. | 1,56 ± 0,003,
 =?
|
Задание: Используя метод Эйлера, найти значения функции у, определяемой дифференциальным при начальном условии у (0) = 1;
у / (0) = 0 шаг h = 0,1. Найти у1:
| 19. | 8. у  = ху + 2
| 22. | 9. у// =у/ +ху +1 |
| 20. | 10. у/ = х2 - у | 23. | 11. у// =уу / +х |
| 21. | у// = у/ + у +1 | 24. | 12. у / = 5х + у + 3 |
Задание: Функция задана таблицей. Запишите интерполяционный многочлен:
| 25. | i 0 1 2 x -1 0 1 y 2 -1 0 | 28. | i 0 1 2 x 2 3 4 y -1 0 7 |
| 26. | i 0 1 2 x -1 0 1 y 7 -1 5 | 29. | i 0 1 2 x 1 3 4 13. y 12 4 6 |
| 27. | i 0 1 2 x -1 0 1 y -3 -1 7 | 30. | i 0 1 2 x -1 0 1 14. y 8 1 -2 |
Пояснения к работе:
Необходимые формулы:
