Алгоритм решения дифференциального уравнения первого порядка

y' = f(x,y) с разделяющими переменными

1. Рассмотрим производную y' как отношение дифференциалов ,

2. Перенесем dx в правую часть и разделим уравнение на h(y):

3. Разделим обе части уравнения на h(y) ≠ 0

4. Запишем уравнение в форме:

5. Проинтегрируем дифференциальное уравнение: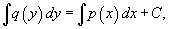

где C − постоянная интегрирования.

6. Вычислим интегралы, получаем выражение

 

Алгоритм решения дифференциального уравнения первого порядка

вида

1. Пусть y = uv, тогда по правилу дифференцирования произведения функций и линейное дифференциальное уравнения первого порядка примет вид  или

2. Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль:

3. Разделим в уравнении   переменные.

4.  Выполним почленное интегрирование, найдём функцию v. Так как функция v - решение уравнения, то её подстановка в уравнение  даёт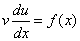

5. Найдём функцию u как общее решение этого уравнения.

6. Найдем решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций y = uv.

Содержание отчета

1. Титульный лист в соответствии с СТП1.2-2005.

2. Цель работы

3. Задание

4. Выполненная практическая работа в соответствии с заданием

5. Ответы на контрольные вопросы

6. Вывод

Контрольные вопросы:

1. Дайте определение дифференциального уравнения.

2. Дайте определение общего решения дифференциального уравнения.

3. Дайте определение дифференциального уравнения с разделяющими переменными.

4. Дайте определение дифференциального уравнения первого порядка.

5. Запишите формулу уравнение Бернулли.

ПРАКТИЧЕСКАЯ РАБОТА №7

Тема: Разложение функций в ряд Фурье.

Цель работы: Закрепить и систематизировать знания по теме: «Ряды».

Задание: Найдите первые четыре члена ряда по заданному члену:

1.		4.
2.		5.
3.		6.

Задание: Написать простейшую формулу n -го члена ряда по указанным его первым членам и записать ряд, используя знак суммы (S):

7.		10.
8.		11.
9.		12.

Задание: Исследовать ряд на сходимость, применяя признак Коши:

13.		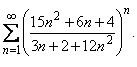16.
14.		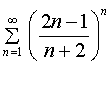17.
15.		18.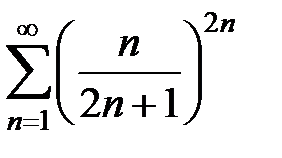

Задание: Исследовать ряд на сходимость, применяя признак Даламбера:

19.		22.
20.		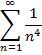23.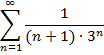
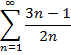
21.		24.

Задание: Разложите в ряд Фурье функцию:

25.		28.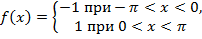
26.		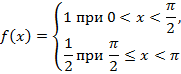29.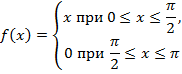
27.		30.

Пояснения к работе:

Необходимые формулы:

Частичная сумма ряда

Пусть 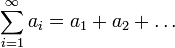— числовой ряд.

Число  называется n-ой частичной суммой ряда.

 

Сумма (числового) ряда — это предел частичных сумм, если он существует и конечен. Таким образом, если существует число   то в этом случае пишут  . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Признак Даламбера:

Если для ряда с положительными членами 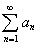существует  , то при p<1 ряд сходится, при p>1 ряд расходится, при p=1 вопрос о сходимости остается открытым.

Разложение в ряд Фурье периодических функций Т=2L,

Коэффициенты Фурье

;

;

 ; n = 1, 2, 3, …:;;, n = 1, 2, 3, …

Содержание отчета

1. Титульный лист в соответствии с СТП1.2-2005.

2. Цель работы

3. Задание

4. Выполненная практическая работа в соответствии с заданием

5. Ответы на контрольные вопросы

6. Вывод

Контрольные вопросы:

1. Дайте определение числового ряда.

2. Перечислите виды рядов.

3. Дайте определение понятию «сходящийся» и «расходящийся ряд.

4. Сформулируйте признак Даламбера.

5. Запишите общий вид тригонометрического ряда Фурье.

ПРАКТИЧЕСКАЯ РАБОТА №8

Тема: Расчет электрических цепей несинусоидальных электрических токов с применением рядов Фурье.

Цель работы: Закрепить и систематизировать знания по теме: «Ряды».

Форма выполнения задания: конспект

 

 

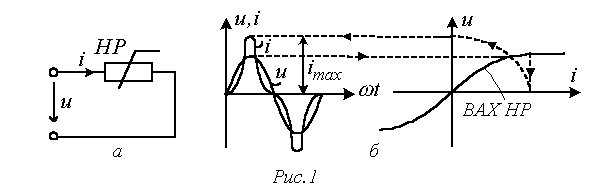
На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников. На практике к несинусоидальности напряжений и токов следует подходить двояко: в силовой электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи; поэтому здесь необходимо «всеми силами» поддержание синусоидальных режимов; в цепях автоматики и связи, где несинусоидальные токи и напряжения лежат в основе принципа действия электротехнических устройств, задача наоборот заключается в их усилении и передаче с наименьшими искажениями. В общем случае характер изменения величин может быть периодическим, почти периодическим и непериодическим. В данном разделе будут рассматриваться цепи только с периодическими переменными. Периодическими несинусоидальными величинами называются переменные, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены или несинусоидальностью источника питания или (и) наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами. В качестве примера на рис. 1,а представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (см. рис. 1,б).   Характеристики несинусоидальных величин Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока): Максимальное значение - . Действующее значение - . Среднее по модулю значение - . Среднее за период значение (постоянная составляющая) - . Коэффициент амплитуды (отношение максимального значения к действующему) - . Коэффициент формы (отношение действующего значения к среднему по модулю) - . Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) - . Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) - .   Разложение периодических несинусоидальных кривых в ряд Фурье Из математики известно, что всякая периодическая функция , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно. При разложении в ряд Фурье функция представляется следующим образом:   . 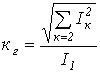(1)   Здесь - постоянная составляющая или нулевая гармоника; - первая (основная) гармоника, изменяющаяся с угловой частотой , где Т – период несинусоидальной периодической функции. 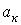В выражении (1) , где коэффициенты и 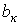определяются по формулам ; .