Титульный лист.
План работы оформляется с названием «Оглавление»; расположение – по центру.
Список библиографических источников оформляется под заголовком «Литература». Список литературы должен включать все использованные источники: сведения о книгах (монографиях, учебниках, пособиях, справочниках и т.д.) должны содержать: фамилию и инициалы автора, заглавие книги, место издания, издательство, год издания. При наличии трех и более авторов допускается указывать фамилию и инициалы только первого из них со словами «и др.». Наименование места издания надо приводить полностью в именительном падеже: допускается сокращение названия только двух городов: Москва (М.) и Санкт Петербург (СПб.). Приведенные библиографические источники должны быть отсортированы в алфавитном порядке по возрастанию. Список должен состоять не менее чем из трех источников.
Каждая новая часть работы, новая глава, новый параграф начинается с последующей страницы.
Приложение оформляются на отдельных листах, каждое приложение имеет порядковый номер и тематический заголовок. Надпись «Приложение» 1 (2.3...) оформляется в правом верхнем углу. Заголовок приложения оформляется как заголовок параграфа.
Объем работы не менее 10 листов напечатанных на компьютере (машинке) страниц; оглавление, список литературы и приложения не включаются в указанное количество страниц.
Текст рукописи печатается шрифтом № 14, с интервалом - 1,5.
Поля: слева - 3 см, справа - 1 см, сверху и снизу - 2 см.
Красная строка - 1,5 см. Межабзацный интервал – 1,8.
Название «Оглавление», «Введение», «Заключение», «Приложение», «Литература», а также заголовки глав и параграфов выделяются одинаковым темным, жирным шрифтом.
После цитаты в тексте работы используются знаки: «...», [1, С. 10], где номер библиографического источника берется из списка использованной литературы.
Обращение к тексту приложения оформляется следующим образом: (см. Приложение 1).
Оформление схем алгоритмов, таблиц и формул. Иллюстрации (графики, схемы, диаграммы) могут быть в основном тексте реферата и в разделе приложений. Все иллюстрации именуются рисунками. Все рисунки, таблицы и формулы нумеруются арабскими цифрами и имеют сквозную нумерацию в пределах приложения. Каждый рисунок должен иметь подпись.
Нумеровать страницы работы по книжному варианту: печатными цифрами, в нижнем правом углу страницы, начиная с текста «Введения» (с. 3). Работа нумеруется сквозно, до последней страницы.
В оглавлении указываются начальные страницы всех частей и параграфов работы (название главы отдельной страницы не имеет), кроме списка литературы и приложений (в тексте нумеруются).
Пишется слово «глава», главы нумеруются римскими цифрами, параграфы - арабскими, знак; не пишется; части работы «Введение». «Заключение», «Литература» нумерации не имеют.
Названия глав и параграфов пишутся с красной строки.
Заголовки «Введение», «Заключение», «Литература» пишутся посередине, вверху листа, без кавычек, точка не ставится.
Объем введения и заключения работы - 1,5-2 страницы печатного текста.
Работа должна быть прошита.
В работе используются три вида шрифта: 1 - для выделения названий глав, заголовков «Оглавление», «Литература», «Введение», «Заключение»; 2 - для выделения названий параграфов; 3 - для текстовки.
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
2. Цель работы
3. Задание
4. Выполненная практическая работа в соответствии с заданием
5. Ответы на контрольные вопросы
6. Вывод
Контрольные вопросы:
1. Дайте определение маршрута графа.
2. Дайте определение цикла графа
3. Сформулируйте понятие связности графа.
4. Дайте определение Эйлерова графа.
5. Дайте понятие дерева и перечислите его свойства.
ПРАКТИЧЕСКАЯ РАБОТА №12
Тема: Решение простейших комбинаторных задач и задач на определение вероятности с использованием теоремы сложения вероятности.
Цель работы: Закрепить и систематизировать знания по теме «Основы теории вероятности и математической статистики».
Задание: Решить задачу на использование классического определения вероятности:
| 1. | 2. Из букв слова «вероятность» наугад выбирается одна буква. Какова вероятность того, что выбранная буква будет: А-согласной; В – гласной; С – буква «о». | 4. | В урне 6 белых и 4 черных шаров. Из урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны вынимают еще один шар. Найти вероятность того, что этот шар тоже будет белым. |
| 2. | 2. Из урны, содержащей 10 белых шаров и 8 черных, вынимают подряд все находящиеся в ней шары. Найти вероятность того, что вторым по порядку будет вынут белый шар. | 5. | Бросаются две монеты. Какова вероятность, что обе монеты упадут «решкой» кверху. |
| 3. | 2. В первом ящике находятся шары с номерами от 1 до 5, а во втором от 6 до 10. Из каждого ящика вынули по одному шару. Найти вероятность следующих событий: 3. А- сумма номеров вынутых шаров не меньше 7; 4. В-сумма номеров вынутых шаров равна 11; 5. С-сумма номеров вынутых шаров не больше 11. 6. | 6. | Все натуральные числа от 1 до 30 написаны на одинаковых карточках и положены в урну. После тщательного перемешивания карточек из урны извлекается одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5? |
Задание: Решить задачу на использование классического определения вероятности:
| 7. | Игральная кость бросается один раз. Найти вероятность следующих событий: А- появление не менее 4 очков; В- появление не более 4 очков. | 10. | Брошены две игральные кости. Какова вероятность того, что абсолютная величина выпавших очков равна 2? |
| 8. | Игральная кость бросается два раза. Найти вероятность того, что оба раза появиться одинаковое число очков. | 11. | В лотерее 1000 билетов. Из них два билета выпадает выигрыш 200 рублей, на 4 билета -100 рублей, на десять – по 20 рублей, на тридцать – по 10 рублей, на пятьдесят - по 5 рублей, на двести – по 1 рублю, остальные билеты без выигрыша. Какова вероятность выигрыша по билету не менее 5 рублей? |
| 9. | Бросаются одновременно две игральные кости. Найти вероятности следующих событий: А- сумма выпавших очков равна 6. В- произведение выпавших очков равно 6. | 12. | Произвольным образом выбирается двузначное число. Какова вероятность того, что это число окажется: А-кратным 3; В- кратным 6; С- кратным 50. |
Задание: Решить задачу по теоремам сложения и умножения вероятностей:
| 13. | В ящике находятся пуговицы различных цветов белых– 50%; красных – 20%; зеленых – 20%; синих - 10%. Какова вероятность того, что взятая наугад пуговица окажется синего или зеленого цвета. | 16. | В магазин поступили телевизоры, 60% которых поставило предприятие, 25% -второе и 15% - третье. Какова вероятность того, что купленный телевизор изготовлен на первом и третьем предприятии. |
| 14. | Вероятность того, что стрелок, произведя выстрел выбивает 10 очков, равна 0,4; 9 очков -0,3 и, наконец 8 или меньше очков – 0,3. Найти вероятность того, что стрелок при одном выстреле выбьет не менее 9 очков. | 17. | Вероятность попадания в мишень для первого спортсмена 0,85, а для второго -0,8. Спортсмены независимо друг от друга сделали по одному выстрелу. Найти вероятность того, что в мишень попадет хотя бы один спортсмен. |
| 15. | При записи фамилий участников соревнований, общее число которых 420 оказалось, что начальной буквой фамилий у 10 из них была «А», у 6-«Е», у 9-«И», у 12-«О», у 5-«У», у 3-«Ю», у всех остальных фамилия начиналась с согласной. Определить вероятность, что фамилия участника начинается с гласной. | 18. | Из колоды в 36 карт наудачу вынимается одна. Какова вероятность того, что будет вынута пика или туз? |
Задание: Решить задачу по теоремам сложения и умножения вероятностей:
| 19. | Брошена игральная кость. Найти вероятность того, что выпадет четное или кратное трем число очков. | 22. | Консультационный пункт университета получает пакеты с контрольными работами из городов А, В, С. Вероятность получения пакета из города А равна 0,6, а из города В-0,1. Найти вероятность того, что очередной пакет будет получен из города С. |
| 20. | Найти вероятность того, что взятое наудачу двузначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно. | 23. | Из первого предприятия поступило 200 пробирок, из которых 190 стандартных, а со второго – 300, из которых 280 стандартных. Найти вероятность того, что взятая наугад пробирка будет стандартной. |
| 21. | В ящике имеются 30 шаров белого цвета и 5 черного. Из ящика наудачу берут один за другим 2 шара. Найти вероятность того, что оба шара окажутся черными. | 24. | В мастерской два мотора работают независимо друг от друга. Вероятность того, что в течение часа первый мотор не потребует внимания мастера, равна 0,9, для второго 0,85. Найти вероятность того, что в течение часа ни один из моторов не потребует внимания мастера. |
Задание: Решить задачу по теоремам сложения и умножения вероятностей:
| 25. | Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос? | 28. | Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго -0,8, для третьего – 0,9. Определить вероятность того, что все три стрелка попадут в цель. |
| 26. | Вероятность того, что в течение одного рабочего дня возникает неполадка в определенном медицинском приборе равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за 3 рабочих дня? | 29. | В урне 5 белых и 10 черных шаров. Из урны вынимается один шар, отмечается его цвет и шар возвращается в урну. После этого из урны берется еще один шар. Найти вероятность того, что оба вынутые шара будут белыми. |
| 27. | Вероятность того, что в летнюю сессию студент сдаст первый экзамен, равна 0,8; второй -0,9; третий – 0,8. Найти вероятность того, что он сдаст только первый экзамен. | 30. | В урне 3 белых и 6 черных шаров. Из урны вынимаются сразу два шара. Найти вероятность того, что эти шары будут разных цветов. |
Пояснения к работе:
Необходимые формулы:
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
2. Цель работы
3. Задание
4. Выполненная практическая работа в соответствии с заданием
5. Ответы на контрольные вопросы
6. Вывод
Контрольные вопросы:
1. Запишите определение вероятности.
2. Запишите свойства вероятности.
3. Запишите теорему сложения вероятностей.
4. Запишите теорему вероятности произведения двух зависимых событий.
5. Запишите формулу Байеса.
ПРАКТИЧЕСКАЯ РАБОТА №13
Тема: Решение задач на нахождение вероятности события при изучении и планировании рынка услуг на транспорте.
Цель работы: Закрепить и систематизировать знания по теме «Основы теории вероятности и математической статистики».
Задание: Заполните пропуск (выбор единственного ответа):
| 1. | Если случайные события А и В не могут появиться вместе, то они называются…
| 4. | Если появление события В не изменяет вероятность события А, то события А и В называются…
|
| 2. | Случайная величина, которая принимает конечное или бесконечное счетное множество значений, называется… 1. Непрерывной 2. Счетной 3. Дискретной 4. Бесконечной | 5. | Функция  называется
|
| 3. | Кривая, изображающая закон распределения для случайной переменной непрерывного типа, является графиком… 1. Вероятности 2. Плотности распределения 3. Функции распределения 4. Распределения | 6. | Если вероятность Р(А)=1, то событие называется… 1. Невозможным 2. Достоверным 3. Случайным 4. Независимым |
Задание: Решить задачу (выбор одного верного ответа):
| 7. | Бросили игральную кость. Какова вероятность, что выпадет четное число очков
Ответы:
| 10. | В группе 8 девушек и 6 юношей. Их разделили на две равные подгруппы. Сколько исходов благоприятствуют событию: 2 юноши окажутся в одной подгруппе, а 4 в другой? Ответы: а) 8 б) 168 в) 840 г) 56 |
| 8. | Монету подбросили 3 раза. Какова вероятность того, что “орел” выпадет 3 раза.
Ответы:
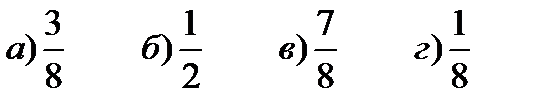
| 11. | Монету подбросили 3 раза. Какова вероятность того, что “орел” выпадет 1 раз.
Ответы: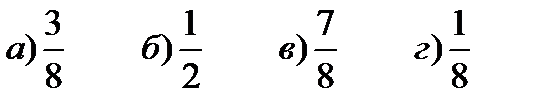
|
| 9. | В группе 8 девушек и 6 юношей. Их разделили на две равные подгруппы. Сколько исходов благоприятствуют событию: 3 юноши окажутся в одной подгруппе, а 3 в другой? Ответы: а) 8 б) 168 в) 840 г) 56 | 12. | Монету подбросили 3 раза. Какова вероятность того, что “орел” выпадет хотя бы 1 раз.
Ответы: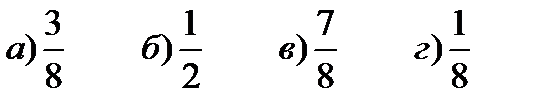
|
Задание: Запишите формулу (выбор одного верного ответа):
| 13. |  
Ответы: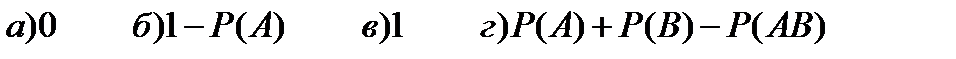 
|
| 14. | 
Ответы: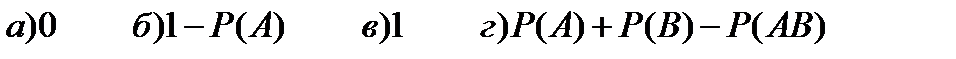
|
| 15. |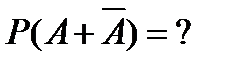 
Ответы: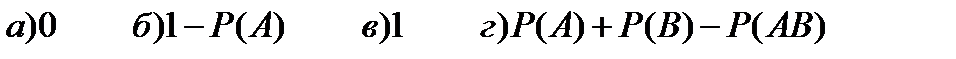
|
| 16. | Формула Байсса:
|
| 17. | Формула Бернулли:
|
| 18. | Формула полной вероятности:
|
Задание: Вычислить (выбор одного верного ответа):
| 19. | Найти Р (АВ), если 
Ответы: 
| 22. | Найти  , если Р(А) = 0,2
Ответы:
а) 0,5 б) 0,8 в) 0,2 г) 0,6
|
| 20. | Найти Р (АВ), если 
Ответы:
| 23. | Найти , если Р(А) = 0,8
Ответы:
а) 0,5 б) 0,8 в) 0,2 г) 0,6
|
| 21. | Найти Р (АВ), если 
Ответы:
| 24. | Найти , если Р(А) = 0,5
Ответы:
а) 0,5 б) 0,8 в) 0,2 г) 0,6
|
Задание: Вычислить (выбор одного верного ответа):
| 25. | События А и В несовместимы. Найти Р(А + В), если Р(А) = 0,7 Р(В)= 0,1 Ответы: а) 0,9 б) 0,8 в) 0,7 г) 0,6 | 28. | Найти Р (А+В), если Р(А)=0,5 Р(В)=0,2 Р(АВ)=0,1 Ответы: а) 0,5 б) 0,6 в) 0,9 г) 0,7 |
| 26. | События А и В несовместимы. Найти Р(А + В), если Р(А) = 0,25 Р(В)= 0,45 Ответы: а) 0,9 б) 0,8 в) 0,7 г) 0,6 | 29. | Найти Р (А+В), если Р(А)=0,2 Р(В)=0,8 Р(АВ)=0,1 Ответы: а) 0,5 б) 0,6 в) 0,9 г) 0,7 |
| 27. | События А и В несовместимы. Найти Р(А + В), если Р(А) = Р(В)= 0,3 Ответы: а) 0,9 б) 0,8 в) 0,7 г) 0,6 | 30. | Найти Р (А+В), если Р(А)=Р(В)=0,3 Р(АВ)=0,1 Ответы: а) 0,5 б) 0,6 в) 0,9 г) 0,7 |
Пояснения к работе:
