В статистики под понятием динамика подразумевают, изменение показателей общественно-экономических явлений во времени. Для изучения данных изменений строятся хронологические (временные) ряды, которые называются – рядами динамики.
Ряд динамики – последовательно расположенные в хронологическом порядке показатели, характеризующие развитие явления во времени.
Ряд динамики характеризуется двумя параметрами:
1. моментами времени (конкретными датами) или периодами (годы, кварталы, недели и т.д.), к которым относятся статистические данные.
2. непосредственно статистическими данными – уровнями динамического ряда (yi).
Ряды динамики можно подразделить в зависимости:
1. от вида приводимых в них статистических показателей -
· ряды динамики абсолютных величин,
· ряды динамики средних величин,
· ряды динамики относительных величин
Ряды абсолютных величин являются исходными, начальными, а ряды средних и относительных величин – производными.
2. от времени, отображаемому в динамическом ряде:
· моментные динамические ряды – уровни ряда выражают величину явления на определенный, конкретный момент времени (дату). Особенностью моментных рядов, является то, что суммировать их уровни не имеет смысла, так как суммирование будет включать одну и ту же величину несколько раз. В отличии от суммирования моментных уровней их разность имеет некоторый смысл,
· интервальные динамические ряды – уровни ряда отражают размеры изучаемого явления, за какой то промежуток времени (интервал). В отличии от моментных уровней, имеет смысл рассматривать суммы уровней следующих друг за другом, так как это будет являться итогом за более продолжительный период времени.
3. по полноте времени отображаемого в рядах динамики:
· полные ряды – их даты или периоды следуют друг за другом с равным интервалом,
· неполные ряды - их даты или периоды не следуют друг за другом с равным интервалом.
При построении рядов динамики необходимо соблюдать основное правило – правило сопоставимости уровней динамического ряда. Рассмотрим основные причины несопоставимости уровней динамического ряда.
Уровни динамического ряда могут быть несопоставимы:
1. по изучаемой территории. Несопоставимость территории возникает из-за изменения, со временем, границ изучаемых территорий. Например, нельзя сравнивать уровень рождаемости в Российской Империи и в Российской Федерации.
2. по кругу охватываемых объектов. Данная несопоставимость возникает вследствие перехода ряда объектов из одного подчинения в другое. Например, переход предприятия из одной корпорации в другую.
3. по критическому моменту регистрации. Например, при изучении изменения численности скота необходимо для изменения уровня брать одну и ту же дату, так как летом численность скота, как правило, больше.
4. из-за различия единиц измерения. Возникает, как правило, из-за того, что многие явления измеряются в разных единицах измерения. Поэтому, например, динамический ряд мощности, построенный в кВт, не должен содержать уровни, выраженные лошадиными силами.
5. из за несравнимости денежной оценки. Стоимость единицы продукции в рублях в 1985году несопоставима со стоимостью той же единицы продукции в рублях в 2003году.
6. по методике их расчета возникает из-за того, что одни и те же статистические показатели можно определять по-разному, например, средний удой можно посчитать на 1 среднегодовую корову, а можно посчитать на одну корову на начала года.
7. из-за разного понимания единиц изучаемой совокупности, то есть, например, если изучаем прибыль малых предприятий, нужно четко определить понятие малого предприятия.
При изучении явления во времени в статистики рассчитывают ряд показателей динамики, которые и будут характеризировать данное изменение. При этом анализу подвергаются уровни динамического ряда. Различают:
· начальный уровень (( ) или (
) или (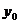 )), который показывает величину первого члена динамического ряда,
)), который показывает величину первого члена динамического ряда,
· конечный уровень ( ), который показывает величину конечного члена динамического ряда,
), который показывает величину конечного члена динамического ряда,
· средний уровень ряда  .
.
Статистический анализ динамических рядов основан на сравнении уровней динамического ряда. При этом сравниваемый уровень ряда динамики называется текущим уровнем, а уровень по отношению к которому проводится сравнение – базисным уровнем. В свою очередь базисным уровнем может быть:
· начальный уровень динамического ряда (либо любой другой, постоянно взятый за основу сравнения уровень). При сравнении с данным базисным уровнем текущего уровня получают базисные показатели динамики.
· уровень предыдущий текущему уровню. При сравнении с данным базисным уровнем текущего уровня получают цепные показатели динамики
· иногда за базу сравнения принимают средний уровень.
Показатели динамики
Абсолютный прирост  или
или  рассчитывается как разность двух уровней динамического ряда, один из которых принят за базу сравнения.
рассчитывается как разность двух уровней динамического ряда, один из которых принят за базу сравнения.
Цепной абсолютный прирост рассчитывается по формуле
 (6.1)
(6.1)
Базисный абсолютный прирост
 (6.2)
(6.2)
1. если динамический ряд обозначить как:  то,
то,
· цепной абсолютный прирост рассчитывается как
· 



· Цепной абсолютный прирост называют скоростью роста.
· базисный абсолютный прирост рассчитывается как
· 



2. если динамический ряд обозначить как:  то,
то,
· цепной абсолютный прирост рассчитывается как
· 



· базисный абсолютный прирост рассчитывается как
· 



Абсолютные приросты могут быть как положительные, так и отрицательные.
Коэффициент роста  – отношение текущего уровня ряда динамики к уровню принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в %
– отношение текущего уровня ряда динамики к уровню принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в %  . Коэффициент роста показывает во сколько раз уровень текущего периода выше или ниже уровня базисного периода, темп роста – сколько процентов он составил по отношению к базисному уровню.
. Коэффициент роста показывает во сколько раз уровень текущего периода выше или ниже уровня базисного периода, темп роста – сколько процентов он составил по отношению к базисному уровню.
1. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент роста рассчитывается как
·  (6.3)
(6.3)
· 



· базисный коэффициент роста рассчитывается как
·  (6.4)
(6.4)
· 



· последняя формула показывает коэффициент роста за весь период.
2. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент роста рассчитывается как
· 



· базисный коэффициент роста рассчитывается как
· 



последняя формула показывает коэффициент роста за весь период.
Коэффициент (темп) роста всегда число положительное.
Коэффициент (темп) прироста  показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%), то есть, сколько частей (процентов) составляет относительный прирост данного уровня по отношению к базисному уровню. Рассчитывается двумя способами:
показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%), то есть, сколько частей (процентов) составляет относительный прирост данного уровня по отношению к базисному уровню. Рассчитывается двумя способами:
Первый способ - как отношение абсолютного прироста к базисному уровню.
1. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент прироста рассчитывается как
·  (6.5)
(6.5)
· 



· базисный коэффициент прироста рассчитывается как
·  (6.6)
(6.6)
· 


 последняя формула показывает коэффициент прироста за весь период
последняя формула показывает коэффициент прироста за весь период
2. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент прироста рассчитывается как
· 



· базисный коэффициент прироста рассчитывается как
· 



последняя формула показывает коэффициент прироста за весь период
Второй способ – коэффициент (темп) роста минус 1 (100).
 или
или  (6.8)
(6.8)
Коэффициент (темп) прироста может быть как положительным, так и отрицательным.
Абсолютное значение одного процента прироста показывает часть абсолютного прироста, которая обеспечила 1% относительного прироста. Рассчитывается двумя способами.
Первый способ – как отношение абсолютного прироста к темпу прироста за тот же период
 (6.9)
(6.9)




Второй способ – как 0,01 часть от предыдущего (базисного) уровня.
 (6.10)
(6.10)
Для обобщения характеристики динамики, рассчитанной по уровням динамического ряда, определяют средние показатели динамического ряда. Средние показатели динамического ряда подразделяются на:
Средние уровни ряда.
В зависимости от вида временного ряда выбирают следующие методы расчета среднего уровня ряда:
Для интервального ряда динамики с равными интервалами средний уровень ряда 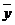 рассчитывается как средняя арифметическая простая исходных уровней
рассчитывается как средняя арифметическая простая исходных уровней
 (6.11)
(6.11)
где n – число уровней динамического ряда.
Для расчета среднего уровня моментного ряда динамики с равными отрезками между датами средний уровень определяют как среднюю хронологическую.

 (6.12)
(6.12)
где  – порядковый номер последнего уровня, если первый уровень динамического ряда обозначается как
– порядковый номер последнего уровня, если первый уровень динамического ряда обозначается как 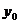
 (6.13)
(6.13)
Для интервального ряда динамики с неравными интервалами средний уровень ряда 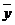 рассчитывается как средняя арифметическая взвешенная
рассчитывается как средняя арифметическая взвешенная
 (6.14)
(6.14)
где  - продолжительность периода между датами.
- продолжительность периода между датами.
С редние показатели изменения уровней ряда (средний абсолютный прирост, средние коэффициенты (темпы) роста и прироста)
Средний абсолютный прирост (средняя скорость роста)  определяется как средняя арифметическая из показателей абсолютного прироста.
определяется как средняя арифметическая из показателей абсолютного прироста.
 (6.15)
(6.15)
где  - количество абсолютных приростов.
- количество абсолютных приростов.
Средний коэффициент (темп) роста рассчитывается по формуле средней геометрической из индивидуальных коэффициентов (темпов) роста, так как необходимо учитывать, то обстоятельство, что скорость развития явления идет по правилам сложных процентов, где накапливается процент на процент.
если динамический ряд обозначить как: 
 (6.16)
(6.16)
где
 - знак произведения
- знак произведения
 – число коэффициентов роста.
– число коэффициентов роста.
Корни высоких степеней находятся логарифмированием, для чего прологарифмируем левую и правую части уравнения:
 (6.17)
(6.17)
Если использовать взаимосвязи, существующие между коэффициентами роста, вычисленными с переменной базой (цепные показатели), и коэффициентами роста, вычисленными с постоянной базой (базисные показатели), т.е. учитывая, что  , и динамический ряд обозначен:
, и динамический ряд обозначен:  - средний коэффициент роста можно определить по формуле:
- средний коэффициент роста можно определить по формуле:
 (6.18)
(6.18)
где  – число уровней динамического ряда.
– число уровней динамического ряда.
Средний коэффициент (темп) прироста рассчитать по индивидуальным коэффициентам (темпам) прироста, с помощью средней геометрической, нельзя, так как темпы прироста могут иметь отрицательные значения, а отрицательные числа логарифмов не имеют. Поэтому средний коэффициент (темп) прироста рассчитывают как:
 или
или 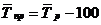 (6.19)
(6.19)






