Если динамический ряд составлен из уровней за короткие промежутки времени, то под влиянием множества факторов, которые действуют на уровни в разных направлениях, наблюдается колеблемость данных уровней в сторону повышения или снижения, из-за чего основная тенденция развития не просматривается.
Наиболее простым способом выявления основной тенденции развития является – метод укрупнения интервалов. Данный метод заключается в том, что первоначально полученный динамический ряд преобразуется в другой, уровни которого относятся к более продолжительным периодам времени. Например, ряд состоящий из уровней за месячный период, заменяется рядом с квартальными уровнями, ряд годовых уровней заменяется на пятилетия, и т.д. Новый динамический ряд образуется либо суммированием абсолютных величин первоначальных уровней, либо путем расчета средних уровней в объединенном периоде времени. При этом отклонения в уровнях укрупненного динамического ряда сглаживаются (взаимопогашаются) и более четко проявляется основная тенденция развития явления.
Другим методом механического выравнивания динамического ряда является метод скользящей средней. Данный метод заключается в замене исходного динамического ряда новым, расчетным рядом состоящим из средних уровней, за определенный период, со сдвигом на одну дату. Если исходный динамический ряд обозначить как: 
, то выроненный методом скользящей средней будет выглядеть как:
1. за трехлетний период
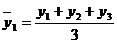
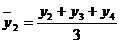
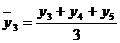
и т.д. (6.24)
2. за пятилетний период
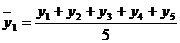
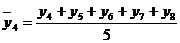и т.д. (6.25)
Выбор временного периода сглаживания, как правило, выбирается производно, в основном зависит от числа уровней в исходном динамическом ряду, так как новый динамический ряд сократится на 
уровней, где 
– число членов скользящей средней. Например, если сглаживание проводится за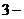 
летний период, то выровненный динамический ряд сократится на 
уровней, если за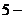 
летний период то на 
уровня.
Также, некоторую сложность, вызывает исследование динамического ряда, методом средних скользящих, состоящего из четного количества уровней. Если число членов средней скользящей обозначить как 
, то серединным будет уровень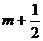 
члена ряда, т.е. наблюдается сдвиг периода, к которому относится серединный уровень. Так, например, при расчете скользящей средней для четырех уровней средняя для первого четырехлетия находится между вторым и третьем уровнями, для следующего четырехлетия между третьим и четвертым уровнями и т.д. Для того чтобы избежать данных сдвигов существует несколько методов. Наиболее часто применяемым, в силу своей простоты, является метод преобразования. При данном методе первый уровень первого интервала входит в сумму расчета средней только наполовину, затем берутся все остальные уровни первого интервала и половина первого уровня из следующего интервала. Например, для четырех летнего периода:
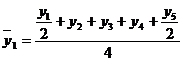
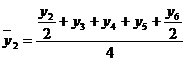
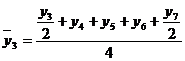и т.д. (6.26)
Методы механического выравнивания рядов динамики являются только первоначальными, предварительными, эмпирическими методами, которые подготавливают исходные данные для более сложных методов выражающих общую тенденцию развития.
