Аналитическое выравнивание позволяет определить основную тенденцию развития явления во времени. При этом уровни ряда динамики выражаются как функции времени:
 , (6.27)
, (6.27)
где  - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени
- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени 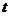 ,
,
 - отклонение от тенденции (случайное и циклическое)
- отклонение от тенденции (случайное и циклическое)
В итоге выравнивания динамического ряда получают обобщенный (суммарный), проявляющийся во времени результат действия всех факторов влияющих на развития изучаемого явления во времени.
При проведение аналитического выравнивания определяется зависимость  , при этом выбирается такая функция
, при этом выбирается такая функция  , чтобы она показывала содержательное объяснение изучаемого процесса. При аналитическом выравнивании, чаще всего применяют следующие трендовые модели:
, чтобы она показывала содержательное объяснение изучаемого процесса. При аналитическом выравнивании, чаще всего применяют следующие трендовые модели:
1. линейная  (6.28)
(6.28)
2. парабола второго порядка  (6.29)
(6.29)
3. кубическая парабола  (6.30)
(6.30)
4. показательная  (6.31)
(6.31)
5. экспоненциальная  (6.32)
(6.32)
6. модифицированная экспонента  (6.33)
(6.33)
7. кривая Гомперца  (6.34)
(6.34)
8. логистическая кривая 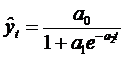 (6.35)
(6.35)
9. логарифмическая парабола  (6.36)
(6.36)
10. гиперболическая  (6.37)
(6.37)
Чаще всего выбор функции кривой проводится при помощи анализа графического изображения динамического ряда. Но по графику исходных уровней не всегда можно точно определить форму зависимости. Поэтому часто используют не исходный динамический ряд, а ряд механически сглаженных уровней, в котором случайные колебания гасятся в той или иной мере.
Кроме анализа графического изображения, для выбора формы кривой рассматривают ряд признаков:
1. если в исходном динамическом ряду наблюдаются более или менее постоянные разности первого порядка (абсолютные приросты), то есть не наблюдается тенденция к их увеличению или уменьшению выбирается линейная зависимость.
2. первые разности сами по себе имеют некоторую тенденцию развития, но вторые разности (абсолютные приросты абсолютных приростов) имеют примерно одну и ту же величину - применяют параболу второго порядка
3. если рост уровней исходного ряда идет по геометрической прогрессии, применяется показательная функция.
4. если первые разности имеют тенденцию к уменьшению с постоянным темпом – модифицированная экспонента.
5. если средние уровни, нанесенные на полулогарифмическую сетку, близки к прямой линии - простая экспонента.
6. если первые разности обратных значений средних уровней изменяются на один и тот же процент – логистическая кривая.
Оценку параметров уравнений  осуществляют при помощи:
осуществляют при помощи:
1. метода наименьших квадратов (МНК)
2. метода наименьших расстояний
3. метода избранных точек.
Чаще всего используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней динамического ряда от уровней выровненного динамического ряда.
Аналитическое выравнивание по прямой.
Аналитическое уравнение прямой имеет вид:
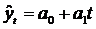 (6.38)
(6.38)
Для того чтобы рассчитать  найти неизвестные параметры уравнения
найти неизвестные параметры уравнения 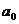 и
и  , для чего воспользуемся методом наименьших квадратов, который в данном случае даст систему из двух нормальных уравнений:
, для чего воспользуемся методом наименьших квадратов, который в данном случае даст систему из двух нормальных уравнений:
 (6.39)
(6.39)
Так как время понятие относительное и зависит только от точки отсчета, можно назначить такую точку отсчета, что сумма показателей времени исследуемого динамического ряда будет равна нулю(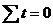 ).
).
При нечетном числе уровней изучаемого динамического ряда за точку отсчета принимают серединный уровень ряда, который обозначают как  . Периоды стоящие выше данного уровня обозначают отрицательными натуральными числами
. Периоды стоящие выше данного уровня обозначают отрицательными натуральными числами  и т.д. Уровни стоящие ниже
и т.д. Уровни стоящие ниже  обозначают положительными числами
обозначают положительными числами  и т.д. Например, ряд из 7 уровней будет обозначен как
и т.д. Например, ряд из 7 уровней будет обозначен как 
Если число уровней изучаемого динамического ряда четное, то точку отсчета берут между двумя серединами уровнями, она не обозначается. Периоды стоящие выше обозначают отрицательными натуральными числами  ; и т.д. Уровни стоящие ниже обозначают положительными числами
; и т.д. Уровни стоящие ниже обозначают положительными числами  ; и т.д. Например, ряд из 8 уровней будет обозначен как
; и т.д. Например, ряд из 8 уровней будет обозначен как  .
.
Подставив 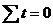 в уравнения системы, мы значительно ее упростим.
в уравнения системы, мы значительно ее упростим.
 (6.40)
(6.40)
отсюда
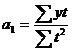 и
и  (6.41)
(6.41)
Для линейной зависимости параметр 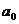 рассматривается как обобщенный начальный уровень ряда,
рассматривается как обобщенный начальный уровень ряда,  - как параметр силы связи, он показывает, на сколько единиц изменится результат при увеличении времени на единицу.
- как параметр силы связи, он показывает, на сколько единиц изменится результат при увеличении времени на единицу.
Подставив значение рассчитанных параметров уравнения 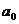 ,
,  и величину периодов времени
и величину периодов времени 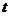 (
( – если ряд состоит из 7 уровней;
– если ряд состоит из 7 уровней;  – если ряд состоит из 8 уровней) рассчитаем выровненные теоретические значения уровней динамического ряда, которые образуют теоретическую прямую линию (линейный тренд). Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).
– если ряд состоит из 8 уровней) рассчитаем выровненные теоретические значения уровней динамического ряда, которые образуют теоретическую прямую линию (линейный тренд). Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).
Аналитическое выравнивание по параболе второго порядка.
Аналитическое уравнение параболы второго порядка имеет вид:
 (6.42)
(6.42)
Метод наименьших квадратов в данном случае даст систему из трех нормальных уравнений
 (6.43)
(6.43)
Используя метод приведения 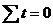 , и зная что и
, и зная что и  , упростим систему уравнений:
, упростим систему уравнений:
 (6.44)
(6.44)
Из данной системы легко определить 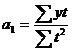 , а
, а 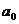 и
и  определяются решением системы двух уравнений с двумя неизвестными.
определяются решением системы двух уравнений с двумя неизвестными.
Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).
Аналитическое выравнивание по показательной функции.
Показательная функция аналитического выравнивания имеет вид:
 (6.45)
(6.45)
Для определения параметров уравнения также используют МНК, для чего предварительно логарифмируют уровни, и тогда логарифмы уровней отражаются линейной функцией:
 (6.46)
(6.46)
Примем 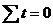 , тогда параметры уравнений
, тогда параметры уравнений  и
и  рассчитывают как:
рассчитывают как:
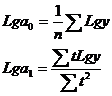 (6.47)
(6.47)
Рассчитав  и
и  определим
определим  , затем, потенцируя
, затем, потенцируя  находим
находим 
 .
.
Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).






