Показатели вариации для сгруппированных признаков

Общая дисперсия 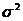  показывает величину вариации во всей совокупности, сложившуюся под влиянием всех факторов:

 – простая,                                                                                   (5.41)

 – взвешенная,                                                                          (5.42)

Внутригрупповая (случайная) дисперсия  показывает величину вариации внутри групп, на которые разбита совокупность, обусловленная случайными причинами:

 – простая,                                                                                       (5.43)

 – взвешенная,                                                                               (5.44)

где  – групповая средняя.

По всем группам рассчитывают среднюю внутригрупповую дисперсию :

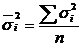 – простая,                                                                                               (5.45)

 – взвешенная,                                                                                      (5.46)

где  – общая численность по всем группам;

Межгрупповая (систематическая) дисперсия  показывает величину вариации групповых средних относительно общей средней, обусловлена систематическими причинами.

 – простая,                                                                                      (5.47)

 – взвешенная,                                                                           (5.48)

где  – число групп.

Все три вида дисперсии связанны Законом сложения дисперсий – общая дисперсия всегда равна сумме средней внутригрупповой и межгрупповой дисперсий:

,                                                                                                               (5.49)

 

Для характеристики влияния группировочного признака на общую вариацию рассчитывают корреляционное отношение :

,                                                                                                                     (5.50)

Чем больше корреляционное отношение, тем больше фактор, положенный в основание группировки, оказывает влияние на общую вариацию.

Пример 5.1. Имеются данные о количестве жителей  по районам проживания (табл. 5.1).

Таблица 5.1

№	тыс.человек.	№	тыс.человек.	№	тыс.человек.
1	2,0	5	3,0	9	5,5
2	2,5	6	4,0	10	6,0
3	2,5	7	5,5	11	6,5
4	3,0	8	5,5	12	7,0

 

Рассчитать.

1. Среднее количество человек в расчете на один район.

2. Моду.

3. Медиану.

4. Показатели вариации

· дисперсию;

· стандартное отклонение;

· коэффициент вариации.

Решение.

1. Так как значение варианты  в совокупности повторяется по несколько раз, с определенной частотой  для расчета среднего значения используем формулу среднюю арифметическую взвешенную:

2. Данный ряд является дискретным, поэтому модой будет варианта с наибольшей частотой – .

3. Данный ряд является четным, в этом случае медиану для дискретного ряда находят по формуле:

То есть, половина районов в исследуемой совокупности имеют численность до 4,75 тыс.чел. а половина свыше.

4. Для расчета показателей вариации составим таблицу 5.2, в которой рассчитаем отклонения , квадраты данных отклонений , расчет можно провести как по простым, так и по взвешенным формулам расчета (в примере используем простую):

 

 

Таблица 5.2

№
1	2,00	-2,42	5,84
2	2,50	-1,92	3,67
3	2,50	-1,92	3,67
4	3,00	-1,42	2,01
5	3,00	-1,42	2,01
6	4,00	-0,42	0,17
7	5,50	1,08	1,17
8	5,50	1,08	1,17
9	5,50	1,08	1,17
10	6,00	1,58	2,51
11	6,50	2,08	4,34
12	7,00	2,58	6,67
Итого	53,00	0,00	34,42
В среднем	4,4167

 

Рассчитаем дисперсию:

Рассчитаем стандартное отклонение:

Рассчитаем коэффициент вариации:ввв

 

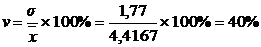
Пример 5.2. По предприятию представлены данные о заработной плате работников (табл. 5.3)

Рассчитать моду и медиану.

Решение.

Для интервального вариационного ряда мода рассчитывается по формуле:

где модальный интервал – интервал с наибольшей частотой, в нашем случае 3600-3800, с частотой

 - минимальная граница модального интервала (3600);

 - величина модального интервала (200);

 - частота интервала предшествующая модальному интервалу (25);

 - частота следующего за модальным интервалом (29);

 - частота модального интервала (68).

 

Таблица 5.3

Интервал по заработной плате, руб./чел.	Количество работников	Кумулятивная частота
3000-3200	15	15
3200-3400	17	32
3400-3600	25	57
3600-3800	68	125
3800-4000	29	154
Итого	154	-

 

Для интервального вариационного ряда медиана рассчитывается по формуле:

где медианный интервал это интервал, кумулятивная (накопленная) частота которого равна или превышает половину суммы частот, в нашем примере это 3600-3800.

 - минимальная граница медианного интервала (3600);

 - величина медианного интервала (200);

- сумма частот ряда (154);

 - сумма накопленных частот, всех интервалов, предшествующих медианному (57);

 – частота медианного интервала (125).

Пример 5.3. По трем хозяйствам одного района имеются сведения о цене одного и того же продукта: I – 1,29 руб., II – 1,32 руб., III – 1,27 руб. Необходимо рассчитать среднюю цену.

Решение. Так как цена обратный показатель, характеризующий покупательную способность денежной единицы используем формулу среднюю гармоническую простую.

Пример 5.4. Имеются данные о выручке от проданных конфет разных наименований, и о цене каждого вида конфет  (табл. 5.4).

 

Таблица 5.4

Наименование	Всего выручено	Цена
I	440000	24
II	380000	19
III	510000	21

Необходимо рассчитать среднюю цен.

Решение. Расчет средней цены по средней арифметической невозможен, так как отсутствуют сведения о проданных конфет , поэтому используем формулу средней гармонической взвешенной:

 

Пример 5.5. Имеются данные о средней прибыли на отдельных торговых точках и профессиональном разряде продавцов (табл. 5.5)  

Таблица 5.5

Разряд	Средняя прибыль тыс.руб.	Число точек.		Разряд	Средняя прибыль тыс.руб.	Число точек.
I	60	5		I	65	3
I	68	7		I	68	4
II	67	4		II	74	5
II	75	3		II	67	4
II	71	5		II	72	3
I	70	5		II	69	4

 

1. Рассчитаем общую дисперсию выборки (табл. 5.6):

Таблица 5.6

№	Средняя прибыль тыс.руб.	Число точек.
1	60	5	-8,67	75,17	375,84
2	68	7	-0,67	0,45	3,14
3	67	4	-1,67	2,79	11,16
4	75	3	6,33	40,07	120,21
5	71	5	2,33	5,43	27,14
6	70	5	1,33	1,77	8,84
7	65	3	-3,67	13,47	40,41
8	68	4	-0,67	0,45	1,80
9	74	5	5,33	28,41	142,04
10	67	4	-1,67	2,79	11,16
11	72	3	3,33	11,09	33,27
12	69	4	0,33	0,11	0,44
Итого		52			775,44
Среднее	68,67

 

 

2. Рассчитаем дисперсию для каждой группы:

а) Группа с разрядом – I (табл. 5.7)

Таблица 5.7

№	Средняя прибыль тыс.руб.	Число точек.
1	60	5	-6,38	40,70	203,52
2	68	7	1,62	2,62	18,37
3	70	5	3,62	13,10	65,52
4	65	3	-1,38	1,90	5,71
5	68	4	1,62	2,62	10,50
Итого		24			303,63
Среднее	66,38

б) Группа с разрядом равным II (табл. 5.8)

Таблица 5.8

№	Средняя прибыль тыс.руб.	Число точек.
1	67	4	-3,64	13,25	53,00
2	75	3	4,36	19,01	57,03
3	71	5	0,36	0,13	0,65
4	74	5	3,36	11,29	56,45
5	67	4	-3,64	13,25	53,00
6	72	3	1,36	1,85	5,55
7	69	4	-1,64	2,69	10,76
Итого		28			236,43
Среднее	70,64

3. Рассчитаем среднюю внутригрупповую дисперсию:

.

Проверим через правило сложения дисперсий:

4. Найдем межгрупповую дисперсию.

5. Рассчитаем корреляционное отношение:

.

То есть, фактор, положенный в основу группировки (разряд) оказывает среднее влияние на результат (среднюю прибыль).

6. Рассчитаем коэффициент детерминации

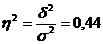
То есть вариация результативного признака на 44% обусловлена влиянием фактора – разряд продавца.