неполнотой контроля объекта, режимами контроля, методическими ошибками измерения. Влияние неполноты контроля на достоверность контроля можно продемонстрировать с помощью рисунка 3.1. Пусть контроль объекта проводится в моменты времени, определяемые пересечением кривой, характеризующей вероятность безотказной работы объекта с учётом только контролируемых параметров Pk, требуемого уровня Pтр безотказной работы объекта. В моменты времени проведения контроля, длительность которого предполагается равным нулю, вероятность безотказной работы объекта повышается до величины, определяемой вероятностью безотказной работы объекта, определяемой неконтролируемыми параметрами вектора состояния объекта. При этом предполагается, что значения остальных составляющих достоверности и начальное значение вероятности безотказной работы равны единицы. Как видно из рисунка интервалы между моментами проведения контроля со временем уменьшаются.

Рис. 3.1 Зависимости вероятностей безотказной работы объекта с учётом контролируемых Pк и неконтролируемых параметров Pн его состояния от времени t и влияние контроля на вероятность безотказной работы объекта.
Объём неконтролируемых параметров вектора состояния должен быть выбран таким образом, чтобы вероятность безотказной работы Pн, обусловленная ими не достигла требуемого уровня безотказной работы объекта Pтр в течении всего срока службы объекта.
На длительность интервала времени между проверками объекта, как видно из рисунка влияет объем неконтролируемых параметров, надежность объекта, требуемый уровень безотказной работы объекта Pтр, достоверность контроля.
Алгоритмическая достоверность контроля Da определяется старением получаемой информации за время контроля. С точки зрения повышения достоверности целесообразно сначала контролировать более устойчивые параметры с точки зрения надёжности. Наиболее целесообразно делать блоки одинаково надежными, тогда порядок выбора контролируемых параметров безразличен.
Избирательная достоверность контроля Dизб обуславливается соответствием выбранного управляющего воздействия по использованию объекта контроля идентифицированному классу его состояний. Снижение избирательной достоверности вызывается несоответствием числа возможных управляющих воздействий по использованию объекта контроля числу идентифицируемых классов его состояний приводит, что приводит к снижению эффективности использования объекта контроля.
Достоверность прогнозирования состояния объекта контроля Dп определяется качеством прогнозирования нахождения состояния объекта контроля в допустимой области на выбранном интервале времени.
Достоверность прогнозирования зависит от характеристик надёжности и допустимых областей параметров состояния объекта контроля, интервала времени и используемого метода прогнозирования. Задача оценки достоверности прогнозирования сводится к определению вероятности того, что многомерный случайный процесс, характеризующий вектор состояния объекта контроля, на выбранном интервале времени не выйдет за пределы поля допуска, находясь в начальный момент времени также в поле допуска
При обосновании достоверности прогноза наиболее часто используются два метода оценки достоверности. Первый метод основывается на том, что контролируемые параметры являются квазидетерминированными случайными процессами. Квазидетерминированными процессами называются такие процессы, случайные параметры, которых принимают конкретные неизвестные значения в начальный момент времени и в дальнейшем не изменяются, а изменение процессов во времени являются детерминированными. К таким процессам можно отнести различные полиномиальные функции, в частности, следующую функцию:

где ai случайные параметры с известными дисперсиями Dai и нулевыми математическими ожиданиями, t- время.
Для получения оценки достоверности прогнозирования необходимо информация о вероятностных характеристиках параметров квазидетерменированных случайных процессов.
Второй метод основан на том, что моделями параметров состояния являются случайные марковские процессы. В этом случае задача оценки достоверности прогнозирования решается на основе использования уравнения Фокера – Планка - Колмогорова или спектрально-марковского подхода. Учитывая, что показателями составляющих достоверности являются вероятности принятия правильных решений о состоянии объекта контроля с учётом соответствующих факторов и предполагая независимость этих компонент, общая достоверность канала «годен - негоден» будет определяться следующим образом.
 . (3.1)
. (3.1)
Достоверность контроля является основной характеристикой системы контроля, оценивающей качество получаемой информации. Поэтому при выборе количественной меры достоверности контроля, который может быть сделан различными способами, необходимо руководствоваться следующими соображениями. Достоверность контроля должна функционально зависеть от объема и точности измерения параметров, легко вычисляться и позволять достаточно просто решать обратную задачу - определять объем контроля и необходимую точность измерения параметров по заданной достоверности контроля. Поскольку качество решений при контроле оценивается вероятностями ошибок, то следует построить достоверность контроля как функцию вероятностей ошибок. Достоверность контроля можно определить в следующем виде:
 , (3.2)
, (3.2)
где  - безусловная вероятность ошибочных решений при контроле, равная при двуальтернативном контроле сумме безусловных рисков изготовителя и заказчика
- безусловная вероятность ошибочных решений при контроле, равная при двуальтернативном контроле сумме безусловных рисков изготовителя и заказчика
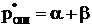 . (3.3)
. (3.3)
где a-безусловный риск изготовителя, определяемый совместной вероятностью принятия решения о том, что объект неработоспособен в то время когда он работоспособен, b-безусловный риск заказчика, определяемый совместной вероятностью принятия решения о том, что объект работоспособен в то время когда он неработоспособен. До проведения контроля безусловная вероятность ошибки равна априорному риску заказчика  , где P-вероятность безотказной работы объекта контроля. Поэтому априорная достоверность контроля равна вероятности попадания показателя качества или вектора состояния в свое поле допуска
, где P-вероятность безотказной работы объекта контроля. Поэтому априорная достоверность контроля равна вероятности попадания показателя качества или вектора состояния в свое поле допуска
 . (3.4)
. (3.4)
Эффект контроля заключается в том, что величина достоверности увеличивается от значения pдо величины  . Получим формулу для достоверности контроля, выраженную через вероятности правильных и ошибочных решений по параметрам, для объекта контроля, у которого параметры вектора состояния и погрешности их измерения являются взаимонезависимыми. При этом будем рассматривать случай неполного контроля. Пусть m - число контролируемых параметров, n - число параметров вектора состояния объекта, n- m - число неконтролируемых параметров. Достоверность контроля будем определять формулой (3.2). Запишем следующие формулы для определения безусловных рисков изготовителя и заказчика процесса контроля многомерного объекта с учетом контролируемых и неконтролируемых параметров
. Получим формулу для достоверности контроля, выраженную через вероятности правильных и ошибочных решений по параметрам, для объекта контроля, у которого параметры вектора состояния и погрешности их измерения являются взаимонезависимыми. При этом будем рассматривать случай неполного контроля. Пусть m - число контролируемых параметров, n - число параметров вектора состояния объекта, n- m - число неконтролируемых параметров. Достоверность контроля будем определять формулой (3.2). Запишем следующие формулы для определения безусловных рисков изготовителя и заказчика процесса контроля многомерного объекта с учетом контролируемых и неконтролируемых параметров
 , (3.5)
, (3.5)
 . (3.6)
. (3.6)
где ai, bi-безусловные риски соответственно изготовителя и заказчика при контроле – i-го параметра объекта, pi-вероятность безотказной работы объекта контроля по i-му параметру объекта, D0i-безусловная достоверность канала “годен” при проверке i-го параметра объекта, которая определяется совместной вероятностью принятия решения о работоспособности объекта контроля по i-му параметру в то время когда он является работоспособным.
Подставляя эти соотношения в формулу (3.2), получаем
 . (3.7)
. (3.7)
Полученное соотношение позволяет проанализировать зависимость достоверности контроля многопараметрического объекта от вероятностей правильных и ошибочных решений по параметрам и от полноты контроля. Если при измерении уменьшается априорная неопределенность, то достоверность контроля (3.7) является монотонно возрастающей функцией количества контролируемых параметров.
Формула для методической достоверности контроля следует из (3.7) при абсолютной точности измерения. Если истинные значения параметров находятся в пределах своих допусков и точность измерения абсолютная, то  ,
,  . Следовательно, методическая достоверность контроля равна
. Следовательно, методическая достоверность контроля равна
 . (3.8)
. (3.8)
Если количество контролируемых параметров равно нулю (m = 0), то методическая достоверность контроля равна
 . (3.9)
. (3.9)
Если контролируются все параметры, то методическая достоверность контроля равна единице. Это следует из общей формулы (3.7) и из формулы (3.8), если принять формально  . (3.10)
. (3.10)
В частном случае равенства вероятностей правильных и ошибочных решений для всех параметров формула (3.7) принимает вид,
 , (3.11)
, (3.11)
где  ,
, 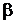 ,
,  - безусловные риски изготовителя и заказчика, и безусловная достоверность канала “годен” при контроле одного параметра объекта. Методическую достоверность контроля при одинаковых вероятностях правильных и ошибочных решений получим из (3.11) при
- безусловные риски изготовителя и заказчика, и безусловная достоверность канала “годен” при контроле одного параметра объекта. Методическую достоверность контроля при одинаковых вероятностях правильных и ошибочных решений получим из (3.11) при  =
= 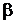 = 0,
= 0,  :
:
 . (3.12)
. (3.12)
При отсутствии контроля (m = 0) из (3.13) имеем  . При полном объеме контроля (m = n) из (3.12) получаем
. При полном объеме контроля (m = n) из (3.12) получаем  .
.
Для решения задач выбора необходимого объема контроля и потребной точности измерения параметров более удобно изменить шкалу отсчета достоверности контроля, положив, что до контроля достоверность равна нулю, а при абсолютно точном и полном контроле достоверность равна единице. Такая шкала изменения достоверности имеет место для относительной достоверности контроля, определяемой формулой:
 . (3.13)
. (3.13)
где pощ и pапр ош- соответственно апостериорная и априорная вероятности ошибок при принятии решений в процессе контроля.
До контроля апостериорная вероятность ошибочных решений равна априорной вероятности и достоверность контроля равна нулю. При абсолютно точном и полном контроле апостериорная вероятность ошибочных решений равна нулю, поэтому достоверность контроля равна единице.
Для решения задач синтеза основных характеристик контроля целесообразно построить такую зависимость достоверности контроля объекта от характеристик параметров, которая позволяла бы достаточно просто определять наиболее информативные параметры и назначать требуемую точность их измерения. С этой целью удобно использовать формулу для относительной достоверности контроля (3.13), заменив в ней априорную и апостериорную вероятности ошибочных решений соответствующими средне - квадратическими отклонениями
 , (3.14)
, (3.14)
где  -соответственно апостериорное и априорное средне- квадратическое отклонение скалярного показателя качества объекта.
-соответственно апостериорное и априорное средне- квадратическое отклонение скалярного показателя качества объекта.
Это соотношение достаточно точно отражает зависимость (3.13) вследствие того, что отношение средних квадратических отклонений мало, и практически следует рассматривать область вблизи нуля. В этой области формула очень хорошо аппроксимирует истинную зависимость достоверности контроля от отношения средних квадратических отклонений.
Достоверность контроля, определяемая формулой (3.14), нормирована и изменяется от нуля до единицы, поскольку апостериорная дисперсия изменяется от априорной дисперсии (нет контроля) до нуля (абсолютно точный и полный контроль).
К формуле достоверности контроля (3.14) можно прийти и с других позиций, если определить достоверность контроля в виде так называемой эффективности измерений
 , (3.15)
, (3.15)
где  - количество информации, получаемой при контроле, H - априорная энтропия показателя качества объекта,
- количество информации, получаемой при контроле, H - априорная энтропия показателя качества объекта,  - апостериорная энтропия показателя качества объекта. Априорная энтропия состояния объекта определяется формулой
- апостериорная энтропия показателя качества объекта. Априорная энтропия состояния объекта определяется формулой
 , (3.16)
, (3.16)
где  - плотность вероятности показателя качества объекта,
- плотность вероятности показателя качества объекта,  - интервал неопределенности, M - оператор математического ожидания. Апостериорная энтропия отличается от выражения (3.16) только заменой априорной плотности вероятности показателя качества соответствующей апостериорной плотностью вероятности.
- интервал неопределенности, M - оператор математического ожидания. Апостериорная энтропия отличается от выражения (3.16) только заменой априорной плотности вероятности показателя качества соответствующей апостериорной плотностью вероятности.
В случае нормального закона распределения показателя качества энтропии равны
 ,
,  . (3.17)
. (3.17)






