Алгоритмы, основанные на использовании сравнения отношения правдоподобия с пороговым значением, являются сложными и трудно реализуемыми.
Особенно затруднена в этом случае оценка качества процесса контроля, поскольку правило решения основано на сравнении сложной гипотезы со сложной альтернативой.
В связи с этим более широкое применение находят квазиоптимальные методы контроля, которые давно используются на практике.
Рассмотрим следующую постановку задачу. Пусть модель измерения определяется следующим соотношением (46).
Будем предполагать, что по результатам измерения Y получена оптимальная оценка 
-m-мерного вектора состояния X по критерию среднего квадрата ошибки оценки 
, где ошибка оценки 
. Рассмотрим двуальтернативный случай решения о состоянии объекта контроля. Пусть g0 и g1- соответственно непересекающиеся области допустимых и недопустимых значений вектора XÎW, W-m мерное пространство значений вектора X, при этом выполняются следующие условия: 
, 
. Идеальное решение о работоспособности объекта контроля zT=0 соответствует нахождению вектора XÎg0 в поле допуска, идеальное решение о неработоспособности объекта контроля zT=1 соответствует нахождению вектора XÎg1 вне поля допуска. Будем предполагать, что область допустимых значений g0 известна и представляет собой, как обычно бывает на практике, m-мерный параллелепипед с гранями, параллельными осям координат пространства W. Реальное решение о работоспособности объекта контроля z=0 соответствует нахождению вектора оценки ÎG0 в контрольном поле допуска G0, реальное решение о неработоспособности объекта контроля z=1 соответствует нахождению вектора оценки 
вне контрольного поля допуска G1, при этом выполняются следующие условия: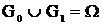 
, 
, 
, где W m-мерная область возможных значений X и . При этом форму и параметры допустимой области G0 требуется определить. Для упрощения алгоритма контроля будем использовать квазиоптимальный метод принятия решений, который заключается в сравнении компонент вектора оценки с допустимыми границами. В качестве формы допустимой области G0 целесообразно использовать такую же форму как у области допустимых значений вектора X g0, т.е. m-мерный параллелепипед c гранями параллельными осям координат пространства W. Таким образом, задача состоит в том, чтобы определить размеры параллелепипеда оптимальным способом 
. В качестве критерия оптимальности будем использовать критерии В.А. Котельникова и Неймана-Пирсона.
Запишем выражения для вероятностей ошибок двуальтернативного контроля.
Риск изготовителя, определяемый безусловной вероятностью появления в процессе контроля только ложных отказов
,
где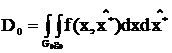 
- достоверность канала «годен»,определяемая совместной вероятностью нахождения вектора состояния объекта в поле допуска g0 и принятия решения системой контроля о том, что проверяемый объект работоспособен, 
- априорная вероятность попадания вектора X в область допустимых значений.
Риск заказчика, определяемый безусловной вероятностью появления в процессе контроля только необнаруженных отказов,
,
где 
- вероятность попадания вектора оценки состояния в область допустимых значений для оценки G0.
Достоверность D1 канала “негоден”, определяемая совместной вероятностью нахождения вектора состояния контроля в области недопустимых значений g1 и принятия решения системой контроля о том, что проверяемый объект неработоспособен
,
при этом выполняется условие нормировки
,
Чаще всего в процессе контроля контролируемые параметры выбираются независимыми друг от друга, так как при этом наименьшим количеством параметров можно обеспечить заданную полноту контроля и поиск неисправности происходит быстрее. В этом случае априорную плотность вероятности вектора состояния можно представить в следующем виде:
, (3.65)
где hi (xi-) плотность распределения i-го параметр вектора X.
Обычно при контроле выполняется условие, что погрешности измерения параметров также независимы друг от друга.
В этом случае плотности распределения 
и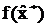 
также можно представить в виде произведений плотностей вероятности для отдельных компонент векторов параметров состояния Xi и оптимальных оценок 
, I=1,2,…,m
, 
. (3.66)
Будем считать, что эти условия выполняются. Тогда, можно записать следующие соотношения:
, (3.67)
, (3.68)
. (3.69)
где 
, 
,
.
Тогда выражения для рисков изготовителя и заказчика можно записать в следующем виде:
, (3.70)
. (3.71)
Кроме этих формул на практике часто используют следующие формулы:
, (3.72)
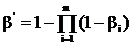, (3.73)
где 
- безусловная вероятность появления хотя бы одного риска изготовителя;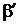 
- безусловная вероятность появления хотя бы одного риска изготовителя по одному из параметров.
При использовании указанных соотношений не выполняется условие нормировки
для 
,
При 
формулы, полученные выше для 
и 
и для 
и 
совпадают.
Задача оптимизации принимаемых решений в процессе контроля может быть определена следующим образом.
Необходимо определить оптимальные параметры допустимой области вектора по критериям Котельникова и Неймана-Пирсона, предполагая, что она принадлежит классу m-мерных параллелепипедов. При использовании области допустимых значений G0 в виде параллелепипеда обеспечивается независимость значений поля допуска для i-го параметра от значений j-го параметра, i,j=1,…,m, что значительно упрощает алгоритм контроля. Будем считать, что значение контрольного поля допуска G0i для i-го параметра определяется соотношением
G0i= AВi-ei -Aнi+ei =g0i+2ei, i=1,…,m, (3.74)
где поле контролируемое поле допуска g0i=AВi-Aнi, AВi, Aнi –соответственно верхнее и нижнее допустимые значения для i-го параметра, 2ei-неизвестное отклонение для i-го параметра контрольного поля допуска по отношению к контролируемому, при изменении которого определяется оптимальная область допустимых значений вектора .
,
где 
-m-мерная область оптимальных изменений области контрольных допусков по отношению к области g0.
Задачу оптимизации по критерию Котельникова математически можно сформулировать следующим образом:
. (3.75)
По критерию Котельникова параметры области G0 выбираем таким образом, при которых обеспечивается минимальное значение суммы безусловных вероятностей ошибок.
Задача оптимизации по критерию Неймана-Пирсона (прямой) определяется следующим соотношением:
(3.76)
Параметры области G0 выбираем таким образом, при которых обеспечивается минимальное значение риска изготовителя и при этом риск заказчика равен требуемой величине.
Задача оптимизации по инверсному критерию Неймана-Пирсона математически записывается следующим образом:
(77)
Таким образом, задача оптимизации сводится к нахождению значений 
, i=1,…,m, обеспечивающих единственный экстремум (безусловный или условный минимум). Наличие одного экстремума по переменным 
объясняется монотонностью изменения значений 
и 
при изменении ,i=1,…,m
На рисунках (3.4) и (3.5) представлены зависимости рисков изготовителя , заказчика и суммы ошибок 
от изменения .
При изменении ei от -¥ до (AВi-AНi)/2 значения риска изготовителя ai изменяется от 0 до значения вероятности нахождения i-го параметра Xi в поле допуска g0i P0i .
Рис.3.4 График зависимости риска изготовителя aI от изменения значений ei
При изменении ei от -¥ до (AВi-AНi)/2 значения риска заказчика bi изменяется от значения вероятности нахождения i-го параметра Xi вне поля допуска g1i P1i=1- P0i до 0..
Рис.3.5 График зависимости изменения риска заказчика bI и суммы ошибок ai +bI от изменения значений e
На рисунке 3.5 видно наличие минимума у зависимости суммы рисков изготовителя и заказчика от изменения значения ei.
С учётом соотношений (67)¸(69)) после простых преобразований решение задачи оптимизации алгоритма контроля по критерию Котельникова определяется следующими соотношениями:
, 
, 
. (3.78)
Решение системы уравнений позволяет найти оптимальные значения 
и затем оптимальную допустимую область G0· вектора контролируемых параметров
По критерию Неймана-Пирсона оптимальные значения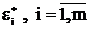 
определяются следующими соотношениями:
, 
. (3.79)
Если справедливы следующие условия, которые на практике чаще всего выполняются,
, 
, 
, 
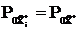, (3.80)
то уравнения для определения оптимальных значений 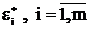могут быть записаны в следующем виде:
по критерию Котельникова:
, (3.81)
по критерию Неймана-Пирсона:
. (3.82)
Решая уравнения (77), (79) находим оптимальное значение 
, которое обычно нормировано стандартным значением погрешности измерения 
, i=1,…,m:
, (3.83)
где , i=1,…,m абсолютные значения одностороннего изменения i-го контрольного поля допуска G0i относительно контролируемого g0i.
Пусть выполняются условия (3.78). В этом случае характер изменения рисков изготовителя a и заказчика b от изменения числа параметров представлены на рисунках (3.6) и (3.7). На рисунке (3.6) представлены зависимости изменений вероятностей появления только рисков изготовителей a и только рисков заказчика b от количества контролируемых параметров, т.е.
Рис.3.6 График зависимостей рисков изготовителя и заказчика процесса контроля от изменения числа параметров состояния m
На рисунке (3.7) представлены зависимости изменений вероятностей появления хотя бы одного риска изготовителя a/ и хотя бы одного риска риска заказчика b/, определяемых в соответствии с соотношениями (3.72) и (73) от количества контролируемых параметров, т.е.
,
,
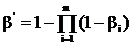Рис. 3.7 График зависимостей появления хотя бы одного риска изготовителя и хотя бы одного риска заказчика при контроле объекта от
числа параметров состояния m
Как видно из рисунка (3.6) зависимости a и b от изменения числа контролируемых параметров имеют максимумы, которым соответствуют следующие значения контролируемых параметров:
4. ТЕХНИЧЕСКАЯ ДИАГНОСТИКА
