Рассмотрим следующую линейную модель измерения, которая часто достаточно точно отражает процесс измерения сигналов в процессах контроля состояния объекта:
, (3.46)
где X- вектор состояния объекта размерности m´1, R - матрица измерения размерности N´m, H - вектор погрешностей измерений размерности N´1, Y- вектор результатов измерений размерности N´1. Рассматривается двуальтернативный случай контроля работоспособности объекта. В этом случае вектор состояния объекта контроля X может относиться либо к области допустимых значений g0 либо к области недопустимых значений g1. При этом выполняются следующие условия: 
Будем предполагать, что известны законы распределения векторов X и H. Поставим задачу определить байесово правило решение, которое обеспечит минимальный средний риск классификации сигналов X по результатам наблюдений Y.
С позиций теории статистических решений задача сводится к определению оптимального правила решения r·, которое минимизирует или обеспечивает нижнюю границу среднего риска R(r,h)
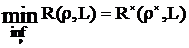, (3.47)
где h(x)-априорное распределение вектора X, 
-байесов риск, соответствующий оптимальному правилу решения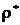 
. Оптимальное правило решения сводится к оптимальному разбиению пространства F значений векторов Y или пространства W оптимальных оценок 
вектора X на две области G0-допустимых значений и G1-недопустимых значений, обеспечивающих минимальное значение среднего риска. При этом должны выполняться следующие условия:
Оптимальное правило решения 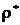определяет границу между G0 и G1.
С позиций теории статистических решений в данном случае целесообразно использовать оптимальный алгоритм, определяемый следующими соотношениями:
если 
< k принимается решение z = 0, (3.48)
если ³ k принимается решение z = 1, (3.49)
где отношение апостериорных вероятностей будет равно
,
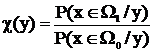k-порог, который определяется следующим соотношением
,
lij- функция потерь, соответствующая i-му истинному состоянию объекта контроля и j-м решению, принимаемом о состоянии объекта по результатам измерений Y, i, j= 0,1.
Вид порога определяет критерий оптимальности. Если положить
l10 = l01 = 1,
l00 = l11 = 0,
то в этом случае будет выбран критерий Котельникова (идеального наблюдателя). В этом случае минимизируется сумма двух ошибок - риска заказчика и риска изготовителя:
. (3.50)
Если положить l00 = l11 = 0, l01= 1, l10=1+l/p1, где неопределённый множитель Лагранжа l определяется условия заданного ограничения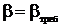 
, то получим критерий Неймана-Пирсона (β задано, α минимизируется)
(3.51)
Инверсный критерий Неймана-Пирсона (a задано, b минимизируется) определяется из следующего выражения:
. (3.52)
Основной недостаток оптимального метода решения рассматриваемой задачи заключается в сложности получаемых алгоритмов классификации состояний объекта контроля. Граница между областями G0 и G1 имеет очень сложный вид. Поэтому на практике часто используется квазиоптимальный способ оценки состояния объекта контроля.
Пример. Получим оптимальное правило контроля состояния объекта при нормальных законах распределения параметров состояния h(x) и погрешностей измерения f(y/x).
Будем предполагать, что контроль состояния объекта производится на интервале времени, в течении которого значения параметров объекта и погрешностей измерения H заметно не изменяются, т.е. X и H - векторы а не случайные векторные процессы.
Таким образом, априорная плотность распределения вектора состояния имеет следующий вид:
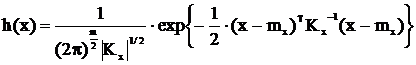, (3.53)
где математическое ожидание mx размерности m´1 и корреляционная матрица Kx размерности m´m вектора X известны и матрица Kx является невырожденной.
Условная плотность распределения f(y/x) вектора погрешностей измерения H является также нормальной и имеет следующий вид:
F(y/x)= 
, (3.54)
где корреляционная матрица KH размерности N´N вектора погрешностей измерения H известна и является невырожденной, математическое ожидание вектора H mH=0.
Тогда можно определить в следующем виде:
,(3.55)
где 
- оптимальная оценка вектора X по критерию минимума среднего квадрата ошибки оценки при получении вектора измерений Y;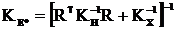 
- корреляционная матрица ошибок оптимальных несмещенных оценок вектора X.
В соотношение (3.55) входит плотность распределения
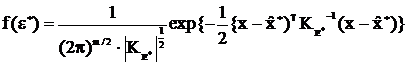, которую с учётом введения обозначения 
, где 
-ошибка оптимальной оценки вектора X, можно рассматривать как плотность вероятности оптимальной ошибки оценки:
. (3.56)
Отсюда следует, что отношение апостериорных вероятностей в данном случае определяется при фиксированном значении вектора y отношением вероятности попадания ошибки оценки в соответственно области 
и 
. Используя соотношения (3.48) и (3.49) определим алгоритм принятия решения процесса контроля.
Предположим, что все контролируемые параметры являются независимыми между собой и от погрешностей измерений, что часто выполняется на практике, так как контролируемые параметры выбираются таким образом, чтобы при данном объёме обеспечить максимальную информацию о состоянии объекта. Будем считать, что все погрешности измерений различных параметров также взаимонезависимы. Пусть mx=0, W0k=AВk-AНk, W1k=(¥¸AВk, AНk¸-¥), AВk=- AНk, где AВk-верхняя граница допуска на k-ый параметр, AНk-нижняя граница допуска на k-ый параметр)
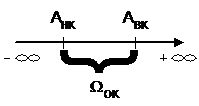
Рис.3.2 Поле допустимых и недопустимых значений k-го параметра состояния объекта
В этом случае отношение апостериорных вероятностей примет следующий вид:
.(3.57
Используем табличный интеграл ошибок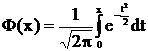 
. Тогда отношение апостериорных вероятностей можно представить в следующем виде:
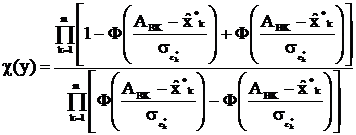(3.58)
Подставляя соотношение (3.58) в выражение (3.48) и (3.49), определим оптимальный алгоритм принятия решений о состоянии объекта контроля для исследуемой ситуации. При получении результата измерения y необходимо получить оптимальную оценку 
вектора x и затем вычислить отношение апостериорных вероятностей и сравнить с порогом k, значение которого определяется критерием оптимизации, в результате получим оптимальное решение при выборе класса состояний объекта контроля.
Рассмотрим частный случай, пусть m = 1, тогда
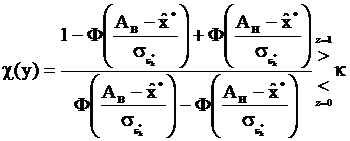. (3.59)
Выберем критерий Котельникова, которому соответствует значение порога 
= 1. В этом случае неравенство (3.59) можно привести к следующему виду:
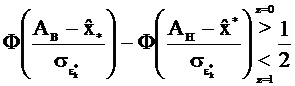. (3.60)
Алгоритм решения сводится к получению двух интегралов вероятности, нахождению их разности и сравнению с ½.
Исследуем данный алгоритм контроля однопараметрического объекта учитывая, что функция F обладает следующими свойствами:
- если аргумент равен нулю, то функция F равна нулю;
- если аргумент равен 
, то функция F равна единице;
- функция F нечетная;
-если аргумент равен 3, то функция F близка к единице.
Зависимости интегралов вероятности и их разности, определяемой левой частью неравенства (3.60), от изменения значений оптимальной оценки параметра X приведены на рисунке (3.3).
Рис.3.3 Зависимость разности двух интегралов вероятности от значений оптимальной оценки параметра состояния X
Как видно из рисунка границы допуска в общем случае не совпадают с значениями оценок , определяемых пересечениями зависимости разности двух интегралов вероятности с прямой, параллельной оси абсцисс и отстоящей от неё на расстоянии, определяемом значением ½. Таким образом, если перейти от оптимального алгоритма контроля к квазиоптимальному, определяемому сравнением значения оптимальной оценки с верхним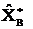 
и нижним 
значениями оценок, определяемых пересечением зависимостью разности двух интегралов вероятности со значением 1/2, то при принятии решения о состоянии объекта возникнет методическая ошибка. Величина этой ошибки будет тем меньше чем больше отношение 
поля допуска к среднеквадратическому значению ошибки оптимальной оценки. При часто выполняющихся значениях этого отношения 18 и больше (так как обычно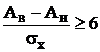 
, 
, где sx-среднеквадратическое значение параметра объекта) можно пренебречь влиянием методической ошибки на достоверность принимаемого решения. При этом контрольное поле допуска 
обычно незначительно превосходит контролируемое поле допуска g0=(AВ-AН). Полученный квазиоптимальный алгоритм контроля состояния объекта значительно проще оптимального алгоритма и сводится к сравнению полученной оптимальной оценки с верхнй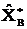 
и нижней границами контрольного поля допуска. При этом если значение оценки попадает в контрольное поле допуска принимается решение, объект работоспособен и в альтернативном случае – неработоспособен.
Если используется оптимальное правило решения
,
то вероятности ошибок контроля можно определить следующими выражениями:
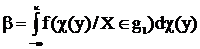, (3.61)
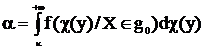, (3.62)
где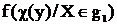 
и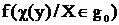 
плотности распределения отношения апостериорных вероятностей при условии соответственно, что вектор состояния объекта контроля X принадлежит области недопустимых значений g1 и области допустимых значений g0. Определение указанных плотностей распределения вызывает значительные трудности. В связи с чем при использовании оптимального правила решения вычисление вероятностей ошибок 
и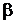 
и достоверности 
и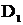 
каналов «годен» и «негоден» системы контроля является затруднительным.
При использовании же квазиоптимального правила решения о состоянии объекта контроля в случае использования областей допустимых значений g0 и G0 в виде m-мерных параллелепипедов не вызывает затруднений.
,
.
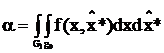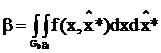Например, в случае однопараметрического объекта и для рассматриваемой линейной модели измерения выражения для безусловных рисков изготовителя и заказчика можно представить в следующем виде:
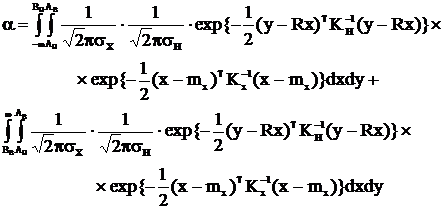, (3.63)
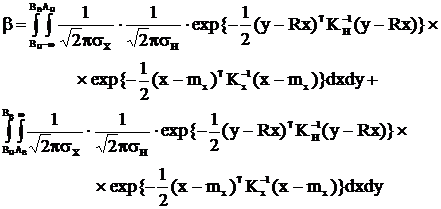. (3.64)
Для уменьшения ошибок контроля целесообразно:
1. уменьшить дисперсию ошибки оптимальной оценки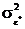 
путем использования более точных измерителей (уменьшить 
) и оптимальной фильтрации сигналов,
2. использовать комплексную обработку информации путём увеличения числа каналов и оптимальной обработки многомерных сигналов,
3. использовать измерители с некоррелированными погрешностями или измерители, у которых погрешности имеют отрицательный коэффициент корреляции
4.использовать оптимальные методы принятия решений о состоянии объекта контроля,
5. осуществить оптимальный выбор контрольных полей допусков при использовании квазиоптимального способа принятия решения о состоянии объекта контроля.
