Математические модели для дискретных систем описываются системой дифференциальных уравнений. При этом неизвестными в модели будут функции одной (обыкновенные дифференциальные уравнения) или нескольких переменных (уравнения в частных производных). Чаще всего в этих уравнениях в качестве независимой переменной выступает время, поэтому модели называются D -схемами. При помощи этих моделей описывается поведение электронных систем, систем автоматического управления.
При решении задач системотехники важное значение имеют проблемы управления большими системами.
Частными случаями динамических систем, описываемых D-схемами и выделенными в отдельный класс моделей (практическая специфика), являются системы автоматического управления (САУ).
Реальный объект предоставляется в виде двух систем: управляющей и управляемой.
Системы, для которых ошибки управления h ¢(t)=0 во все моменты времени, называются идеальными.
Задачей такой системы является изменение переменной y(t) согласно заданному закону с определенной точностью. При проектировании и эксплуатации такой системы необходимо выбрать такие параметры системы S, которые обеспечивали бы требуемую точность управления, устойчивость системы в переходном процессе.
Вид дифференциального уравнения, описывающего процессы в системе, позволяет говорить о свойствах системы.
 |
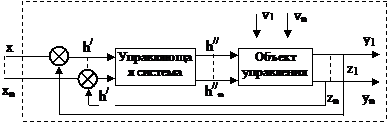– векторы входных и возмущающих воздействий (соответственно).
h ¢ (t) – вектор сигналов ошибки;
h ¢¢ (t) – вектор управляющих воздействий.
– векторы состояний системы и выходных переменных.
Обычно y(t)=z(t).
Пример. Рассмотрим одноканальную систему автоматического управления, описываемую с использованием D–схемы
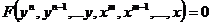, (3.5)
где 
– производные по t m и n -го порядков.
Пусть x0(t) и y0(t) – функции, характеризующие режим работы системы; D x(t), D y(t) – отклонения от x0(t) и y0(t), т.е.
x(t)= x0(t)+ D x(t) и y(t)= y0(t)+ D y(t).
Тогда уравнение (3.5) можно представить в виде (разложение в ряд Тейлора):
(6)
Так как полученное уравнение приближенно описывает рассматриваемый процесс, то производные вычисляют при некоторых фиксированных значениях входящих в него переменных, т.е. получается система с постоянными коэффициентами. Кроме того, уравнения получаются линейными относительно D x(t), D y(t) и их производных. Это весьма существенно, так как методы решения и исследования линейных систем значительно проще, чем систем общего вида, и более детально разработаны.
3.2. Дискретно–детерминированные модели (f-схемы)
Для формализации процессов функционирования систем используют математический аппарат теории автоматов. Это раздел теоретической кибернетики, в которой изучаются математические модели, автоматы. На основе этой теории система представляется в виде черного ящика, перерабатывающего входные сигналы в выходные, и имеющего свои внутренние состояния.
Конечный автомат – ящик, у которого множество внутренних состояний и входных сигналов, а соответственно множество и выходных сигналов, являются конечными.
Абстрактный конечный автомат – автомат, представляющий собой конечную математическую схему, характеризующуюся 6 элементами:
– конечным множеством входных сигналов X (входным алфавитом);
– конечным множеством внутренних состояний Z (внутренним алфавитом);
– конечным множеством выходных сигналов Y (выходным алфавитом);
– начальным состоянием z0, являющимся одним из состояний множества Z;
– функцией переходов j (z,x);
– функцией выходов Y (z,x).
Автомат функционирует в дискретном времени, которое представляется последовательностью тактов (интервалов времени, в течение которого состояние входных и выходных сигналов не изменяется).
Автомат, задаваемый F- схемой: F=<z, x, y, j, y, z0>,функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
В каждый момент времени F -автомат находится в определенном состоянии z(t). Это состояние определяется состоянием входного сигнала в этот момент времени. Поэтому выходной сигнал представляет собой функцию y(t)= y ((z(t), x(t)) от внутреннего состояния и входного сигнала в этот момент времени, а переход в следующее состояние будет определяться функцией переходов: z(t+1) = j [z(t), x(t)].
Работа конечного автомата происходит по схеме: в каждом t -м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1) -м такте, в новое состояние z(t+1) и выдачей некоторого выходного сигнала.
Любой автомат описывается системой уравнений:
. (7)
Для автомата I рода (автомат Мили) система выглядит следующим образом
Для автомата II рода (автомат Мура) состояние y(t) будет определено предыдущим состоянием входного сигнала. y(t)= y (z(t)) t=0,1,2… Выходные сигналы определяются внутренним состоянием системы на данном такте моделирования.
По числу состояний различают конечный автомат с памятью (1) и без памяти (2).
1. Конечные автоматы с памятью используются для моделирования последовательных схем (схем с памятью), которые имеют 2 и более состояний.
2. Конечные автоматы без памяти имеют одно состояние и используются для моделирования комбинационных схем, выходные состояния которых не зависят от внутреннего состояния системы, а только от входных сигналов y(t)= y (x(t)) t=0,1,2…
По характеру отсчета времени автоматы делятся на синхронные и асинхронные. В синхронных F -автоматах моменты времени, в которых происходит считывание входных сигналов, определяются принудительно синхронизирующим сигналом. После очередного синхронизирующего сигнала с учетом «считанного» и в соответствии с уравнениями (7) происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. То есть, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами.
Асинхронные автоматы считывают входной сигнал непрерывно, поэтому, реагируя на длинный входной сигнал, он может несколько раз изменять состояние на выходе пока не перейдет в устойчивое состояние, которое уже не может быть изменено этим входным сигналом.
Конечный автомат может быть задан каким-либо образом, если описать элементы множеств, которые входят в описание автомата F=<z,x,y, j, y,z0>. Необходимо выделить состояние z0.
В настоящее время используется 3 способа задания автоматов:
– табличный;
– графический;
– матричный.
