Приведенная стоимость оборудования

Определим теперь функцию зависимости затрат на оборудование от числа каналов. Отнеся затраты на оборудование к периоду морального устаревания оборудования (например, 5 лет), получим значение приведенных капиталь­ных затрат.

Пусть для организации АТС может быть закуплено оборудование разных типов, так что стоимость поддержания одного канала зависит от числа кана­лов сложным образом. Пусть простая АТС, обслуживающая до 10 каналов одновременно, вместе с затратами на поддержку каналов в течение 5 лет стоит 0.012 у. е. в пересчете на 1 минуту, если использовать все 10 каналов. но только 0.01 у. е, если использовать 1 канал. Более продвинутая АТС, об­служивающая до 50 каналов, стоит 0.05 у. е. (в пересчете на 1 минуту обслу­живания в течение 5 лет), но если использовать только 11 ее каналов, стоит 0.013 у. е. и т. п.

Учет затрат на оборудование и его обслуживание, зависящих нелинейным образом от числа каналов N, выполним с помощью табличной функции, ко­торая легко определяется в AnyLogic. Назовем функцию, дающую значение затрат на оборудование от числа каналов, приведенное к минуте времени. equipmentPrice. Зададим ее таблично. Для этого щелкните на кноп­ке или выберите команду Новая таблица преобразования в контекстном меню при выделенном корневом объекте модели Main. Назовите таблицу

equipmentPrice.

В появившемся окне свойств этого объекта в поле Данные определите функцию equipmentPrice согласно рис. 9.16. Щелкнув на кнопке График окна свойств таблицы, можно выбрать как закон интерполяции между за­данными таблично значениями, так и правила принятия решения, когда ар­гумент выходит за обозначенные пределы. Определите эти законы разумным образом, например простой линейной интерполяцией и экстраполяцией.

Расходы на оборудование при числе каналов n, приведенные к единице

Времени, Теперь МОЖНО ПОДСЧИТаТЬ ВЫЗОВОМ фуНКЦИИ equipmentPrice(N).

Целевая функция

Средний доход в нашей модели определяется случайной величиной gain, средний штраф определяется случайной величиной penalty, стоимость обо­рудования, уже приведенная к единице модельного времени, определяется функцией equipmentPrice (N). Для подсчета прибыли (в единицу времени) введите в модель переменную BenefitMean (среднюю прибыль), определяе­мую формулой так (рис. 9.17):

gain.mean() - penalty.mean() - equipmentPrice(N)

Здесь gain.meanO И penalty.mean () — математические ожидания величин

gain И penalty.

Запустите модель. Можно видеть, что прибыль в единицу времени (пере-менная BenefitMean) при установленных параметрах отрицательна. Измените

значение n, установив его 20. Прибыль стала положительной, порядка 0.35 у. е. в минуту. При числе каналов N, равном 100, прибыль становится меньше. Следовательно, существует оптимальное число каналов, обеспечи­вающее максимальную прибыль.

Для нахождения оптимального числа каналов, дающего максимальную при­быль, можно либо перебрать все значения N от 1 до, например, 100 в экспе­рименте для варьирования параметров, но можно и использовать экспери­мент с оптимизацией. Оптимизационный эксперимент в AnyLogic позволяет найти такие значения параметров модели, при которых обращается в мини­мум или максимум некоторая определенная пользователем целевая функ­ция. Значения целевой функции подсчитываются в AnyLogic каждый раз по окончании очередного выполнения модели, и алгоритм оптимизации авто­матически выбирает новые значения параметров для очередного запуска мо­дели. Оптимизация в AnyLogic реализована с использованием встроенного пакета OptQuest. Для оптимизации пользователь должен в соответствующих окнах задать функционал, который следует минимизировать либо максими­зировать, задать параметры и ограничения их диапазона, в которых должна выполняться оптимизация, а также указать ограничения, определяющие класс допустимых решений. Затем пользователь должен запустить оптими­зацию, и пакет OptQuest будет использовать метаэвристику рассеянного по­иска для выбора очередных значений входных параметров на основании значений целевой функции, полученных на предыдущих прогонах модели.

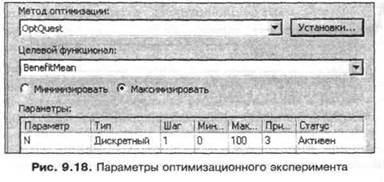
Щелкните по кнопке панели инструментов и в появившемся окне вы­берите Новый оптимизационный эксперимент. В окне свойств эксперимента установите BenefitMean в качестве целевого функционала из выпадающего меню. Изменяемым параметром является к (выберите его тоже из выпадаю­щего меню), верхнюю границу n установите 100, условие останова одного прогона — 10 000 единиц времени, число прогонов для нахождения опти­мального числа каналов сделайте 30 (открыв окно Установки OptQuest щелчком по кнопке Установки) и выберите задачу максимизации функцио­нала (рис. 9.18).

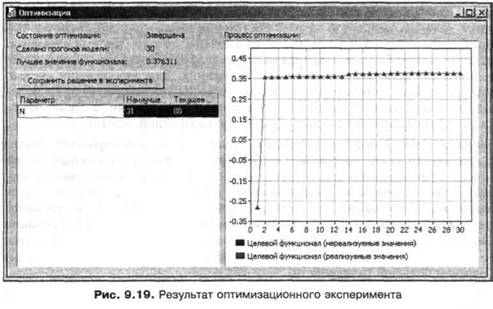
Сделайте этот эксперимент текущим, выбрав соответствующую команду в контекстном меню объекта (его название в этом случае будет изображаться жирным шрифтом). Запустите модель. Оптимизационный эксперимент найдет наилучшее число каналов 31, максимальная прибыль поставщика сервиса в этом случае будет 0.376 у. е. в минуту (см. рис. 9.19). Вы можете сравнить вашу модель с моделью ErlangProblem2 в папке Model Examples\Part III.

Заключение

AnyLogic включает несколько видов экспериментов, которые можно выпол­нять с разработанной имитационной моделью. Одним из самых важных с точки зрения практического применения является оптимизационный экспе­ римент.

Многие модели в бизнесе, науке и технике включают существенные нели­нейности, комбинаторные зависимости и неопределенности, которые легко представимы в имитационных моделях, но являются слишком сложными для представления формальным математическим аппаратом, наборами ма­тематических формул. Это препятствует непосредственному применению классических методов оптимизации в таких системах. Целью пакета OptQuest, встроенного в AnyLogic, как раз и является оптимизация систем, которые не могут быть представлены как математические модели и оптими­зация в которых не может быть выполнена с помощью классических алго­ритмов. В пакете реализованы современные мощные алгоритмы оптимиза-

ции (см. [LM03]). Пакет использует подход "черного ящика" для вычисления значений целевой функции: он устанавливает входные параметры и обраща­ется к имитационной модели, которая по набору входных параметров воз­вращает значение целевой функции.

Любой оптимизатор, используемый в системе имитационного моделирова­ния, должен иметь разумную эвристику для выбора очередного варианта исходных факторов системы в случае, когда система задана как "черный ящик" своими входными/выходными соотношениями. Выбор такой эври­стики является непростой задачей. В течение многих лет возможности оп­тимизации сложных систем были ограничены только теми проблемами, которые можно было формализовать с помощью аппарата линейного, нели­нейного или целочисленного программирования. Для оптимизации систем, которые не могли быть формализованы в рамках этих математических моде­лей, использовался метод случайного поиска с эвристиками, которые обыч­но разрабатывались специально для каждой конкретной задачи.

Недавние результаты исследований новых типов метаэвристик (scatter search, генетических алгоритмов и tabu search) сделали возможным разра­ботку систем оптимизации, которые могут организовать процесс поиска оп­тимального решения без формального представления системы в рамках математического программирования. Именно к этому классу систем отно­сится встроенный в AnyLogic пакет оптимизации OptQuest. Использование AnyLogic совместно с пакетом OptQuest в ряде производственных проектов по оптимизации принятия решений показали применимость этого подхода к задачам большой размерности.

Глава 10