Основные типы и профили каналов. Каналы в зависимости от их назначения, рода грунтов, применяемых механизмов, местных условий устраиваются различной формы поперечного сечения.
Основными формами поперечных сечений каналов являются: трапецеидальная, прямоугольная, треугольная, параболическая (рис. 13.1).
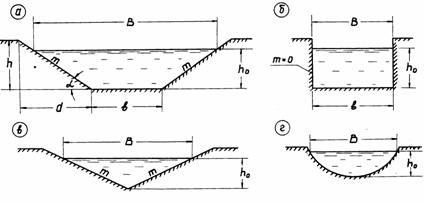
Рис. 13.1. Формы поперечных сечений каналов
Параболическая и трапецеидальная формы поперечных сечений применяется в каналах, прокладываемых в обычных грунтах.
Треугольная форма русла прокладывается в тех случаях, когда по каким-либо причинам имеются ограничения на местности.
Прямоугольная форма поперечного сечения русла устраивается в каналах, прокладываемых в горных породах, не требующих укрепление стенок русла от размыва и обрушения.
Гидравлические элементы поперечного сечения канала. Наибольшее распространение в строительной практике получили каналы трапецеидального сечения, характеризующейся коэффициентом откоса m, шириной канала по дну b и глубиной канала h (рис. 13.1,а).
Коэффициент откоса m представляет собой отношение заложения d к глубине канала h и выражается котангенсом угла наклона плоскости откоса к горизонту, т.е.
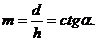 (13.1)
(13.1)
Его величина зависит от рода и качества грунта, в котором устроен канал, а также от принятого способа укрепления откоса.
Глубина и ширина канала по дну зависят от расчетной пропускной способности канала.
Приведем основные зависимости для определения характеристик каналов трапецеидального сечения, необходимых при выполнении гидравлических расчетов.
Площадь живого сечения
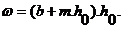 (13.2)
(13.2)
Ширина живого сечения поверху
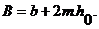 (13.3)
(13.3)
Смоченный периметр
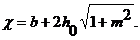 (13.4)
(13.4)
В этих формулах h 0 - глубина наполнения канала при равномерном движении воды в нем.
Гидравлический радиус
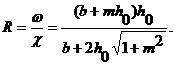 (13.5)
(13.5)
Прямоугольная, треугольная формы сечения канала представляют собой частный случай трапецеидального сечения. В первом случае m = 0, во втором случае b = 0, соответственно преобразуются и расчетные зависимости (13.2) - (13.5).
Основные формулы для расчета равномерное движение жидкости в открытых руслах. При равномерном движении жидкости глубина потока по его длине остается неизменной величиной. Эта глубина называется нормальной глубиной и обозначается через h 0.
Пьезометрическая линия в открытых потоках (каналах) совпадает со свободной поверхностью и, следовательно, при равномерном движении она параллельна дну потока. Поэтому гидравлический и пьезометрический уклоны равны уклону дна канала i.
Основной расчетной формулой при расчете каналов является формула Шези
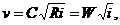 (13.6)
(13.6)
где v - средняя скорость движения потока; W определяется как скоростная характеристика (модуль скорости), имеет размерность скорости,
 , (13.7)
, (13.7)
R - гидравлический радиус; С - коэффициент (коэффициент Шези).
Коэффициент Шези, как отмечалось ранее, определяется по формуле Н.Н.Павловского
 ; (13.8)
; (13.8)
Здесь n - коэффициент шероховатости стенок русла (определяется по справочнику в зависимости от состояния русла); y - показатель степени, зависящий от коэффициента шероховатости русла n и гидравлического радиуса R, 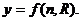 По формуле академика Павловского (при
По формуле академика Павловского (при 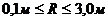 )
) 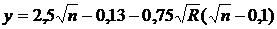 . При n =0,011
. При n =0,011 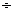 0,020 можно принимать
0,020 можно принимать  . Тогда для определения коэффициент Шези применяется формула Маннинга
. Тогда для определения коэффициент Шези применяется формула Маннинга
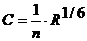 -. (13.9)
-. (13.9)
Для практических расчетов с достаточной степенью точности при R < 1,0м можно принять  , а при R > 1,0м
, а при R > 1,0м 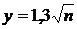 .
.
Применительно к расходу формула Шези имеет вид
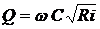 . (13.10)
. (13.10)
Обозначив 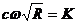 , (13.11)
, (13.11)
получим формулу для расчета расхода в следующем виде
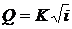 , (13.12)
, (13.12)
где К - модуль расхода (расходная характеристика). При i =1 К = Q, т. е. модуль расхода равен такому расходу, который установится в канале при заданной глубине и уклоне дна канала, равном единице (канал проложен под углом в 45°)






