Задача 1. Определение расхода Q, пропускаемого каналом.
Задание: Определить расход Q, пропускаемый каналом, если известны глубина наполнения канала ho,ширина канала по дну b,уклон дна I 0 и род грунта, в котором устроен канал (или характер его облицовки, если предполагается укрепление дна и стенок канала, т. е. известен коэффициент шероховатости n).
Решение: В зависимости от рода грунта или характера облицовки по справочным данным (например в учебнике) определяется коэффициент откоса m и коэффициент шероховатости n, вычисляются величины ωи R.. Величина коэффициента С определяется для найденных значений R и n по формуле Н.Н.Павловского (13.8) (по этой формуле составлены таблицы) или по формуле Маннинга (13.9). Определив таким путем все величины, входящие в уравнение равномерного движения значение искомого расхода вычисляют непосредственно по уравнению
Задача 2. Определение уклона дна канала I 0.
Задание: Определить уклон дна канала I 0, который необходим для пропуска заданного расхода Q при известных размерах канала (b и m) и роде грунта или одежды.
Решение: Непосредственно из уравнения равномерного движения имеем 
где в соответствии с формулой (13.1) модуль расхода (расходная характеристика) K 2 = C 2 w 2 R. Значения величин С, w и R определяются так же, как и в задаче 1.
Задача 3, а. Определение глубины наполнения канала h 0.
Задание: Определить глубину наполнения канала h 0, при которой канал шириной по дну b, с уклоном I 0, коэффициентом откоса m и шероховатости n пропустит расчетный расход Q.
Решение: Непосредственно по уравнению равномерного движения глубина наполнения h 0вычислена быть не может, так она входит в параметры уравнения С, w, c, R в довольно сложном виде. Поэтому задачу решаем методом подбора. Преобразуем уравнение (13.10) с учетом выражения (13.11) для модуля расхода К к следующему виду 
откуда 
Анализ последнего уравнения показывает, что параметры его, стоящие в левой части не зависят от глубины наполнения канала, в то время как правая часть (расходная характеристика) в силу равенства (13.11) является функцией глубины наполнения, т.е. К = К (h 0).
Это положение дает возможность определить глубину наполнения канала графоаналитическим способом. Сущность его заключается в следующем. Задаемся рядом произвольных значений h и по приведенным выше формулам при каждом значении h определяем величины 
. Затем по формуле Шези определяем расход Q при данной глубине h. После чего строим график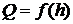 
(рис. 13.2,а).
Рис. 13.2. Графики зависимости расхода Q от глубины h и ширины канала b
Отложив на оси абсцисс точку, соответствующую заданному расходу Q, найдем по графику искомую глубину h.
Задача 3, б. Определение ширины канала.
Задание: Определить ширину канала по дну b, необходимую для пропуска заданного расхода при известных значениях h 0, Q, m, I 0, n.
Решение: Задача решается так же методом подбора. Задаваясь различными значениями b, последовательно определяем величину и по формуле Шези вычисляем расход Q, после чего строим график 
(рис. 11.2,б). На графике по заданному расходу Q зад найдем искомую величину ширины канала понизу b иск. Как видно на рис. 13.2,б кривая выходит не из начала координат. Отрезок 0 B характеризует расход в треугольном русле при b = 0.
Определение глубины потока в канале с помощью гидравлического показателя русла. Установлено, что отношение модулей расходов в квадрате, равно отношению соответствующих им глубин в некоторой степени х:
(13.13)
(13.14)
Величина степени х в среднем остается постоянной для данной формы русла и потому называется гидравлическим показателем русла. Так, для широкого прямоугольного русла х =3, для параболического (второго порядка) х =4, для треугольного х =5.
Зададимся двумя произвольно выбранными глубинами h 1 и h 2 и определим при этих глубинах расходные характеристики K 1 и K 2. Используя формулу (11.14) составим расчетное уравнение, применяя формулу (13.13)
,
где h 0 - искомая глубина потока в канале; K 0 - соответствующий этой глубине модуль расхода (расходная характеристика), 
I - заданный уклон дна канала; h 1 - произвольное взятая глубина; 
- соответствующий этой глубине модуль расхода; 
- соответственно площадь живого сечения потока, коэффициент Шези и гидравлический радиус при глубине h 1. Преобразуем расчетное уравнение к виду 
откуда искомая глубина 
.
Этот способ решения представляется менее трудоемким по сравнению с графическим способом (методом подбора).
Гидравлически наивыгоднейшее сечение канала. Гидравлически наивыгоднейшем сечением канала называется такое, у которого при заданной площади живого сечения ω, шероховатости n, крутизне заложения откосов m и продольном уклоне i пропуская способность наибольшая (Q max).
При одной и той же площади живого сечения соотношения между шириной канала понизу и глубиной могут быть самые разнообразные. У всех сечений, изображенных на рис. 11.3, площади живых сечений одинаковы, а пропускная способность разная.
Рис. 13.3. Поперечные сечения каналов с глубиной наполнения h1, h2, h3
Определим гидравлически наивыгоднейшее сечение канала.
Пропускная способность канала. Как определено ранее, определяется по формуле Шези 
По условиям задачи ω- задано; I – задано; 
.
Следовательно, Q max будет при R max.
Гидравлический радиус 
т. к. ω заданно, то R maxбудет при cmin. Величинаcmin будет наблюдаться при 
Определим значения соответствующих величин:
,
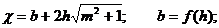
отсюда
, 
Подставив соответствующие значения величин, получим:
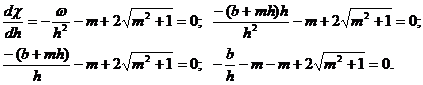
Отсюда соотношение ширины канала понизу и глубины, соответствующие гидравлические наивыгоднейшему сечению канала будет составлять
Для прямоугольных русел 
и 
.
Расчет каналов на размыв и заиление. В проектируемом канале значение средней скорости, вычисленной по формуле (13.6), должно находится в определенных пределах д опустимых скоростей потока в канале, устанавливаемых в соответствии с неравенством
(13.15)
где: v max – максимальная допустимая (допускаемая) средняя скорость течения воды в канале, которую называют неразмывающей скоростью; v min - минимальная допустимая средняя скорость течения воды в канале при равномерном движении, иначе называемая незаиляющей скоростью.
Если средняя скорость движения воды в канале будет больше максимальной допускаемой скорости для данного грунта или типа облицовки канала (т.е. при v > v max) произойдет размыв и разрушение канала. Во избежание этого сечение канала должно быть увеличено, усилено креплением его откосов и дна или уменьшен уклон дна I 0. Значения максимальных допускаемых (неразмывающих) скоростей приводятся в справочниках.
Если вода, поступающая в канал, содержит взвешенные наносы, средняя скорость потока воды в канале должна быть несколько больше (или в пределе равна) той минимальной скорости, при которой не происходит осаждения этих наносов. Если окажется, что v < v min, под влиянием выпадения и осаждения наносов канал будет заиливаться, что потребует его постоянных расчисток. Величина минимально допустимой (незаиляющей) скорости также приводятся в справочниках.
5.2. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ
5.2.1. ОСНОВНЫЕ ПАРАМЕТРЫ НЕРАВНОМЕРНОГО ДВИЖЕНИЯ
