Критическое, спокойное и бурное состояние потока

 

При постоянном расходе Q глубина потока h может быть различной, в зависимости от уклона дна I_o, шероховатости n.

Учитывая, что площадь живого сечения при заданной форме и размерах поперечного сечения русла однозначно определяется глубиной h: w = f(h), замечаем, что при постоянном расходе удельная энергия сечения потока является функцией только глубины h. Нарисуем график этой функции (рис. 2.3).

При h ® 0 w ® 0, и второе слагаемое в выражении для удельной энергии сечения потока стремится к бесконечности, а с ним стремится к бесконечности и удельная энергия сечения потока. При этом кривая графика асимптотически приближается к оси абсцисс.

 

Рис. 2.3

 

При h ® ¥ второе слагаемое стремится к 0, а кривая графика удельной энергии сечения потока Э асимптотически приближается к прямой Э = h, так как при больших h

.

Так как функция, выражающая зависимость удельной энергии сечения потока от глубины непрерывна, существует некоторое значение глубины h, при котором удельная энергия сечения потока принимает минимальное значение.

Графическое изображение удельной энергии сечения потока в функции от глубины называется кривой удельной энергии сечения потока.

Критическая глубина.

Глубина h, при которой удельная энергия сечения потока при данном расходе Q принимает минимальное значение, называется критической глубиной и обозначается h_к.. Состояние потока при критической глубине называется критическим. Критическими называются и все гидравлические элементы потока, соответствующие его критическому состоянию. Они обозначаются с индексом "к" – v_к, w_к, R_к, C_к и т.д.

Критическая глубина потока может быть найдена как экстремум непрерывной функции Э = Э(h). Для этого приравняем нулю первую производную функции

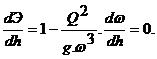
Из рис. 2.2 видно, что дифференциал площади живого сечения может быть представлен в виде d w = B. dh, где B - ширина потока (B = B(h)).

С учетом последнего выражения имеем

Выделяя в левую часть величины, зависящие от глубины h, уравнение для определения критической глубины h_к  окончательно получаем в виде

Для определения критической глубины можно использовать графики, один из которых представлен на рис. 2.4.

 

Рис. 2.4

Для русла прямоугольной формы B = const, w = B. h и уравнение для критической глубины принимает вид

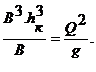
Отсюда получаются формулы для непосредственного вычисления h_к (с учетом, что расход Q = w_к. v_к = B. h_к. v_к)

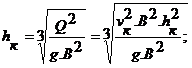
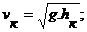
Вводя понятие удельного расхода жидкости на единицу ширины прямоугольного потока q = Q / B, выражение для критической глубины запишем в виде

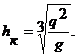
Для круглого сечения диаметром d (рис.2.5) безразмерное отношение w³/ B. d⁵ является функцией отношения h/ d.

             Рис. 2.5

 

Например, при h > d/2,  

По этим формулам составлены таблицы зависимости w³/ B. d⁵ от h/ d. С помощью этих таблиц по известному значению отношения Q/ g. d⁵ можно найти отношение h/ d, при котором выполняется равенство

и т.о. определить значение критической глубины h_к. Такие вычисления выполняются при расчете дорожных труб.

Для речных русел критическая глубина и скорость могут определяться следующим образом.

Форму долины реки часто представляют в виде параболы степени k_o

;

площадь живого сечения для такого русла выражается формулой

 

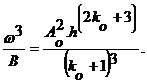
Из уравнения

или

получаем формулу для определения критической глубины и скорости

Критический уклон.

Для характеристики потока при неравномерном движении необходимо определение величины критического уклона.

Критическим уклоном называется такой уклон дна потока, при котором заданный расход проходит в условиях равномерного движения с критической глубиной, т.е. при котором нормальная глубина потока равна критической h_o = h_к. Вспомним, что нормальной глубиной называется глубина потока, с которой при данном уклоне дна I_o заданный расход Q проходит в условиях равномерного движения. Величина критического уклона в общем случае определяется из уравнения равномерного движения, которое при критических значениях элементов потока пишется следующим образом:

 откуда

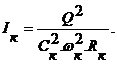
Подставив в эту формулу выражение для Q² из уравнения , а также учитывая, что R_к = w_к/c_к, получим следующую зависимость для определения критического уклона

Для суждения о состоянии потока и построения кривых свободной поверхности необходимо иметь данные о следующих основных элементах потока: критической глубине h_к, критическом уклоне I_к, нормальной глубине h_o и уклоне дна I_o.

 

Рис. 2.7

 

По уклону дна естественных и искусственных русел принято различать:   

- русла с горизонтальным дном при I_o = 0 (рис. 2 – 7,а);

- русла с прямым уклоном дна при I_o > 0 (рис. 2 – 7,б);

- русла с обратным уклоном дна при I_o < 0 (рис. 2 – 7,в).

Наиболее часто встречаются русла с прямым уклоном дна; искусственные русла (в частности дорожные трубы) нередко устраиваются с горизонтальным дном.

 При заданном расходе Q прямой уклон дна потока может быть равным критическому уклону I_к, меньшим или большим его. При уклоне дна, равном критическому для заданного расхода Q, нормальная глубина потока h_o равна критической глубине h_к. Если при том же расходе Q уменьшать уклон дна I_o, нормальная глубина h_o начнет возрастать, критическая же глубина h_к, зависящая для данного русла только от величины расхода Q, остается неизменной. Таким образом, при I_o < I_к будет h_o > h_к. С увеличением уклона дна сверх критического уклона глубина равномерного движения h_o становится меньше критической, т.е. при I_o  > I_к имеем h_o < h_к .

Формы свободной поверхности потока.

Соотношение между глубиной неравномерного движения h, нормальной глубиной h_o и критической глубиной h _к характеризует собой вполне определенные формы свободной поверхности потока.

При глубине потока большей критической h _к состояние потока называется спокойным. Спокойному состоянию потока отвечает верхняя ветвь кривой удельной энергии сечения (рис. 2 – 3). С увеличением глубины спокойного потока увеличивается и удельная энергия сечения. Примерами спокойных потоков являются равнинные реки с незначительными уклонами.

При глубине потока меньше критической h_к поток находится в бурном состоянии. На кривой удельной энергии сечения (рис. 2 – 3) бурному состоянию соответствует нижняя ветвь. С увеличением глубины потока удельная энергия сечения уменьшается. Горные реки с большими уклонами могут служить примером бурных потоков. В бурном состоянии поток обладает значительной энергией, главным образом за счет скорости течения. При этом происходит

интенсивный размыв дна и стенок русла. При устройстве искусственных водопропускных сооружений во избежание деформации русла бурные потоки стремятся превратить в спокойные путем выполнения ряда инженерных мероприятий, главным образом, устройством гасителей энергии различной конструкции.

Гидравлический прыжок

 

В заключение отметим, что переход потока из бурного состояния в спокойное происходит скачкообразно. Такое явление называется гидравлическим прыжком      (рис. 2.8).

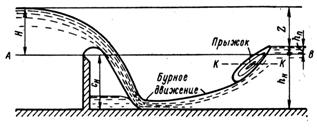
Рис. 2.8

 

5.3. ВОДОСЛИВОВЫ