Линия тока.
Движущуюся жидкость можно рассматривать как совокупное движение материальных точек.
Соединив линией все последующие по времени положения материальной точки, получим линию, которую называют линией тока (рис. 1.1).
Рис. 1.1. Линия тока
Т рубка тока и элементарная струйка.
Совокупность траекторий частиц жидкости, проходящих через какой-нибудь малый замкнутый контур образуют трубку тока, а множество траекторий частиц жидкости внутри трубки тока – элементарную струйку (рис. 1.2).
Рис. 1.2. Элементарная струйка
Вихревое движение.
Течение жидкости, совершающей вращательное движение называют вихревым. Вихревое движение характеризуется угловой скоростью вращения элементарной жидкой частицы. Линию, в каждой точке которой вектор вихря совпадает с направлением касательной к этой точке, называют вихревой линией.
Уравнение сплошности течения
Рассматривая отдельные элементарные струйки, предполагают, что они имеют неизменяемую форму во времени, обмен частицами жидкости между соседними элементарными струйками исключен, а скорости u одинаковы по всему поперечному сечению струйки d w, нормальному к направлению скорости u (рис. 1.3).
Рис. 1.3
Такое поперечное сечение называется живым сечением элементарной струйки.
Определим объем жидкости, проходящий через данное живое сечение d w элементарной струйки в единицу времени, который называется расходом струйки или элементарным расходом dQ. Поскольку скорость струйки u постоянна по всему сечению d w, то все частицы жидкости, находившиеся в плоскости живого сечения в момент времени t за какой-то элементарный промежуток времени dt проделают одинаковый путь dl. Это можно представить себе как объем жидкости dW, прошедший через живое сечение d w за время dt (рис. 1.3)
dW = d w dl.
Тогда объем жидкости, прошедший через живое сечение в единицу времени составит
Отсюда следует, что элементарный расход равен произведению скорости на площадь живого сечения струйки
(1 – 2)
Вследствие неразрывности потока жидкости элементарный расход остается постоянным по длине элементарном струйки, т.е.
dQ = Const.
Это условие для двух произвольно выбранных живых сечений струйки (например, сечений d w 1 и d w 2) можно записать в следующей виде:
dQ = u1.d w 1 = u2.d w 2 =Const. (1.3)
Полученное уравнение носит название гидравлического уравнения неразрывности элементарной струйки. Из него следует, что:
(1.4)
т.е. скорости в различных сечениях элементарной струйки обратно пропорциональны площадям живых сечений.
Понятие о потоке жидкости
В общем случае поток (например, поток воды в канале, трубе и т.п.), как уже отмечалось выше, можно представить как совокупность элементарных струек.
Рис. 1.4. Поток жидкости
Величину площади живого сечения w можно определить как сумму элементарных живых сечений отдельных струек в потоке (рис. 1.4)
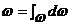. (1.5)
Распределение скоростей в плоскости живого сечениябывает,как правило, неравномерным.Так, на прямолинейных участках рек и каналов скорости течения воды у берегов меньше, чем на середине потока, а у поверхности больше, чем у дна (рис. 1.5,а),
Рис. 1.5
В круглой цилиндрической трубе в пределах прямолинейного участка скорость течения по оси трубы больше, чем у стенок (рис. 1.5, б).
Средней скоростью потока v называется такая скорость, с которой должны были бы двигаться все частицы жидкости через данное живое сечение потока, чтобы обеспечить тот же расход, который имеет место при действительном распределении скоростей по сечению потока.
Расходом потока Q называется объем жидкости, проходящий через данное живое сечение в единицу времени. Очевидно, величину расхода потока Q можно определить путем интегрирования элементарных расходов dQ. по всему живому сечению потока:
.
Заменив в этом выражении местные скорости u скоростью v, постоянной для данного живого сечения (v = Const), получим:
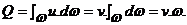
; (1.6)
т.е. расход потока в данном сечении равен произведению площади живого сечения на среднюю скорость потока.
Размерность расхода в системе СИ 
Кроме рассмотренных выше элементов потока: расхода Q, средней скорости v, площади живого сечения w, следует различать еще:
- смоченный периметр - c;
- гидравлический радиус - R;
- ширину потока на уровне свободной поверхности - B;
- среднюю глубину потока hср;
Рис. 1.6
Смоченным периметром c называется периметр живого сечения потока или часть его, непосредственно соприкасающаяся с ограждающими стенками потока (рис.1.6).
Отношение площади живого сечения к смоченному периметру называется гидравлическим радиусом
.
При напорном движении жидкости в круглой трубе
.
Средняя глубина потока hср равна отношению площади живого сечения w к его ширине на уровне свободной поверхности В
.
Если русло потока имеет значительную ширину при небольшой глубине, то можно принять (рис. 1.6)
.
Тогда на основании равенств и получим: 
.
1.2. ВИДЫ ДВИЖЕНИЯ ЖИДКОСТИ
