Цель работы – изучение крутильных колебаний вращающегося стола при разной массе системы и пружинах различной упругости
Приборы и принадлежности: лабораторный модуль
ЛКМ-3 с вращающимся столом, два круглых груза, груз наборный, нить длиной 45 см (красная), измерительная система ИСМ-1 (секундомер), нижний ролик на стойке с двумя осями, две пружины с балками, измерительная линейка.
Краткая теория
При вращательном движении твердого тела вокруг неподвижной оси каждая точка тела движется в плоскости, перпендикулярной оси, по окружности, центр которой лежит на оси. Линейная скорость точки тела v связана с угловой скоростью тела.
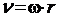 , (1)
, (1)
где r – расстояние от точки тела до оси вращения.
Кинетическая энергия тела равна сумме кинетических энергий всех частиц тела:
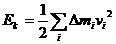 , (2)
, (2)
где 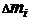 - элементарные массы, на которые мысленно разбито тело. Подставляя скорость vi из формулы (1) в (2), получим
- элементарные массы, на которые мысленно разбито тело. Подставляя скорость vi из формулы (1) в (2), получим
 (3)
(3)
Величина 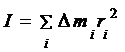 (4)
(4)
называется моментом инерции тела. Момент инерции характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела.
Выражение для кинетической энергии вращающегося тела вокруг неподвижной оси, исходя из формул (3) и (4), выглядит следующим образом:
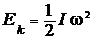 |
.
Для вычисления моментов инерции различных тел массу 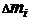 в формуле (4) выражают через плотность тела:
в формуле (4) выражают через плотность тела: 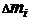 = ρ Δ Vi, где Δ Vi – элементарный объем тела, и переходят к пределу ΔVi → 0. Тогда получим
= ρ Δ Vi, где Δ Vi – элементарный объем тела, и переходят к пределу ΔVi → 0. Тогда получим
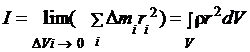 . (6)
. (6)
Теорема Штейнера устанавливает связь между моментом инерции тела Iс относительно оси, проходящей через центр инерции, и моментом инерции I этого тела относительно другой оси, параллельной первой.
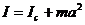 ,
,
где m – масса тела, а – расстояние между осями.
В настоящей работе измеряется момент инерции различных тел с помощью крутильного маятника. Этот маятник состоит из горизонтально расположенного поворотного стола, на котором могут закрепляться различные тела. На оси поворотного стола закреплен шкив радиусом R, с помощью которого столу может сообщаться вращательное движение. Через шкив перекинута нить, к концам которой прикреплены две пружины (рис. 1) c коэффициентами жесткости k 1 и k 2.
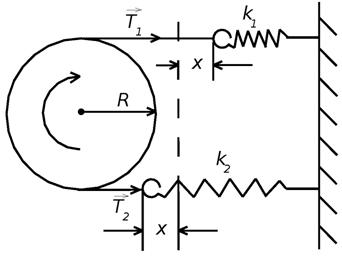
Рис. 1. Крутильный маятник
В положении равновесия силы натяжения нити по разные стороны от шкива одинаковы и равны упругим силам, которые согласно закону Гука
(F упр ) 0 = k 1 x 01 = k 2 x 02, (8)
где x01 и x02 - величины растяжения пружин.
При отклонении от положения равновесия поворотный стол совершает колебания под действием сил упругости двух пружин. Величина деформации одной пружины x1 = x01 + х, где х – отклонение от равновесного положения. Если нить нерастяжимая, то величина деформации другой пружины
х2 = х 02 – х.
Запишем выражение для потенциальной энергии деформации пружин следующим образом:
 (x 01 + x)2 (9)
(x 01 + x)2 (9)
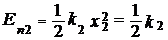 (x 02 - x)2 (10)
(x 02 - x)2 (10)
Если пренебрегать силами трения, то согласно закону сохранения механической энергии, полная механическая энергия, т. е. сумма кинетических и потенциальных энергий,
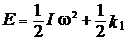 (x 01 + x)2 +
(x 01 + x)2 + 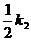 (x 02 - x)2 (11)
(x 02 - x)2 (11)
не зависит от времени. Значит, 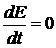 .
.
Вычисляя производную от выражения (11) по времени, получим
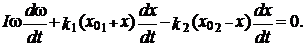 (12)
(12)
Если нить не проскальзывает по шкиву поворотного стола, то

 х = R j ,
х = R j ,
где j - угол поворота стола от положения равновесия;  . Учитывая условие равновесия (8) и определение угловой скорости
. Учитывая условие равновесия (8) и определение угловой скорости 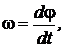 получим из уравнения (12)
получим из уравнения (12)

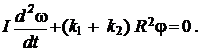 (13)
(13)
Обозначим  и
и
 – суммарный коэффициент жесткости двух пружин. Тогда уравнение (13) принимает вид дифференциального уравнения гармонических колебаний
– суммарный коэффициент жесткости двух пружин. Тогда уравнение (13) принимает вид дифференциального уравнения гармонических колебаний
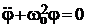 . (14)
. (14)
Решение этого уравнения:
j(t) = A cos(ωо t + α), (15)
где А – амплитуда колебаний, ωо - циклическая частота колебаний,
α - начальная фаза колебаний.
 Период колебаний
Период колебаний
(16)
.
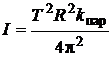 В данной работе находится момент инерции. Из формулы (16) следует
В данной работе находится момент инерции. Из формулы (16) следует
. ( 1 7)
Описание установки
Поворотный стол, смонтированный на модуле ЛКМ-3, снабжен датчиком вращения, который фиксирует повороты стола на один и более оборотов. Шкив стола 15 имеет диаметр 50 мм.
Две пружины закрепляются на осях нижнего блока 12 и прикрепляются к концам нити, перекинутой через шкив 15 (рис. 2). Таким образом, поворотный стол может совершать крутильные колебания вокруг своей оси под действием сил упругости пружин. Период колебаний зависит от упругости пружин k,момента инерции стола I и радиуса шкива R. На столе можно укреплять различные предметы и по периоду крутильных колебаний T определять момент инерции системы.
 |
Рис. 2. Крутильный маятник на модуле ЛКМ-3
Порядок выполнения работы
Задание I. Определение коэффициента упругости пружин
1. Подвесьте пружины с помощью балки 17 на оси блока 13 и закрепите на другом конце пружин груз т 1(см. рис. 2).
2. Измерьте линейкой расстояние x 1от основания стойки до нижнего края груза.
3. Измените массу груза на величину Δ m и измерьте новое расстояние х 2. Данные занесите в табл. 1. Рассчитайте коэффициент упругости пары пружин по формуле
 (18)
(18)
где g = 9,81 м/с – ускорение свободного падения.
4. Повторите измерения несколько раз. Рассчитайте среднее значение k пар . Данные занесите в табл. 1.
Таблица 1
| № п/п | т 1 | m 2 |  = т 1– m 2, кг = т 1– m 2, кг
| x 1 | х 2 | Δ х = х 2 – х 1, м | k пар, Н/м |
| … | |||||||
| Среднее | – | ― | - | - |
Задание II. Определение момента инерции методом
крутильных колебаний
1. Подготовьте измерительную систему ИСМ-1 к работе: подключите датчик угла поворота стола блока к разъему №1на задней стенке прибора, переключатель 1 поставьте в положение «К1», переключатель 4 – в положение «2», переключатель 5 – в положение «цикл», переключатель 8 – в положение «+» или переключатель 9 – в среднее положение. Включите питание модуля.
2. Накрутите нить (1,5 оборота) на шкив стола, диаметр которого D = 50мм (рис. 3), прикрепите к концам нити пружины. Закрепите пружины на осях 12 нижнего блока стойки 10.
3. Поверните стол так, чтобы в свободном положении указатель угла поворота стола находился вблизи нулевого деления шкалы 16.
4.
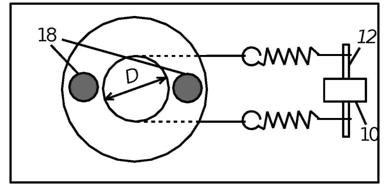 |
Нажмите кнопку 7 «готов» и приведите стол в колебательное движение с амплитудой 40 – 60 градусов.
Рис.3. Определение момента инерции маятника
5. Считайте с индикатора время одного полного колебания T.
 6. Рассчитайте момент инерции ненагруженного стола по формуле
6. Рассчитайте момент инерции ненагруженного стола по формуле
(19)
где R – радиус шкива стола (R = D / 2), k пар – коэффициент упругости двух пружин, соединенных параллельно. Данные занесите в табл. 2. Повторите измерения 5 – 7 раз.
Таблица 2
| № п/п | Т (c) | I o,кг м2 |
| … | ||
| среднее |
Задание III. Проверка теоремы Штейнера
1. Поместите в центре стола два цилиндрических груза 18 массой т цпо 500 г один над другим (точная масса грузов выгравирована на нижнем торце грузов). Повторите измерения момента инерции системы I сис (по п. 3 – 6 в задании II).
2. Рассчитайте момент инерции цилиндров по формуле
I ц = I сис – I о , (21)
где I 0 - момент инерции не нагруженного стола, измеренный в задании II.
3. Рассчитайте теоретический момент инерции цилиндров I теор относительно оси цилиндров по формуле
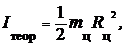 (22)
(22)
где т ц – суммарная масса цилиндров, R ц – радиус цилиндров
(R ц = 24 мм). Данные занесите в табл. 3.
4. Переместите цилиндры на одинаковое расстояние Δ х относительно оси вращения (шаг отверстий на вращающемся столе Δ х =20мм).Измерьте период колебаний m 2 системы, соответствующий новому положению цилиндров. Данные занесите в табл. 3.
Таблица 3
| № п/п | Δ х | Δ х 2 | T сис | T сис2 | т ц = т 1+ m 2 | I сис | I о | I теор |
| … |
5. Рассчитайте момент инерции системы I сис по формуле
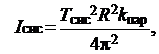 (23)
(23)
где k пар – коэффициент упругости пары пружин (см. задание I),
R –- радиус шкива стола.
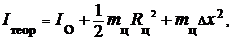 6. Рассчитайте теоретический момент инерции системы по формуле
6. Рассчитайте теоретический момент инерции системы по формуле
где I 0 – момент инерции не нагруженного стола (см. задание II), т ц – суммарная масса цилиндров, R ц – радиус цилиндров
(R ц = 24 мм).
7. Повторите измерения и расчеты по п. 1– 6 для всех положений цилиндров. Данные занесите в табл. 3.
8. Постройте график зависимости момента инерции I сиси I теор от квадрата расстояния от оси вращения до центра грузов Δ х 2.
Контрольные вопросы
1. Дайте определение динамических характеристик вращательного движения: момента силы – М, момента инерции – I, момента импульса – L.
2. Запишите аналитические выражения для момента инерции частицы и твердого тела. Как производится расчет момента инерции обруча, стержня, диска?
3. В чем состоит суть теоремы Штейнера?
4. Получите основное уравнение динамики вращательного движения.
5. Получите уравнение колебаний крутильного маятника.
6. Как рассчитать период колебаний крутильного маятника?






