1. Два маленьких шарика массой m = 10 г каждый скреплены тонким невесомым стержнем длиной l = 20 см. Определить момент инерции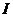 
системы относительно оси, перпендикулярной стержню и проходящей через центр масс.
2. Два шара массами m и 2 m (m = 10 г) закреплены на тонком невесомом стержне длиной l = 40 см так, как это указано на рис. 4. Определить момент инерции 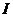системы относительно оси, перпендикулярной стержню и проходящей через его конец. Размерами шаров пренебречь.
3. Два шара массами 2 m и m (m = 20 г) закреплены на тонком невесомом стержне длиной l = 1 м так, как это показано на рис. 5 Определить момент инерции 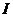системы относительно оси, перпендикулярной стержню и проходящей через его конец. Размерами шаров пренебречь.
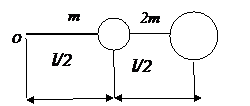
Рис. 4 (к задаче 2) Рис. 5 (к задаче 3)
4. Определить момент инерции трехатомной молекулы H2O (рис. 6) относительно оси y, проходящей через центр масс молекулы. Межъядерное расстояние AB обозначено d = 0,097 нм, α = 104о30' .
5. Определить момент инерции трехатомной молекулы SO2 (рис. 6) относительно оси x, проходящей через центр масс молекулы
(d = 0, 145 нм, α = 124о).
Рис. 6 (к задаче 6)
6. Определить момент инерции тонкого однородного стержня длиной l = 30 см и массой m = 100 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/3 его длины. Определить момент инерции 
тонкого однородного стержня длиной l = 60 см и массой m = 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на
a = 20 см от одного из его концов.
7. На концах тонкого однородного стержня длиной l и массой 3 m прикреплены маленькие шарики массами m и 2 m. Определить момент инерции такой системы относительно оси, перпендикулярной стержню и проходящей через точку, лежащую на середине стержня (рис. 7).
Рис. 7 (к задаче 7)
8. Вычислить момент инерции J проволочного прямоугольника со сторонами a = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью 0,1 кг/м.
9. Определить момент инерции проволочного равностороннего треугольника со стороной a = 10 см относительно: оси, лежащей в плоскости треугольника и проходящей через его вершину и середину противоположной стороны.
10. Определить момент инерции кольца массой m = 50 г и радиусом R = 10 см относительно оси, касательной кольцу.
11. Диаметр диска d = 20 см, масса m = 800 г. Определить момент инерции диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.
12. Найти момент инерции плоской однородной прямоугольной пластины массой m = 800 г относительно оси, совпадающей с одной из ее сторон, если длина a другой стороны равна 40 см.
13. Определить момент инерции тонкой плоской пластины со сторонами a = 10 см и b =20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью 1,2 кг/м2.
14. В однородном диске массой m = 1 кг и радиусом R = 30 см вырезано круглое отверстие диаметром d =20 см, центр которого находится на расстоянии l = 15 см от оси диска (рис. 8). Найти момент инерции полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
15. На однородный сплошной цилиндр массой M и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массой m (рис.9). В момент времени t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени модуля угловой скорости цилиндра.
Рис. 8 (к задаче 14) Рис. 9 (к задаче 15)
16. Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m 1 = 0,3 кг и m 2 = 0,5 кг. Определить силы T 1 и T 2 натяжения нити по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.
17. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m 1 = 100 г и m 2 = 110 г. С каким ускорением будут двигаться грузы, если масса блока m = 400 г. Трение при вращении блока ничтожно мало.
18. Два тела массами m 1 = 0,25 г и m 2 = 0,15 г связаны тонкой нитью, переброшенной через блок (рис. 10). Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой m1.
С каким ускорением движутся тела, и каковы силы T 1 и T 2 натяжения нити по обе стороны блока? Коэффициент трения µ тела о поверхность стола равен 0,2. Масса m блока равна 0,1 г, и ее можно считать равномерно распределенной по ободу. Массой нити и трением в подшипниках оси блока пренебречь.
19. Однородный сплошной цилиндр массой m = 1 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис.11). Цилиндр отпускают без толчка. а) За сколько времени t цилиндр опустится на расстояние y =50 см? б) Какое натяжение F испытывает при опускании цилиндра каждая из нитей?
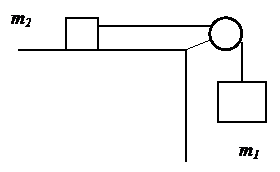
Рис. 10 (к задаче 18) Рис. 11 (к задаче 19)
Лабораторная работа № 5
ФИЗИЧЕСКИЙ МАЯТНИК
Цель работы – изучение физического маятника, определение ускорения свободного падения.
Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.
Краткая теория
Физический маятник – твердое тело, которое может совершать колебания под действием силы тяжести относительно неподвижной оси O(рис. 1).
Рис. 1. Физический маятник
Запишем основное уравнение динамики вращательного движения.
.
I β = М, (1)
где I – момент инерции маятника;
– угловое ускорение, φ – угол отклонения маятника от положения равновесия, М - сумма проекций моментов сил на направление оси вращения. Если момент сил трения много меньше момента силы тяжести, то
M = - mga ×sinj,, (2)
где т – масса маятника, g –- ускорение свободного падения, а –- расстояние от оси вращения до центра тяжести.
Уравнение движения (1) с учетом (2) примет вид
I j = - mga ×sinα
где ωо2 = (mga)/ I,тогда получим уравнение:
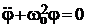. (3)
Уравнение (3) является линейным дифференциальным уравнением относительно функции φ(t).
Если амплитуда колебаний физического маятника не мала, дифференциальное уравнение (3) не будет линейным. Для больших углов отклонений маятника период Т начинает зависеть от амплитуды колебаний φ m . Эту зависимость можно представить суммой бесконечного ряда, первые слагаемые которого равны
. (4)
При малых колебаниях угол φ мал, поэтому sinφ ≈ φ и уравнение (3) становится дифференциальным уравнением гармонических колебаний
. (5)
Решение этого уравнения:
j = j m cos(ω0t + α), (6)
где α - начальная фаза колебаний, ωо = 2π /Т - циклическая частота колебаний.
Запишем формулу периода малых колебаний, как
(7)
Получим зависимость периода малых колебаний от расстояния а. Момент инерции, согласно теореме Штейнера, равен
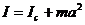, (8)
где I с - момент инерции маятника относительно оси, проходящей через центр масс. Подставляя (8) в (7), получим
(9)
Согласно этой формуле период колебаний Т одинаков при двухразличных значениях а (рис. 2): Т 1 = Т 2 при
, откуда
. (10)
Подставим (10) в формулу (9). Получим
(11)
Величина 
(12)
называется приведенной длиной физического маятника.
Сравнивая формулы (11) и (7) получим
(13)
Формула для периода малых колебаний маятника будет иметь следующий вид
. (14)
В данной работе с помощью физического маятника находится ускорение свободного падения g,которое исходя из уравнения (14),
. (15)
Приведенная длина 
находится из формулы (12), в которой а 1и а 2определяются из графика зависимости Т от а, построенного на основе результатов эксперимента.
Для уменьшения погрешности измерения в эксперименте измеряют период колебаний маятника относительно осей, находящихся по обе стороны от центра тяжести. На рис. 2 представлена теоретическая зависимость периода колебаний от параметра a, которая зеркально симметрична относительно оси Т.
 |
Рис. 2. Зависимость периода колебаний маятника от параметрa a
На рисунке приведенная длина маятника L np = a 1 + a 2 равна расстоянию между точками А ̀В или В̀ А.
Описание установки
Физический маятник представляет собой твердое тело, в нашем случае – стержень 12, с отверстиями, который монтируется на блоке 11, закрепленном на стойке 10 модуля ЛКМ-3 так, чтобы ось блока не проходила через центр масс (рис. 3). В этом случае стержень может совершать колебания в поле силы тяжести. На оси стержень закрепляют пластиковым фиксатором 13.
Рис. 3. Физический маятник на модуле ЛКМ-3
Задание I. Измерение ускорения свободного падения
1. Подготовьте измерительную систему ИСМ–1 к работе: подключите датчик угла поворота блока к разъему 1 на задней стенке прибора, переключатель 1 поставьте в положение «К1», переключатель 4 – в положение «2», переключатель 5 – в положение «цикл», переключатель 8 – в положение «+» или «–», переключатель 9 – в среднее положение. Включите питание модуля.
2. Закрепите стержень на оси блока за крайнее отверстие так, чтобы прорезь в блоке находилась вблизи нулевого деления шкалы. Примите это положение маятника за начальное х = 0. Приведите маятник в колебательное движение с амплитудой
(5 ÷ 10)°. Считайте с измерителя периода колебаний время одного полного периода Т. Данные занесите в табл. 1.
3. Переместите маятник на одно отверстие (Δ x = 20 мм) и проведите аналогичные измерения периода колебаний для всех отверстий стержня.
4. Постройте график зависимости периода колебаний физического маятника Т от координаты точки подвеса х.
Таблица 1
| x (см) | 0 | … | 32 |
| T (c) |
5. На графике (см. рис. 2)найдите расстояние между точками маятника x 1и x 2, cоответствующими одинаковому периоду колебаний (x2 – x1 = L np) в трех пяти местах графика. Заполните табл. 2.
Таблица 2
| I | x 1 | x 2 | Т i (c) | L np i (м) | gi (м/с) | gi – < g> | (gi– < g>)2 |
| … | |||||||
| Среднее | ― | ― | ― | ― | ― | ― | |
| Сумма | ― | ― | ― | ― | ― |
6. Рассчитайте ускорение свободного падения по формуле (15).
7. Рассчитайте абсолютную и относительную погрешность измерений g.
Запишите результат в стандартном виде
g = (< g > ± Δ g) (м/с2), ε =... % при α= 0,95.
Задание II. Исследование ангармонических колебаний
1. Закрепите стержень на оси за второе отверстие (х = 2 см). Поставьте переключатель 5 в положение «однокр». Нажмите кнопку 7 «готов». Отведите маятник на угол 10 и плавно отпустите его. Считайте показания измерителя периода колебаний Т. Данные занесите в табл. 3.
Таблица 3
| φ m | 10º | 20º | … | 90º |
| Т (c) |
2. Повторите измерения периода колебаний, изменяя амплитуду колебаний φ m в пределах от 10° до 90° с шагом в 100-200
3. Постройте график зависимости периода колебаний Т от амплитуды колебаний φ m.
Контрольные вопросы
1. Получите уравнение гармонических колебаний для случая колебаний груза на пружинке. Дайте определение параметрам колебательного движения: смещению из положения равновесия, скорости и ускорению материальной частицы. Запишите закон изменения кинетической, потенциальной и полной энергии частицы?
2. Получите уравнение колебаний математического и физического маятников. Запишите выражения для периода, частоты колебаний и приведенной длины физического маятника.
3. В чем состоит особенность оборотного физического маятника. Можно ли использовать произвольный физический маятник для определения ускорения свободного падения?
