Измерение ускорения свободного падения  с  помощью машины Атвуда

Цель работы – изучение динамики поступательного движения связанной системы тел с учетом сил трения.

Приборы и принадлежности: машина Атвуда, смонтированная на лабораторном модуле ЛКМ–3, набор грузов и перегрузов, нить с крючками длиной 60 см (зеленая), измерительная система ИСМ–1 (секундомер).

Введение

 

Рассмотрим движение механической системы, состоящей из вращающегося легкого блока, через который перекинута нить с привязанными грузами массами   m ₁и   т ₂(т ₁ < т ₂) (рис. 1).

Запишем второй закон Ньютона в векторной форме для движения грузов

                 (1)          

Если нить нерастяжимая, то ускорения грузов 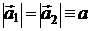. Спроецируем векторные уравнения (1) на направление ускорения движения каждого груза.

                             (2)

Из уравнений (2) получим

                                                                                                (3)

 

Разность сил натяжения (T ₂ – Т ₁ ) зависит от меры инертности блока (момента инерции) и трения в подшипниках блока.

В предельном случае отсутствия сил трения и нулевой массы блока и нити Т ₂ = Т ₁ ,

Поэтому 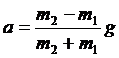 ,                                                (4)

а ускорение свободного падения 

                .                                          (5)

 

Учтем влияние сил трения в подшипниках оси блока (пренебрегая массой блока). Введем в уравнение (3) вместо разности Т ₂– Т ₁«эффективную» силу сопротивления F.

,                                        (6)

При сухом трении в подшипниках и незначительном изменении массы грузов m ₁и m ₂   в первом приближении можно считать, что отношение   не зависит от масс грузов, а ускорение а зависит от величины k = (т ₂ – m ₁ )/ (m ₁ + m ₂ ).

 

Кинематическая связь ускорения   а грузов с угловым ускорением β блока при отсутствии проскальзывания нити

                                      а = β R,                                                            (7)

где R – радиус блока.

При равноускоренном движении угол поворота блока φ при начальной угловой скорости ω_о = 0 

 

j     .                                          (8)

 

 Из формул (7) и (8) следует

 

                                 (9)

 

Описание установки

 

 

Машина Атвуда представляет собой блок, закрепленный на стойке 1, через который перекинута нить. К концам нити подвешены грузы m ₁и т ₂(рис.2). Вращение блока регистрируется фотодатчиком, который фиксирует поворот блока на один и более оборотов.

 

 

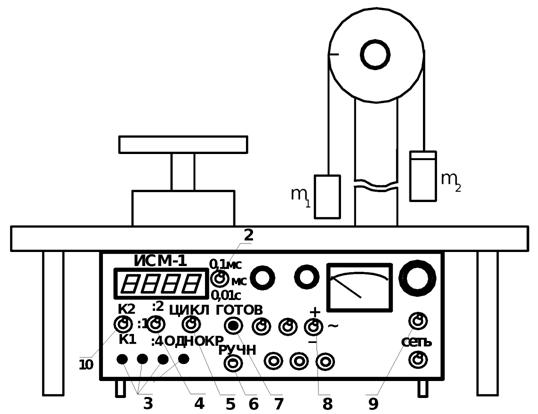Рмс. 2. Машина Атвуда на модуле ЛКМ-3

 

 

Задание I. Измерение ускорения свободного падения

 

1. Подключите датчик угла поворота блока к разъему № 2 на задней стенке модуля ИСМ – 1. Переключатель 10 переведите в положение К2. Переключатель 4 – в положение «:1», переключатель 5 - в положение «однокр», переключатель 8 - в положение «+» или «–», переключатель 9 – в среднее положение. Включите переключателем «сеть» питание модуля.

Перекиньте нить через большой блок, радиус которого R = 25 мм, и закрепите на концах нити грузы примерно одинаковой массы m ₁и т ₂ (m ₁≈ т ₂≈100 г, точное значение массы грузов выгравировано на каждом грузе), убедитесь, что грузы в свободном состоянии находятся в равновесии. Массу т ₂ увеличьте на 10 г с помощью перегрузка. Значение массы грузов m ₁и т ₂ с точностью до десятых долей грамма занесите в таблицу. Переведите груз m ₁в нижнее положение и остановите качание второго груза. Вращая блок, добейтесь срабатывания датчика угла поворота, о чем свидетельствует загорание индикатора 3, при этом прорезь на блоке будет находиться вблизи нулевой отметки шкалы блока. Нажмите кнопку 7 «готов» и отпустите груз m ₁. Система грузов придет в движение и таймер модуля ИСМ–1 зафиксирует время одного оборота блока в секундах или в миллисекундах в зависимости от положения переключателя 2. Результат измерения занесите в таблицу.

 

                                                                              Таблица

№	t	t 2	m 1	m 2	a	g	k
1
…
среднее
…
среднее
среднее	–	–	–	–	–		–

 

 

2. Рассчитайте ускорение грузов по формуле (9).

3. Рассчитайте ускорение свободного падения   g по формуле (5).

4. Повторите измерения и расчеты по пп.2–4 не менее 5 раз и рассчитайте среднее ускорение грузов а и среднее ускорение свободного падения g.

5.Замените перегрузок 10 г на другой, массой 20 г. Повторите измерения по пунктам 2-5.

6. Проведите те же опыты по п. 2 – 6 с перегрузками в 10 г и 20 г, изменив массу наборных грузов вдвое  (m ₁≈ т ₂≈ 200 г).

7. Найдите среднее значение ускорения свободного падения g по всем измерениям.

8. Оцените абсолютную и относительную погрешность нахождения ускорения свободного падения g по методу Стьюдента. Результат запишите в стандартном виде:

        g = (< g > ± Δ g) (м/с²), ε =... %   при   а = 0,95.

Задание II. Определение ускорения свободного падения    

с учетом трения в подшипниках оси блока

Разность масс грузов в нашем эксперименте составляет всего 2 – 10 % от их суммарной массы (при большей разности масс движение грузов становится слишком быстрым, что приводит к выходу из строя установки). При этом на результаты эксперимента заметно влияет трение в подшипниках оси блока. Введя в уравнение движения грузов некоторую «эффективную» силу сопротивления F, получим уравнение движения грузов с учетом силы трения в подшипниках оси блока

a (m ₁ + m ₂) = (m ₂   –  m ₁) g - F,                       (10)

откуда

 (11)

                                                                            

Отношение в случае сухого трения в первом приближении постоянно. Рассчитайте коэффициенты 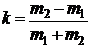 для каждого значения массы и заполните таблицу.

Построив график зависимости ускорения   а от величины k  и убедившись в том, что эта зависимость линейная, найдите g как угловой коэффициент графика. Ускорение свободного падения можно найти так же как

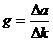                                   ,                                   (12)

где Δ a – разность между ускорениями системы при разных массах, а разность Δ k = k ₂ – k ₁ вычисляется для соответствующих значений масс.

Сравните результаты, полученные в первом и втором заданиях.

Отношение   можно найти как экстраполированное значение произведения   k ∙ g,при котором а = 0.

Контрольные вопросы

1. Дайте определение кинематическим характеристикам материальной точки, движущейся прямолинейно: траектории, перемещению, пути, скорости, ускорению.

2. Дайте определение кинематическим характеристикам материальной точки, движущейся по окружности: углу поворота, угловой скорости, угловому ускорению. Какова связь между линейными и угловыми кинематическими характеристиками?

3. Что изучает динамика поступательного движения? Как вводится понятие силы, действующей на частицу, и массы частицы в динамике? Записать уравнение движения материальной частицы.

4. Как изменяется закон сухого трения в зависимости от внешнего воздействия на тело, находящегося на поверхности другого тела? От каких факторов зависит коэффициент трения? Другие виды трения. Анализ движения тела по наклонной плоскости при разных углах наклона.

5. Выведите основную рабочую формулу (5).