1. Ускорение свободного падения у поверхности Луны в 6 раз меньше ускорения свободного падения у поверхности Земли.
Во сколько раз выше может прыгнуть человек на Луне, чем на Земле?
2. Радиус Луны R л примерно в 3,7 раза меньше радиуса Земли R з,,,а масса Луны m л в 81 раз меньше массы Земли m з . Найти ускорение свободного падения g л у поверхности Луны.
3. На какой высоте над полюсом Земли ускорение свободного падения на убывает в 2 раза?
4. Радиус Солнца R с примерно в 110 раз больше радиуса Земли R з, а средняя плотность Солнца относится к средней плотности Земли как 1:4. Найти ускорение свободного падения у поверхности Солнца.
5. Радиус R малой планеты равен 250 км, средняя плотность
3 г/см3. Определить ускорение свободного падения g на поверхности планеты.
6. Через неподвижный блок перекинута нить, к концам которой привязаны грузы массами m 1= 2 кг и m 2 = 3 кг (см. рис.1). Найти ускорение грузов. Массой блока пренебречь, нить считать невесомой и нерастяжимой.
7. Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами М. Одновременно, на каждый из грузов кладут по перегрузку: справа – массой 3 m, слева – m (рис 3.). Определить ускорение системы.
8. Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой m = 5 кг каждый (рис.4). Найти ускорение системы и силу натяжения нити между грузами 1 и 2.
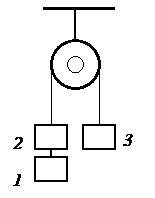
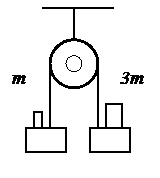
Рис. 3 (к задаче 7) Рис. 4 (к задаче 8)
9. На углу гладкого стола укреплен неподвижный блок (рис. 5), через него перекинута нить, к концам которой привязаны грузы. Масса груза, лежащего на столе m 1 = 5 кг, масса второго груза m 2 = 2 кг. С каким ускорением движутся грузы?
10. Два груза массами m 1 и m 2 соединены легкой нерастяжимой нитью (см. рис. 5). Коэффициент трения между грузом и столом μ. Определить условие, при котором грузы будут двигаться.
11. На наклонной плоскости с углом α лежит брусок массой m 1. Груз массой m 2 присоединен к бруску при помощи нити, перекинутой через блок (рис. 6). Определить ускорение тел и силу натяжения нити.
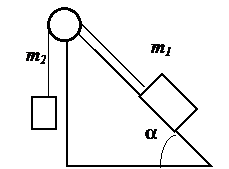

Рис. 5 (к задаче 10) Рис. 6 (к задаче 11)
12. Три груза m, m и 4 m, где m = 5 кг, соединены невесомыми нерастяжимыми нитями (рис. 7). Коэффициент трения между грузами и горизонтальной поверхностью µ = 0,3. Определить силы натяжения нитей.
 13. Два груза массами m 1 = 100 г и m 2 = 50 г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис. 8). Грузы прижимаются друг к другу с постоянными силами F = 1 Н. Коэффициент трения между ними µ = 0,1. Найти ускорение, с которым движутся грузы.
13. Два груза массами m 1 = 100 г и m 2 = 50 г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис. 8). Грузы прижимаются друг к другу с постоянными силами F = 1 Н. Коэффициент трения между ними µ = 0,1. Найти ускорение, с которым движутся грузы.

Рис. 7 (к задаче 12) Рис. 8 (к задаче 13)
14. Колесо радиусом R = 10 см вращается с угловым ускорением 3,14 рад/с. Найти для точек обода к концу первой секунды угловую скорость.
15. Вал вращается с частотой 180 об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением 3 рад/с2. Через какое время вал остановится?
16. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
17. Вал вращается с частотой 180 об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением 3 рад/с2. Через какое время вал остановится?
18. Точка движется по окружности радиуса R = 20 см с постоянным тангенциальным ускорением 5 см/с2. Через какое время t после начала движения нормальное ускорение будет равно тангенциальному ускорению?
19. Колесо радиусом R = 10 см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 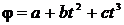 ,, где a, b, c – константы, b = 2 рад/с2, c = 1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую и линейную скорости, б) угловое ускорение.
,, где a, b, c – константы, b = 2 рад/с2, c = 1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую и линейную скорости, б) угловое ускорение.
20. На наклонной плоскости с углом при основании α находится доска массой M и на ней брусок массой m (M > m) (рис. 9). Коэффициент трения между доской и плоскостью μ, между доской и бруском –2µ. Определить ускорение этих тел. При каком отношении масс тела будут находиться в равновесии?
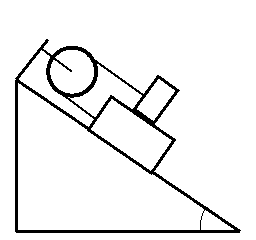

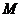
α
Рис. 9 (к задаче 20)
Лабораторная работа № 4
МАЯТНИК ОБЕРБЕКА
Цель работы – изучение основного закона динамики вращательного движения, определение момента инерции системы грузов.
Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, два круглых груза, груз наборный, нить длиной 55 см с крючком (синяя), измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.
Краткая теория
Основной закон динамики вращательного движения твердого тела относительно неподвижной оси
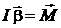 (1)
(1)
связывает кинематическую характеристику движения – угловое ускорение 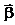 с динамическими характеристиками – моментом силы
с динамическими характеристиками – моментом силы 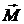 и моментом инерции I (рис. 1).
и моментом инерции I (рис. 1).
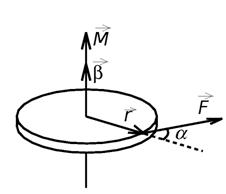
Угловое ускорение характеризует изменение угловой скорости во времени и направлено, как и момент силы, вдоль оси вращения.
Рис. 1. Момент M силы F
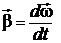 . (2)
. (2)
Угловое ускорение связано с касательной составляющей линейного ускорения а τточки вращающегося тела соотношением
 , (3)
, (3)
где r –- кратчайшее расстояние от этой точки до оси вращения.
Моментом силы в общем случае называют векторную величину
 , (4)
, (4)
где  – сила, лежащая в плоскости, перпендикулярной оси вращения;
– сила, лежащая в плоскости, перпендикулярной оси вращения; 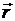 – вектор, соединяющий точку на оси c точкой приложения силы.
– вектор, соединяющий точку на оси c точкой приложения силы.
В уравнении (1) 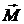 – сумма составляющих моментов сил вдоль направления оси вращения.
– сумма составляющих моментов сил вдоль направления оси вращения.
Момент инерции I характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела. Момент инерции равен сумме произведений элементарных масс Δ mi, на которые мысленно разбито тело, на квадрат их расстояний до оси вращения
I =ΣΔ mi ri . (5)
Выражая Δ mi через плотность тела: Δ mi = ρ Δ Vi,где Δ Vi – элементарный объем тела, и переходя к пределу при Δ Vi → 0, получим
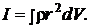 (6)
(6)
Формула (6) позволяет теоретически найти момент инерции любого тела. Например, момент инерции тонкого однородного стержня длиной l и массой т относительно оси, проходящей перпендикулярно стержню через его центр,
I = т l 2 / 12.
Теорема Штейнера устанавливает связь между моментом инерции I с твердого тела относительно оси, проходящей через центр инерции, и моментом инерции относительно другой оси, параллельной первой
I = I с + та2 , (7)
где а – расстояние между осями, т – масса тела.
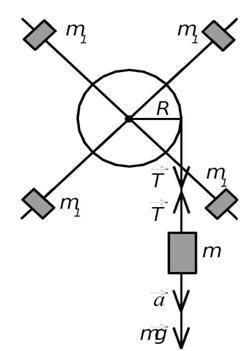
В настоящей работе экспериментально находится момент инерции маятника Обербека (рис.2). Он состоит из блока радиусом R, который может вращаться вокруг неподвижной горизонтальной оси. К блоку прикреплены симметрично относительнооси стержни, на каждом из которых могут свободно перемещаться грузы массами m 1, что дает возможность изменять момент инерции маятника. Грузы m 1 устанавливаются на одинаковом расстоянии от оси, так что центр инерции всей вращающейся части маятника находится на оси вращения.
.
Рис. 2. Маятник Обербека
К концу нити прикреплен груз массой m. Из закона динамики вращательного движения следует
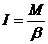 . (8)
. (8)
Момент силы М, создающийся силой натяжения нити, исходя из (4)
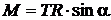 , (9)
, (9)
где α – угол между вектором  и отрезком R на рис. 2, равный 90°; sin α= 1.
и отрезком R на рис. 2, равный 90°; sin α= 1.
Запишем второй закон Ньютона для поступательного движения груза m в проекции на направление ускорения а,
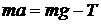 . (10)
. (10)
В этой формуле сила натяжения нити T, действующая на груз, по модулю равна силе натяжения нити, действующей на блок в формуле (9) (поэтому они обозначены одинаково). Это справедливо, если массой нити можно пренебречь по сравнению с массой груза т.
Из (9) и (10) получим
 . (11)
. (11)
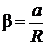 Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима.
Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима.
Тогда из (3) следует , (12)
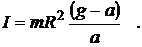 (13)
(13)
Подставляя (11)и(12)в (8), получим
Из этой формулы следует, что ускорение (а) не зависит от времени, так как все остальные величины в этом уравнении постоянны, значит, движение маятника будет равноускоренным и при нулевой начальной скорости.
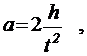 (14)
(14)
где h – путь, пройденный грузом т за время t.
В данной работе измеряется время одного полного оборота блока, и за это время груз массой m пройдет путь
h =2π R. (15)
Подставив (14) и (15) в (13), получим формулу для вычисления момента инерции маятника
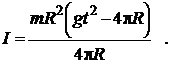
(16)
Момент инерции маятника Обербека будет изменяться при изменении расстояния r от оси вращения маятника до центров грузов массами m 1, перемещаемых вдоль стержней.
Согласно теореме Штейнера (7)
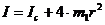 , (17)
, (17)
где Ic – момент инерции всей вращающейся части маятника при условии, что центры грузов m 1находились бы на оси вращения.
Из (17) следует, что зависимость 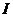 от
от 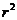 – линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.
– линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.
Описание установки
Маятник Обербека монтируется на блоке 11, закрепленном на стойке 10 модуля ЛКМ–3 (рис. 3). К блоку радиусом 25 мм прикрепляют нить, к концу которой подвешивают наборный груз массой т = 100 ÷ 200 г. На ось блока через среднее отверстие надевают стержень 12 и закрепляют его пластиковым фиксатором 13. Вращая стержень, накручивают на блок нить и поднимают груз так, чтобы он не касался стержня. При опускании груза нить приведет во вращательное движение стержень. После полного раскручивания нити стержень, продолжая вращательное движение, накрутит нить на блок и поднимет груз. При этом вращательное движение прекратится – система перейдет в начальное состояние.
Время опускания и подъема груза (период колебаний маятника Обербека) зависит от многих параметров установки: длины нити, массы груза т, момента инерции стержня и блока, радиуса блока (от сил трения, толщины и массы нити, которыми мы в данной работе пренебрегаем).
Порядок выполнения работы
Задание I. Определение момента инерции стержня и блока
Подготовьте измерительную систему ИСМ–1 к работе: подключите датчик угла поворота блока к разъему 1 на задней стенке прибора, переключатель 1 поставьте в положение «К1», переключатель 4 – в положение «:1», переключатель 5 – в положение «однокр», переключатель 8 – в положение «+» или «–», переключатель 9 – в среднее положение. Включите питание модуля.
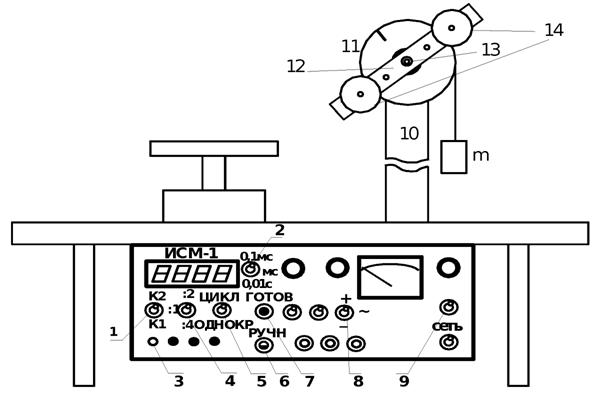 Рис. 3. Маятник Обербека на модуле ЛКМ-3
Рис. 3. Маятник Обербека на модуле ЛКМ-3
1. Закрепите конец нити на блоке так, чтобы нить не мешала креплению стержня и могла накручиваться на большой блок
(R = 25 мм). Укрепите стержень на оси блока, пропустив ось блока через середину стержня, и зафиксируйте его пластиковым фиксатором.
2. Накрутите нить на блок и прикрепите наборный груз т к свободному концу нити.
3. Поверните блок 11 со стержнем 12 так, чтобы прорезь блока совпала с нулевым делением шкалы и добейтесь срабатывания индикатора датчика угла поворота 3. Нажмите кнопку 7 «готов» и осторожно, без толчка, отпустите маятник, который под действием груза придет в движение. После одного полного оборота сработает датчик угла поворота блока и на индикаторе появится значение времени поворота в секундах или миллисекундах в зависимости от положения переключателя 2. Время и массу груза занесите в табл. 1.
Таблица 1
| № п/п | т | T | I | I – < I > | (I – < I >)2 |
| … |
| ||||
| … | |||||
| среднее | ― | ― | ― | ― | |
| сумма | ― | ― | ― | ― |
4. Рассчитайте по формуле (16) суммарный момент инерции I стержня блока.
5. Рассчитайте абсолютную и относительную погрешности измерения момента инерции I системы по методу Стьюдента для прямых измерений. Результат запишите в стандартном виде:
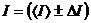 кг-м2; ε =...% при α = 0,95.
кг-м2; ε =...% при α = 0,95.
Задание II. Измерение момента инерции маятника Обербека в зависимости от положения грузов на стержне
1. Закрепите на стержне 12 симметрично относительно оси вращения два круглых груза 14 (см. рис. 3). Занесите в табл. 2 расстояние от оси вращения до центра грузов r, и массу наборного груза т.
2. Измерьте момент инерции системы так, как это описано в задании I. Данные занесите в табл. 2.
Таблица 2
| № п/п | т | T | r | r 2 | I |
Перемещая грузы 14 по стержню 12, повторите измерения момента инерции I для всех положений грузов (расстояние между отверстиями на стержне d = 20 мм).
Постройте график зависимости момента инерции I от квадрата расстояния от оси вращения до центра грузов r 2.
Контрольные вопросы
1. Дайте определение динамических характеристик вращательного движения: момента силы М, момента инерции I, момента импульса L.
2. Вывод основного уравнения динамики вращательного движения.
3. Вывод основной рабочей формулы (16).
4. Выражения для момента инерции материальной частицы, стержня, диска относительно оси, проходящей через центр масс. Как определяется момент инерции относительно произвольной оси? Теорема Штейнера.
5. Провести аналитический расчет момента инерции маятника Обербека. Как рассчитать период колебаний маятника Обербека?






