1. Подключите выносной пульт-кнопку к разъему № 1, расположенному на задней стенке прибора.
2. Поставьте органы управления прибором в соответствующие положения: а) переключатель количества измеряемых циклов 4 – «1»; б) переключатель циклического или однократного измерения 5 – «ОДНОКР»; в) включатель гироскопа 9 – в среднее положение.
3. Включите питание прибора.
4. Подготовьте прибор к измерению промежутков времени: нажмите кнопку 7 «ГОТОВ».
5. Один студент берет в руки выносной пульт - кнопку, а другой нажимает кнопку ручного запуска измерителя времени 6.
6. Первый студент, услышав звуковой сигнал включения измерителя, нажимает кнопку выносного пульта. На индикаторе высвечивается время реакции первого студента на звуковой сигнал.
7. Время реакции занесите в таблицу. Повторите измерение времени реакции человека по п.4 – 7 пять-семь раз.
Таблица
| № п/п | ti | ti -< t> | (ti -<t>)2 |
| 1 | |||
| … | |||
| Σ | - | ||
| Среднее | - | - |
8. Рассчитайте среднее время реакции человека по формуле
 |
,
где n – количество измерений.
9. Рассчитайте абсолютную погрешность Δ t измерения по формуле
 |
,
где τ(α, n) – коэффициент Стьюдента, зависящий от надежности α и количества измерений п (см. приложение в конце сборника).
 |
10. Рассчитайте относительную погрешность измерения по формуле
11. Запишите результат измерений в стандартном виде
 , с
, с 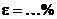 при α = 0,95.
при α = 0,95.
Контрольные вопросы
1. Что называется абсолютной погрешностью прямых измерений?
2. Что называется относительной погрешностью?
3. Как определить среднее арифметическое значение и среднее квадратичное отклонение случайной величины?
4. Нормальный закон распределения значений случайной величины и его основные свойства.
5. Что называется доверительной вероятностью и доверительным интервалом? Как они между собой связаны?
6. Определение погрешности прямых измерений методом Стьюдента.
7. Расчет погрешности косвенных измерений.
Лабораторная работа № 2
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДОГО ТЕЛА
Цель работы - ознакомиться с методом обработки результатов измерений, определить плотность тела.
Приборы и принадлежности: цилиндр, плотность которого требуется измерить, штангенциркуль, микрометр, аналитические весы (при необходимости).
Введение
Плотность вещества характеризует распределение массы по объему тела. При равномерном распределении массы по объему (однородное тело) плотность

где т – масса тела, V – его объем, d и h – диаметр и высота цилиндра, которые измеряются с помощью штангенциркуля.
В данной лабораторной работе определяется плотность ма-
териала ρ, из которого изготовлены цилиндры.
Расчеты завершаются определением величины доверительного интервала для плотности при заданной надежности
(α = 0,95) по правилам вычисления погрешности косвенных измерений.
Порядок выполнения работы
Задание I. Измерение диаметра цилиндра
1. Измерьте 5–7 раз диаметр цилиндра d с помощью микрометра. Результаты измерений занесите в табл. 1.
2. Найдите среднее арифметическое значение диаметра по формуле
 |
,
где п – число измерений, i – номер измерения.
3. Вычислите отклонения результатов отдельных измерений
от среднего арифметического  и квадрата отклонения
и квадрата отклонения 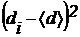 . Занесите результаты в табл. 1.
. Занесите результаты в табл. 1.
Таблица 1
Микрометр №... Цена деления микрометра Δ= 0,01 мм, погрешность прибор δ = 0,01 мм.
| № п/п | 
| 
| 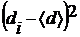
|
| … | |||
| Σ | - | ||
| среднее | - | - |
4. Найдите полуширину доверительного интервала Δ d по формуле
 |
где τ (α, n) – коэффициент Стьюдента для заданной доверительной вероятности (чаще всего выбирают α = 0,95; таблица коэффициентов Стьюдента приведена в приложении II), п–- количество измерений, δ – погрешность прибора, Δ – цена деления шкалы прибора.
5. Рассчитайте относительную погрешность ε d измерения диаметра цилиндра по формуле
ε d = ( Δ d /< d >) 100%.
6. Результат измерения запишите в стандартном виде:
 мм, ε d =... при α = 0,95.
мм, ε d =... при α = 0,95.
Задание II. Измерение высоты цилиндра
Высоту цилиндра измерьте 5–7 раз с помощью штангенциркуля, данные занесите в табл. 2.
Проведите расчеты погрешности измерения высоты так же, как это было сделано в задании I.
Результат представьте в стандартном виде:
 мм, ε h =... при α= 0,95.
мм, ε h =... при α= 0,95.
Таблица 2
Штангенциркуль № ... Цена деления штангенциркуля ω = 0,1мм, погрешность прибора δ = 0,1 мм.
| № п/п | hi | hi – < h > | (hi – < h >)2 |
| … | |||
| Σ | - | ||
| среднее | - | - |
Задание III. Измерение массы цилиндра
Измерьте массу цилиндра на аналитических весах с ценой деления 1 мг. В этом случае значение массы можно определить с высокой точностью, а погрешность прибора и погрешность округления массы достаточно малы, и поэтому погрешностью в определении массы цилиндра можно пренебречь.
Задание IV. Вычисление плотности цилиндра и оценка
погрешности косвенных измерений
1. Вычислите среднее значение плотности цилиндра по формуле
 |
,
где < т >, < d >,< h >– средние значения массы, диаметра и высоты цилиндра.
Число p= 3,14159... округлите так, чтобы его относительная погрешность была на порядок (в 10 раз) меньше наибольшей из относительных погрешностей ε d,ε h,ε m. Например, если наибольшая из этих погрешностей больше 13 %, то число следует округлить до двух значащих цифр, т.е. π ≈ 3,1. В этом случае относительная погрешность
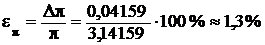 |
.
Если же наибольшая относительная погрешность ε d,ε h,ε m больше 0,5%, но меньше 13%, то число следует округлить до трех значащих цифр: π = 3,14.
При правильном выборе степени округления любой константы (например, числа π) погрешность округления не внесет существенного вклада в величину доверительного интервала измеряемой величины.
2. Рассчитайте относительную погрешность в определении плотности цилиндра по формуле
 |
.
3. Рассчитайте абсолютную погрешность определения плотности цилиндра
 .
.
Результат измерений запишите в стандартном виде:
 кг/м3,
кг/м3,  =... % при α = 0,95
=... % при α = 0,95
Контрольные вопросы.
1. Что называется плотностью вещества? Укажите размерность плотности и единицы измерения.
2. Прямые и косвенные измерения в данной лабораторной работе.
3. Получите формулы для расчета плотности твердых тел в форме шара и параллелепипеда.
Лабораторная работа № 3






