Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).

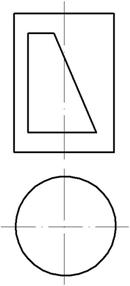
Рис. 147
Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис.148)
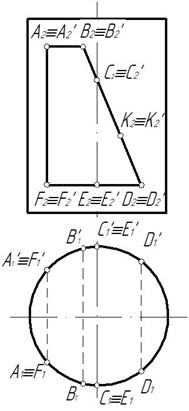
Рис. 148
Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции,а ось x 23 через профильную ось симметрии.
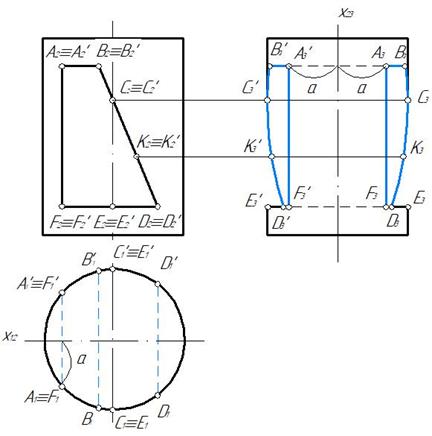
Рис.149
Пример 2. Построить три проекции конуса с вырезом (рис. 150).

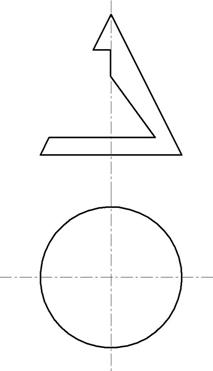
Рис. 150
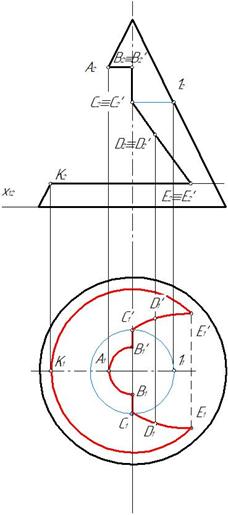
Рис. 151
Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).
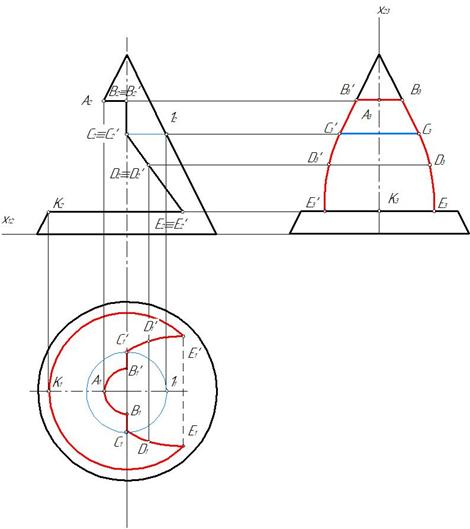
Рис. 152
На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции, а ось x 23 через профильную ось симметрии.
Пример 3. Построить три проекции вырезе на призме (рис. 153).
Рис. 153
Решение показано на рис. 154
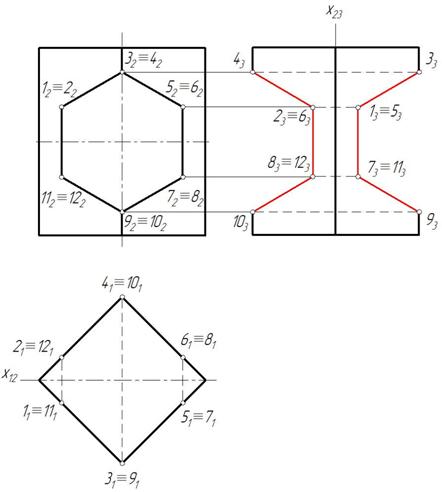
Рис. 154
Пример 4. Построить три проекции выреза на пирамиде (рис. 155).
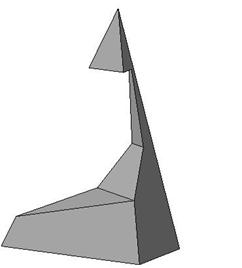
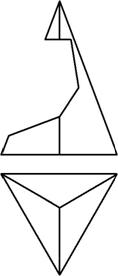
Рис. 155
Отмечаем фронтальные проекции характерных точек выреза – это точки 12, 22, 32, 42, 52, 62. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А1В1С1. На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).
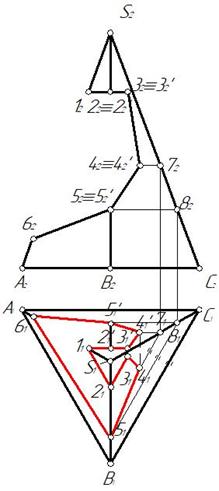
Рис. 156
Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.
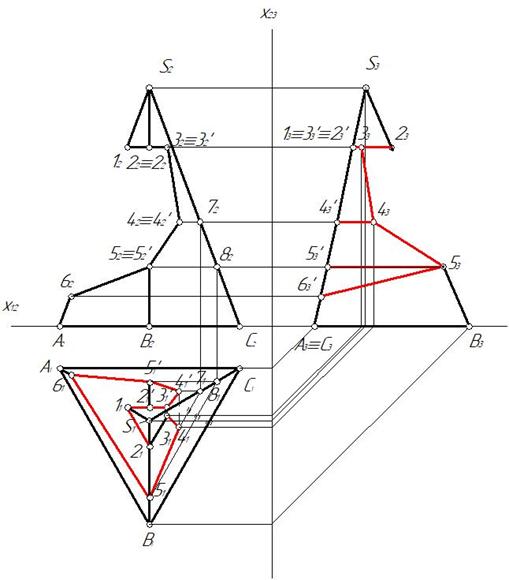
Рис. 157
Пример 5. Построить три проекции выреза на сфере (рис. 158).
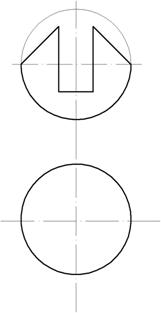
Рис. 158
Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).
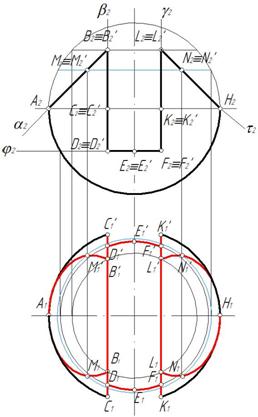
Рис. 159
Построение профильной проекции показано на рис. 160
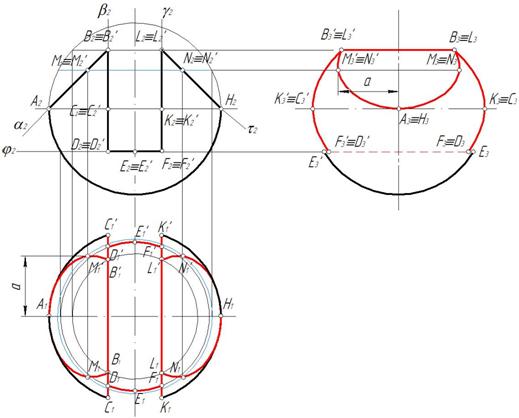
Рис. 160
Метрические задачи






