В общем случае указанная задача решается следующим образом. Через заданную прямую проводят вспомогательную плоскость и строят линию пересечения вспомогательной плоскости с поверхностью геометрического тела. Точки пересечения этих двух линий являются искомыми точками пересечения.
Пример 1. Построить точки пересечения прямой l с пирамидой. Определить видимость прямой (рис. 108).
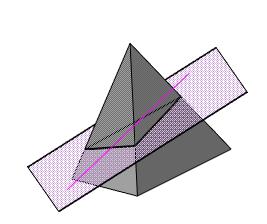

Рис. 108
Через прямую l проводим фронтально-проецирующую плоскость α^П 2, l2 ≡ α 2. Строим линию пересечения плоскости α с поверхностью пирамиды. На фронтальной проекции отмечаем 12, 22, 32, в которых α2 пересекает проекции ребер. В проекционной связи строим 11, 21 и 31 . Соединяем горизонтальные проекции 11, 21, 31 ломаной линией с учетом видимости. На горизонтальной плоскости проекций все грани пирамиды видимы. Следовательно, треугольник 11-21-31 видимый (рис. 109). На пересечении горизонтальной проекции l 1 с горизонтальной проекцией 11-21-31 отмечаем горизонтальные проекции M 1 и N 1 точек М и N. Строим фронтальные проекции M 2 и N 2 на l 2.


Рис. 109 Рис. 110
Определяем видимость прямой l. Между полученными точками M и N на обеих проекциях прямая невидима всегда. Горизонтальная проекция l 1 невидима только между M 1 N 1. На плоскости П 2: точка М находится на видимой грани ASB, следовательно, М 2 видима и фронтальная проекция l 2 видима до М 2. Точка N принадлежит грани А SC, невидимой относительно П2. Следовательно, фронтальная проекция N 2 невидима и фронтальная проекция l 2 от N 2 до ребра S 2 C 2 невидима (рис. 110).
Пример 2. Построить точки пересечения прямой l с конусом. Определить видимость прямой (рис. 111).
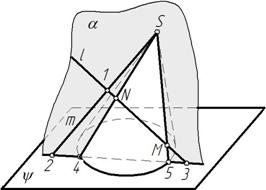

Рис. 111
Для определения точек пересечения прямой с конусом целесообразно через прямую l провести плоскость, проходящую через вершину конуса S, которая пересечет поверхность конуса по образующим. Зададим плоскость α двумя пересекающимися прямыми m и l. Для определения образующих S 4 и S 5, по которым плоскость α пересекает поверхность конуса, построена линия 2–3 пересечения плоскости α с плоскостью основания конуса. На пересечении α1 с основанием конуса отмечаем 41 и 51 точек 4 и 5 (рис.112).


Рис. 112 Рис. 113
Горизонтальные проекции образующих S141 и S151 пересекаются с горизонтальной проекцией l1 в точках М1 и N1 , а затем по линиям связи отмечаем проекции М2 и N2 точек М и N.
Для определения видимости достаточно установить видимость точек пересечения ее с поверхностью. Видимость точек определена по видимости образующих, проходящих через них. Точка N 2 не видима, так как принадлежит невидимой образующей относительно П 2, следовательно, прямая l 2 невидима до очерковой образующей. Точки M 1 и N 1 видимы, так как находятся на видимых относительно П 1 образующих. Между полученными точками M и N прямая не видима на обеих проекциях. За очерком поверхности прямая видима всегда (рис. 113).
Пример 3. Построить точки пересечения прямой l со сферой. Определить видимость прямой (рис. 114).


Рис. 114
Через прямую проводим вспомогательную плоскость так, чтобы линия пересечения поверхности сферы с плоскостью была простой геометрической формы – окружность. Рационально провести горизонтальную плоскость α, l 2 ≡ α 2 (рис. 115). Плоскость α пересекает поверхность сферы по окружности радиуса R.


Рис. 115 Рис. 116
На пересечении горизонтальной проекции l 1 и окружности радиуса R отмечаем искомые горизонтальные проекции M 1 и N 1. Фронтальные проекции M 2 и N 2 строим на фронтальной проекции l 2 прямой l.
Определяем видимость прямой l. Между полученными точками M и N прямая всегда невидима на обеих проекциях. Точки M 2 и N 2 находятся выше экватора, значит горизонтальные проекции M 1 и N 1 видимы. Горизонтальная проекция прямой l 1 видима (невидима только от M 1 до N 1). Фронтальная проекция l 2 до М2 видима, так как точка М лежит на видимой части сферы относительно плоскости проекций П 2. Точка N лежит на невидимой части сферы относительно плоскости проекций П 2, следовательно, фронтальная проекция l 2 от N 2 до очерка сферы невидима. За очерком сферы прямая l всегда видима (рис. 116).
Пример 4. Построить точки пересечения прямой l со сферой. Определить видимость прямой (рис. 117).

Рис. 117
Проводим через прямую l вспомогательную горизонтально-проецирующую плоскость α. Плоскость пересекает поверхность сферы по окружности, которая на плоскость П 2 спроецируется в эллипс. Чтобы не строить эллипс, воспользуемся методом дополнительного проецирования на плоскость П 4 – горизонтально-проецирующую и параллельную прямой l. Тогда линия пересечения спроецируется на П4 в окружность радиуса R.


Рис. 118 Рис. 119
Строим дополнительную проекцию прямой АВ на плоскость П 4 (рис. 118). На пересечении отмечаем дополнительные проекции точек М4 и N 4 . Затем строим горизонтальную и фронтальную проекции точек М и N. Видимость прямой l установлена по видимости точек М и N. Точка М расположена выше экватора сферы, т. е. на видимой относительно П 1 половине сферы, а точка N – ниже экватора, т. е. на невидимой половине. Поэтому относительно П 1 точка N – видима, а точка M – невидима (закрыта в скобки). Относительно П2 точки М и N видимы, поскольку находятся перед главным меридианом сферы (рис. 119).
Пересечение поверхностей
Для построения линии пересечения двух поверхностей нужно найти ряд точек, общих для обеих поверхностей, и соединить полученные точки в определенной последовательности с учетом видимости.
Характер линии пересечения поверхностей зависит от формы поверхностей и их взаимного расположения. В общем случае линией персечения может быть:
а) пространственная ломаная линия – при пересечении многогранников
б) пространственная кривая – при пересечении двух кривых поверхностей или состоящая из отрезков плоских кривых при пересечении кривой поверхности и многогранника.
В некоторых случаях линия пересечения может быть плоской кривой –окружностью, эллипсом.
1.18.1. Пересечение многогранников
Линия пересечения многогранников представляет собой ломаную линию, каждое звено которой является отрезком линии пересечения граней первого и второго многогранника. Общий порядок решения задачи следующий.
1. Определяем те ребра каждого многогранника, которые не пересекают граней другого. Эти ребра, очевидно, не будут участвовать в построениях.
2. Определяем точки пересечения ребер первого многогранника с гранями второго.
3. Определяем точки пересечения ребер второго многогранника с ребрами первого.
4. Соединяем найденные точки. Соединяем те точки, которые лежат на одних и тех гранях каждого из многогранников.
Пример 1. Построить линию пересечения пирамиды с призмой (рис. 120).
Из чертежа видно, что ребра M, N, E призмы не пересекают граней пирамиды, поэтому надо определять точки пересечения граней призмы с ребрами пирамиды. Пирамида полностью пронизывает призму, линия пересечения состоит из двух частей.


Рис. 120
Призма занимает горизонтально-проецирующее положение. Грань призмы NE пересекает ребра пирамиды в точках 1, 2, 3. Отмечаем горизонтальные проекции точек 11, 21, 31 на пересечении горизонтальных проекций ребер пирамиды с гранью. Затем по линии связи на соответствующих ребрах пирамиды отмечаем фронтальные проекции этих точек. Фронтальные проекции 12, 22, 32 соединяем с учетом видимости. Грани А SC и BS А видимы относительно фронтальной плоскости проекций П2, следовательно, отрезки 12-22 и 12-32 видимы. Отрезок 22-32 принадлежит невидимой грани пирамиды CSB, следовательно, он невидим. Аналогично строим точки пересечения грани призмы MN с ребрами пирамиды. Линия пересечения состоит из двух замкнутых ломаных линий. Определяем также видимость ребер пирамиды и граней призмы (рис. 121).
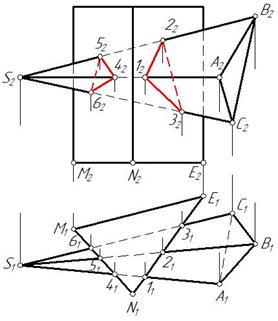
Рис. 121
1.18.2. Пересечение кривой поверхности с поверхностью многогранника
Грани многогранника, вобщем случае, пересекают кривую поверхность по плоским кривым линиям, пересекающимся между собой в точках, лежащих на ребрах многогранника.
Пример. Построить линию пересечения конуса и трехгранной призмы (рис. 122).


Рис. 122
Верхннее основание призмы пересекает поверхность конуса по окружности. Боковые грани призмы пересекаются с поверхностью конуса по гиперболам. Определим самые высокие точки гипербол. Для этого на горизонтальной проекции проводим окружность, касающуюся граней призмы и опускаем перпендикуляры, чтобы определить точки касания D 1 и Е1. Эта окружность на фронтальной плоскости проекций спроецируется как отрезок, параллельный основанию конуса.
Отметим характерные точки K и F, находящиеся на очерковых образующих конуса. Фронтальные проекции K2 и F 2 будут определять границы видимости линий пересечения на гранях АС и ВС (рис. 123).


Рис. 123 Рис. 124
Для нахождения промежуточных точек гипербол строим еще окружность и отмечаемм точки 11, 21, 31, 4 1, 5 1, 6 1. Фронтальные проекции этих точек определяем по линии связи на фронтальной проекции этой окружности. Полученные точки соединяем плвавной кривой с учетом видимости. Фронтальная проекция гиперболы на грани АВ невидима, так как грань АВ невидима относительно плоскости проекций П2 (рис. 124). Определяем также видимость очерков.
1.18.3. Пересечение кривых поверхностей
Кривые поверхности пересекаются в общем случае по пространственной кривой линии, проекции которой строятся обычно по точкам.
Пример 1. Построить линию пересечения цилиндра и усеченного конуса (рис. 125).


Рис. 125
Две кривые поверхности пересекаются по пространственной кривой.
Цилиндрическая поверхность является фронтально-проецирующей. Следовательно, фронтальная проекция линии пересечения совпадает с фронтальным очерком цилиндра – окружностью. Построим горизонтальную проекцию, исходя из условия принадлежности точек этой линии, поверхности усеченного конуса. Отмечаем характерные точки – фронтальные проекции точек А2 и Т2 на пересечении фронтальных очерков цилиндра и усеченного конуса (рис. 126).


Рис. 126 Рис. 127
Отметим фронтальные проекции M 2, N 2,в которых будет меняться видимость линии пересечения на горизонтальной плоскости проекций. Точки K 2, L 2 – низшие точки линии пересечения. Точки D 2, E 2, G 2, H 2 – точки изменения видимости на профильной плоскости проекций. В2, С2 – выбраны произвольно на фронтальном очерке цилиндра.
Горизонтальные проекции точек, принадлежащих поверхности усеченного конуса, находим на окружностях соответствующего радиуса. Соединяем полученные точки плавной линией с учетом видимости. Точки, принадлежащие видимой части поверхности цилиндра относительно горизонтальной плоскости проекций, соединяем сплошной линией. В точках М1, N 1 происходит изменение видимости. Определяем видимость горизонтальных и фронтальных очерков цилиндра, и усеченного конуса (рис. 127).
Пример 2. Построить линию пересечения тора с цилиндром (рис. 128).


Рис. 128
Цилиндр занимает горизонтально-проецирующее положение. Горизонтальная проекция линии пересечения совпадает с горизонтальным очерком цилиндра.


Рис. 129 Рис. 130
Фронтальную проекцию линии пересечения находим как линию, принадлежащую тору. Точки А2 и В2 отмечаем на пересечении фронтальных очерков тора и цилиндра (рис. 129).
Для нахождения фронтальной проекции С 2 проводим по поверхности тора линию а (а1, а2), которая на фронтальную плоскость проекций спроецируется в виде дуги окружности радиуса R. На этой дуге отмечаем фронтальную проекцию С2 и D 2 (проекция точки D, находящаяся на невидимой части цилиндра). Затем найдем произвольные точки М, N, E, F. Для этого строим на поверхности тора линию b. Фронтальная проекция b 2 – дуга окружности радиуса R 1 . Полученные точки соединяем плавной линией (рис. 130). Определяем видимость очерков поверхностей.
Пример 3. Построить линию пересечения сферы с конусом (рис. 131).
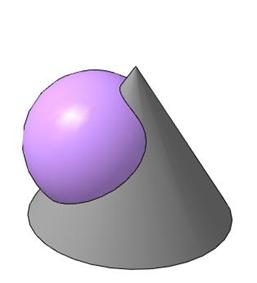

Рис. 131
Заданы две поверхности общего вида. У этих поверхностей имеется общая плоскость симметрии, поэтому линия пересечения будет симметрична относительно этой плоскости. Обе поверхности второго порядка, следовательно, линия их пересечения пространственная кривая четвертого порядка.
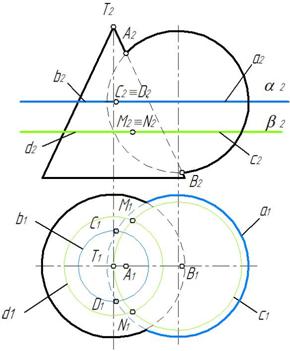

Рис. 132 Рис. 133
Отметим характерные точки линии пересечения. Точки А и В лежат на пересечении фронтальных очерков. Точки С и D находим на пересечении экватора сферы a и окружности b поверхности конуса, лежащих в одной горизонтальной плоскости α. Аналогично находим и другие точки линии пересечения. Так точки М и N строим как пересечение окружностей c и d, принадлежащих одной горизонтальной плоскости β (рис. 132).
Полученные точки соединяем плавной кривой с учетом видимости. При установлении видимости следует помнить, что эта линия будет видима, если она принадлежит как поверхности сферы, так и конуса. Точки А и В отделяют видимую относительно фронтальной плоскости часть линии пересечения (она проходит через точки А, С, М, В) от невидимой. В данной задаче фронтальные проекции видимой и невидимой части линии пересечения совпадают.
Точки С и D отделяют видимую относительно горизонтальной плоскости часть линии пересечения от невидимой. Точка А видима относительно горизонтальной плоскости проекций, так как лежит выше экватора сферы. Следовательно, линия, проходящая через точки А, С, D – видима, остальная часть линии невидима. Определяем видимость очерков поверхности конуса и сферы (рис. 133).






