Способы задания плоскости представлены в табл. 5.
Таблица 5
| Способ задания | Наглядное изображение | Эпюр |
| Три точки, не лежащие на одной прямой | 
| 
|
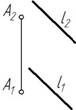
| Прямой и точкой, не лежащей на этой прямой | 
| 
|
| Двумя пересекающимися прямыми | 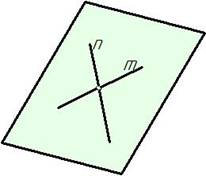
| 
|
| Двумя параллельными прямыми | 
| 
|
| Любой плоской фигурой | 
| 
|
Плоскости бывают общего и частного положения (рис. 27)

Рис. 27
Если плоскость не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения. Примеры чертежа плоскости общего положения показаны в табл. 5.
Плоскости частного положения
Плоскостями частного положения называются плоскости параллельные или перпендикулярные плоскостям проекций.
1.8.1. Проецирующие плоскости
Если плоскость перпендикулярна только одной плоскости проекций, то она называется проецирующей (табл. 6).
Таблица 6
| Наименование плоскости | Наглядное изображение | Эпюр |
| Горизонтально- проецирующая Δ АВС ^П 1 | 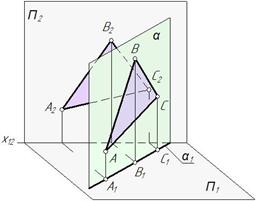
| 
|
| Фронтально-проецирующая Δ АВС ^П 2 | 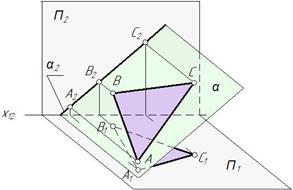
| 
|
| Профильно-проецирующая Δ АВС ^П 3 | 
| 
|
1.8.2. Плоскости уровня
Если плоскость перпендикулярна одновременно двум плоскостям проекций, а, следовательно, параллельна третьей, то она называется плоскостью уровня (табл. 7).
Таблица 7
| Наименование плоскости | Наглядное изображение | Эпюр |
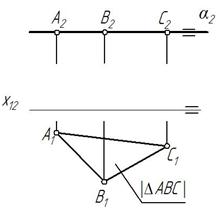
| Горизонтальная Δ АВС ‖П 1 | 
| 
|
| Фронтальная Δ АВС ‖П 2 | 
| 
|
| Профильная Δ АВС ‖ П 3 | 
| 
|
│Δ АВС │ – натуральная (истинная) величина Δ АВС.
Пример. Определить положение плоскостей в пространстве. В каждой плоскости построить точку (рис. 28).

Рис. 28
Плоскость α (a ‖ b) называется горизонтальной. Фронтальная проекция А2 точки А, принадлежащей плоскости, находится на фронтальной проекции плоскости, а горизонтальная А 1 по линии связи может быть отмечена в любом месте (рис. 29).
Плоскость β называется фронтально-проецирующей. Фронтальная проекция В2 точки В находится на фронтальной проекции плоскости β 2, а горизонтальная В1 на линии связи может быть отмечена в любом месте.
Плоскость γ(Δ АВС) называется фронтальной. Горизонтальная проекция М1 точки М, принадлежащей этой плоскости, находится на горизонтальной проекции плоскости А1 В1С1. Фронтальную проекцию М2 отмечаем по линии связи в любом месте.
Плоскость ω называется горизонтально-проецирующей. Построение точки N, принадлежащей этой плоскости, показано на рис. 29.

α‖П1 β^П2 γ‖П2 ω^П1
Рис. 29
Наглядное изображение плоскостей и точек показано на рис. 30.

Рис. 30






