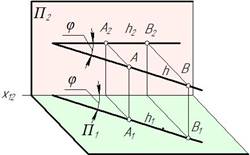
Как отмечалось выше, две проекции геометрической фигуры на эпюре однозначно определяют эту фигуру в пространстве. Однако в ряде случаев при решении задач бывает необходимо или целесообразно строить дополнительные проекции. При этом выбор аппарата дополнительного проецирования определяется условием конкретной задачи.
Дополнительную ортогональную проекцию строят на плоскости, перпендикулярной к одной или двум плоскостям проекций.
Плоскость дополнительных проекций, перпендикулярную плоскостям П 1 и П 2 обозначают П 3 и называют профильной плоскостью проекций (рис. 9, а). А3 – профильная проекция точки А.
а) б) в)

Рис. 9
Для получения эпюра плоскость П 1 повернем вокруг оси х12, плоскость П 3 вокруг оси х23 до совмещения с фронтальной плоскостью П 2 (рис. 9, б). На рис. 9, в построена дополнительная ортогональная проекция точки А на эпюре. Расстояние от оси х23 до профильной проекции А 3 равно расстоянию от оси х12 до точки А1.
На рис. 10 точка А ортогонально спроецирована на плоскости П 1 и П 2, а также на плоскость П 4, перпендикулярную к П 1.
Линия пересечения плоскостей П 1 и П 4 – ось х14. Для получения эпюра плоскость П 4 поворачивают вокруг оси х14 до совмещения с плоскостью П 1. Так как точка А не изменяет своего положения относительно плоскостей П 1 и П 2, то расстояние от точки А до плоскости П 1 остается неизменным.
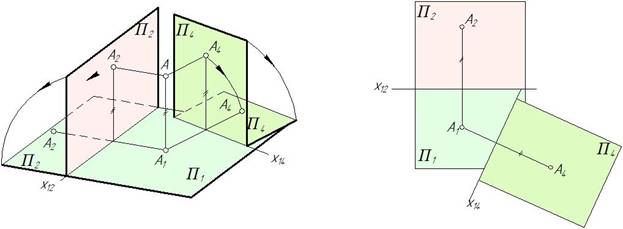
Рис. 10
Для построения на эпюре дополнительной ортогональной проекции точки А на плоскости П 4, перпендикулярной П 1 (рис. 10), нужно через А1 провести линию связи, перпендикулярную к оси х14, и отложить на ней от оси х14 расстояние от точки А2 до оси х12.

Рис. 11
Четверти пространства
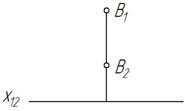
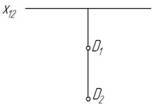
Две взаимно перпендикулярные плоскости П 2 и П 1 делят пространство на четыре двугранных угла, называемых четвертями пространства или квадрантами. В табл. 2 показан порядок отсчета четвертей. А также показаны точки, расположенные в различных четвертях пространства.
Таблица 2
| Четверть | Наглядное изображение | Эпюр |
| 1 | 
| 
|
| 2 | 
| 
|
| 3 | 
| 
|
| 4 | 
| 
|
На рис. 12 показаны одновременно все четыре точки, расположенные в различных частях пространства.

Рис. 12
Если точка располагается на плоскости, то одна из ее проекций находится на оси х 12. Точка N находится на оси х 12, проекции этой точки совпадают с самой точкой (рис. 13).

Рис. 13
Проекции прямой
Из геометрии известна аксиома: через две точки можно провести одну и только одну прямую. Следовательно, прямая на эпюре определяется проекциями двух точек.
Прямые линии могут занимать по отношению к плоскостям проекций различные положения (рис. 14).

Рис. 14
1.4.1. Прямые общего положения
Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения (рис. 15).

Рис. 15
Прямая общего положения не проецируется в натуральную величину ни на одну из плоскостей проекций.
1.4.2. Прямые уровня
Прямые, параллельные какой-либо плоскости проекций, называются прямыми уровня (табл. 3).
Таблица 3
| Наименование прямой | Наглядное изображение | Эпюр | |
| Горизонтальная (горизонталь) АВ ‖П 1 |
| 
| |
| Фронтальная (фронталь) АВ ‖П 2 | 
|
| |
| Профильная АВ ‖П 3 | 
|
| |
где│АВ│ – натуральная или истинная величина отрезка.
1.4.3. Проецирующие прямые
Прямые, перпендикулярные плоскостям проекций, называются проецирующими (табл. 4).
Таблица 4
| Наименование прямой | Наглядное изображение | Эпюр |
| Горизонтально-проецирующая АВ ^П 1 | 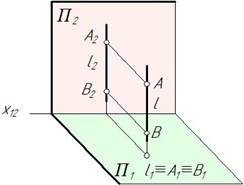
| 
|
| Фронтально-проецирующая АВ ^П 2 | 
| 
|
| Профильно-проецирующая АВ ^П 3 | 
| 
|
Проецирующие прямые параллельны двум плоскостям проекций. На эти плоскости проекций они проецируются в натуральную величину.