1. Установить погрешность.
2. Построить график, чтобы найти отрезки, содержащие по одному корню или по одному экстремуму (см. Работу 2_2. Решение уравнения).
2.1. Заполнить Таблицу 1 значениями a, b, n и формулой для 
(рис. 13). Создать имена для ячеек.
2.2. Заполнить Таблицу 2 числами от 0 до n; формулами для координаты 
и значениями полинома P (x) по формуле своего варианта.
2.3. Сделать условное форматирование так, чтобы увидеть, в каких точках полином меняет знак. Откорректировать границы a и b.
2.4. Построить график с помощью точечной диаграммы без маркеров.
3. Найти корни двумя способами.
Первый способ: при помощи инструмента Подбор параметра, заполнив Таблицу Корни — 1 способ.
Создать имя для столбца x0, ввести в него определенные по графику приближенные значения корней. В столбец под заголовком P(x0) скопировать формулу полинома из Таблицы 2, заменить аргумент x на x0. Уточнить значение каждого корня при помощи инструмента Подбор параметра, как делали в Работе 2_2. Решение уравнения.
Второй способ: при помощи надстройки Поиск решения, заполнив Таблицу Корни — 2 способ.
1) Создать имена для каждой ячейки столбца x0 — x1_, x2_, x3_, — ввести в него определенные по графику приближенные значения корней. В столбец под заголовком P(x0) скопировать формулу полинома из Таблицы 2, заменяя аргумент x на x1_, x2_, x3_ соответственно. Создать имена ячеек столбца P(x0) — P1_, P2_, P3_.
2) Уточнить первый корень: найти значение переменной x, при котором значение полинома P (x) будет равно нулю. Целевая функция — это P (x), а ограничения — это границы отрезка, содержащего корень. Выделить ячейку P1_ и открыть окно «Параметры поиска решения». Заполнить строки (рис. 14), добавить ограничения. Нажать кнопку «Найти решение» и получить первый корень.
3) Найти следующий корень. В окне «Параметры поиска решения» заменить
– целевую функцию теперь это P2_;
– имя ячейки с корнем x1_ на x2_;
– неравенства, которые теперь должны задавать отрезок, содержащий другой корень (с помощью кнопки «Изменить»)
Рис. 14. Окна инструмента Поиск решения и Добавление ограничения
– Нажать кнопку «Найти решение» и получить новый корень.
Повторяя эти действия найти остальные корни.
4. Найти максимум.
4.1. Заполнить Таблицу «Максимум» аналогично таблицам «Корни», задавая имена xmax и Pmax ячейкам, содержащим аргумент x и полином P (x), соответственно.
4.2. Выделить ячейку Pmax и открыть окно «Параметры поиска решения». Изменить строки (рис. 15), поменять ограничения с помощью кнопки Изменить. Нажать кнопку «Найти решение» и получить координаты точки максимума.
Рис. 15. Поиск максимума с помощью инструмента Поиск решения
5. Найти минимум. Сделать аналогичную Таблицу «Минимум». В окне «Параметры поиска решения» заменить целевую функцию, слово max на min в графе «До» и ограничения задающие отрезок. Получить координаты точки минимума.
6. Отформатировать таблицы и график.
7. Продолжить Отчет 2. Графика и исследование функций. Часть 4. Исследование полинома.
7.1. В разделе 1. Задание написать задание с формулой полинома для своего варианта.
7.2. В разделе 2. Результаты под подзаголовком Excel описать сходства и различия средств «Подбор параметра» и «Поиск решения». Прояснить необходимость графика при работе с надстройкой «Поиск решения».
7.3. Результаты работ, выполненных в Excelэкспортировать в Word.
ВАРИАНТЫ
| 1. | 
| 2. | 
|
| 3. | 
| 4. |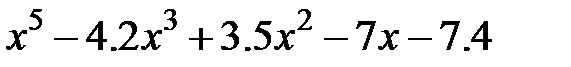 
|
| 5. | 
| 6. |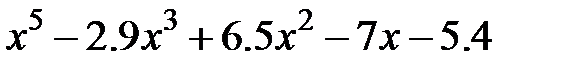 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
| 15. | 
| 16. | 
|
