- тақырып
- мақсаты
- тапсырмалар
- әдістемелік нұсқаулар
- негізгі схемалар, формулалар
- сұрақтар
9. Студенттердің өзіндік жұмысына арналған материалдар: үйге берілген тапсырмалардың мәтіні, әр бір тақырып бойынша өзін-өзі тексеру материалдары, реферат т.б. ұй жұмыстары бойынша тапсырмалар, әдебиет тізімі және арналған уақыт көлемі.
- үй тапсырмаларының мәтіндері,
- әр-бір тақырып бойынша өзі-өзі бақылау үшін материалдары,
- реферат тақырыптары
- кейстер
- кроссвордтар
- есептер шығару
- жаттығулар
Студенттердің өзіндік жұмыс тапсырмалары.
Бақылау жұмысы №1
Тақырыбы: «Ықтималдықтар теориясының негізгі ұғымдары».
Мақсаты: Ықтималдықтың классикалық анықтамасының формуласына ерекше көңіл аударыңдар, өйткені ықтималдық теориясының көп есептерін шығарғанда кілті болып есептеледі. Сонымен қатар комбинаторика формулаларымен еркін қолдана білу қажет, салыстырмалы жиілігі, геометриялық және гипергеометриялық ықтималдық ұғымдарын білу.
Тапсырма: Мына тақырыптарға есептер шығару:
1. Ықтималдықтың классикалық анықтамасы
2. Салыстырмалы жиілігі
3. Гипергеометриялық үлестірім
4. Геометриялық ықтималдықтар.
| Тапсырма | Балл | |
| Ықтималдықтар теориясының негізгі ұғымдары | 1-2 | |
| Барлығы: |
Нұсқа №1
1. Урнаға 1-ден 20-ға дейін нөмірленген 20 шар салынған.Алынған шардың нөмері 37 болуының ықтималдығын тап.
2. Бүлінген жерлері бар картоптың түйнектеррінің пайда болуының салыстырмалы жиілігі 0,15. Карзинкеде 350 картоптың түйнегі бар. Қанша картоптың түйнегі бүлінген болады?
3. Студент бағдарламаның 25 сұрағының 20-сына жауабын біледі. Емтихан алушының қойған 3 сұрағына жауабын білетінің ықтималдығын табу.
4. Радиусы R-ға тең дөңгелек ішіне нүкте лақтырылған.Дөңгелекке іштей сызылған дұрыс алтыбұрыштың ішінде нүкте болатынының ықтималдығын тап. Нүктенің дөңгелек бөлігінің ішіне түсу ықтималдығы осы бөліктің ауданына пропорционал және оның дөңгелек арқылы орналасуына тәуелді емес.
Нұсқа №2
1. Бір уақытта екі ойын сүйектерін лақтырғанда.Ұпай қосындысы 5-ке тең болуының ықтималдығы қандай
2. Бидай тұқымының өнгіштігі 90% екені белгілі. 360 өсімдіктер шығу үшін қанша дән алу керек.
3. Оқу залында ықтималдықтар теориясы бойынша 6 оқулық бар, оның 3 жұмсақ қапты.
Кітапханашы 2 оқулық алды. Оқулықтың екеуі жұмсақ қапты болатынының ықтималдығын тап.
4.Радиусы R-ға тең дөңгелек ішіне нүкте лақтырылған. Дөңгелекке іштей сызылған дұрыс үшыбұрыштың ішінде нүкте болатынының ықтималдығын тап. Нүктенің дөңгелек бөлігінің ішіне түсу ықтималдығы осы бөліктің ауданына пропорционал және оның дөңгелек арқылы орналасуына тәуелді емес.
Нұсқа №3
1. Жәшікте 50 бірдей детальдар бар, олардың 5 боялған. Алынған детальдың боялған болуының ықтималдығы қандай.
2. Қарудан атқанда көздеген жерге тиюінің салыстырмалы жиілігі 0,85. Егер 120 оқ атылған
болса, тиген оқтың санын тап.
3. Жәшікте 20 электр шамы бар, оның 6 стандартты емес Алынған 5 шамның ішінен 3 стандартты емес екенінің ықтималдығын тап.
4. Радиусы R-ға тең дөңгелек ішіне нүкте лақтырылған. Дөңгелекке іштей сызылған дұрыс шаршының ішінде нүкте болатының ықтималдығын тап. Нүктенің дөңгелек бөлігінің ішіне түсу ықтималдығы осы бөліктің ауданына пропорционал және оның дөңгелек арқылы орналасуына тәуелді емес.
Нұсқа №4
1. Ойын сүйек лақтырылды. Жұп ұпай саны түсетін ықтималдығы қандай.
2. Бидай тұқымының өнгіштігі 90℅ 200 өсімдік шығу үшін, қанша дән алу керек.
3. Топта 12 студент бар, оның 8 оқу озаты.Тізім бойынша 9 студент тандалған. Тандалған студенттердің арасында 5 оқу озаты болатындығының ықтималдығын тап.
4. Радиусы R-ге тең дөңгелектің ішінде нүкте алынған.Осы нүкте дөңгелектің центрінен r (r< R) кем аралықта болатындығының ықтималдығын тап.
Әдебиеттер: 3,6,7,12,14,18,23
Бақылау жұмысы №2
Тақырыбы: «Ықтималдықтарды көбейту және қосу теоремалары. Толық ықтималдық формуласы, Бейес формуласы».
Сабақтың мақсаты: A+B, A B, оқиғаларын айыра білу, шығарғанда ықтималдықтарды қосу және көбейту теоремаларын білу, толық ықтималдық формуласы, Бейес формуласы қолданылуын айыра білу.
Тапсырма: Мына тақырыптарға есептер шығару:
1.Ықтималдықтарды қосу теоремалары
2. Ықтималдықтарды көбейту теоремалары.
3. Толық ықтималдық формуласы
4. Бейес формуласы
| Тапсырма | Балл | |
| Ықтималдықтарды көбейту және қосу теоремалары. Толық ықтималдық формуласы, Бейес формуласы | ||
| Барлығы: |
Нұсқа №1
1. Көздеген жерге оқ тию ықтималдығы р=0,9 3 рет атқанда 3 оқ тиетінінің ықтималдығын тап.
2. Үш мерген нысанаға оқ атады. Бірінші мерген көздеген жерге оқ тию ықтималдығы 0,6 тең, екіншісінікі-0,7, үшінсінікі-0,8. Бір оқ ату нәтижесінде
а) бір мерген
б) барлық үш мерген
в) мергеннің ең болмаса біреуі
көздеген жерге тиетінің ықтималдығын тап.
3.№1 зауытта дайындалған жәшікте 12 деталь бар. № 2 зауытта дайындалған 20 деталь және
№3 зауытта дайындалған 18 деталь бар №1зауытта дайындалған детальдың сапалылығының жоғарғы ықтималдығы 0,9-ға тең, №2 зауытта жасалған детальдың жоғарғы сапалылығының ықтималдығы 0,6. №3 зауытта жасалған детальдың жоғарғы сапалылығының ықтималдығы 0,9-ға тең. Алынған детальдың жоғарғы сапалы болатындығынының ықтималдығын тап.
Нұсқа №2
1. Бірінші жәшікте бірінші сортты деталь 30%, екіншісінде 40%. Әр жәшіктен бір-бір детальдан
алынады.Алынған детальдың екеуіде бірінші сортты болатындығының ықтималдығын анықта.
2. Құрылғы бір-бірінен тәуелсіз жұмыс істейтін үш элементтен тұрады. Бірінші, екінші және үшінші
элементтердің жұмыс істейтіндігінің ықтималдығы (t уақытында) сәйкесінше 0,6; 0,7; 0,8 тең. t
уақытының ішінде тоқтаусыз жұмыс істейтін
а) тек бір элемент
б) тек ғана екі элемент.
в) ең болмаса бір элемент
болатынының ықтималдығын тап.
3. Ауруханаға орташа алғанда 50% К ауруымен, 30% L ауруымен, 20% М ауруымен науқастар түседі. К ауыруының толық емделетінінің ықтималдығы 0,7, ал L және М ауруларына бұл ықтималдықтар сәйкесінше 0,8 және 0,9 тең. Ауруханаға түскен науқас ауруханадан дені сау болып шығады. Осы науқас К ауруымен сырқаттанғанының ықтималдығын тап.
Нұсқа №3
1. Мерген бір атқанда 10 ұпай алатынының ықтималдығы 0,1-ге тең. 9 ұпай алатынының ықтималдығы –0,3-ке тең. 8 әлде одан кем ұпай алатынының ықтималдығы –0,6 тең.
Мерген бір атқанда 9 ұпайдан кем емес алатынының ықтималдығын тап.
2. Құрылғы тәуелсіз жұмыс істейтін үш элементтен тұрады. Бірінші, екінші және үшінші элементтердің тоқтаусыз жұмыс істейтін ықтималдығы сәйкесінше 0,7; 0,8; және
0,9 тең. t уақытының ішінде тоқтаусыз жұмыс істейтін
а) тек бір элемент.
б) барлық үш элемент.
в) ең болмаса бір элемент.
болатынының ықтималдығын тап.
3. Бидай егуге дайындалған бірінші сортты тұқым 40%, екінші сорт –50%, үшінші сорт-10% Бірінші сортты астықтың өнімділігінің ықтималдығы 0,8, екінші сорттың- 0,5, үшінші сорттың-0,3. Жорамалдап алған астығы шығатынының ықтималдығын тап.
Нұсқа №4
1.Үш мерген нысанаға атады. Бірінші мерген нысанаға атқандағы тиюінің ықтималдығы 0,6, екіншісі - 0,7, үшіншісі- 0,8. Бір атқаннан барлық үшеуінің нысанаға дәл тиетінің ықтималдығын тап.
2. Апат болатын туралы дабыл беретін сигнализацияға
екі сигнализатор орнатылған Бірінші сигнализаторға апатқа ұшырағанда жұмыс істейтіндігінің ықтималдығы 0,95-ке тең.
Екінші сигнализатор үшін –0,9. Апатқа ұшырағанда
а) тек қана бір сигнализатор
б) екі сигнализатор
в) ең болмаса бір сигнализатор
жұмыс істейтіндігінің ықтималдығын тап.
3. Бензоколонка тұратын тас жолмен өтіп бара жатқан жүк машиналар санының жеңіл машина санына қатынасы 3/2-ге тең. Жүкті машинаның жанармай қүйдыртатының ықтималдығы 0,1, жеңіл машинаға бұл ықтималдық-0,2-ге тең. Бензоколонкаға жанармай қүйдыртуға машина келді. Осы жүк машина екенінің ықтималдығын тап.
Әдебиеттер: 3,6,7,12,14,18,23
Бақылау жұмысы №3
Тақырыбы: «Тәуелсіз тәжірибелер. Бернулли формуласы».
Лапластың локальдық және интегральдық теоремасы».
Сабақтың мақсаты: «тәжірибелерді қайталау», «үйлесімсіз тәжірибелер» ұғымдарын меңгеру, осы тақырыпқа арналған есептердің шығару жолдарын жеңіл қылатын Бернулли формуласының қорытындылауын талдау.
Тапсырма: Есептер шығару
1. Бернулли формуласы.
2. Пуассон формуласы.
3. Лапластың локальдық теоремасы.
4. Лапластың интегральдық теоремасы.
| Тапсырма | Балл | |
| Тәуелсіз тәжірибелер. Бернулли формуласы». Лапластың локальдық және интегральдық теоремасы. | 1, 2 | |
| Барлығы: |
Нұсқа №1
Нұсқа
1. Берілген өсімдіктің дәнінің өнгіштігі 90% құрайды. Төрт отырғызған дәннен
а) үш,
б) үштен кем емес көктейтіндігінің ықтималдығын тап.
2. Тұқымның 0,1% арамшөп. 2000 тұқымды кездейсоқ іріктегенде 5 тұқым арамшөп
болатынының ықтималдығы қандай.
3. Трактор зауытында жұмысшы алмасуға дейін 400 деталь шығарады. Деталь бірінші сортты болатын ықтималдығы 0,8-ге тең. Бірінші сортты деталь 330 дана болатын ықтималдығы қандай
4. А оқиғасының әрқайсысында 150 тәуелсіз тәжірибелер бар екенінің ықтималдығы р=0,6 берілді. Осы тәжірибелерде А оқиғасы 78 кем емес және 96 артық емес шығатынының ықтималдығын тап.
Нұсқа №2
1. Мақтада ұзын талшықтың саны 80% құрайды. 5 алған талшықтың ішінде ұзын
а) үшеу
б) екеуден артық емес
болатынының ықтималдығы қандай
2. Детальдардың бүлінген болып шығатынының ықтималдығы 0,008. 500 кездейсоқ іріктеп алған детальдардың ішінде үшеуі бүлінген болатынының ықтималдығын тап
3. Трактор зауытында жұмысшы алмасуға дейін 400 деталь дайындайды. Деталь бірінші сортты болатын қтималдығы 0,9-ға тең. Бірінші сортты деталь 372 дана болатынының ықтималдығын тап.
4. Әрбір 100 тәуелсіз тәжірибесінде А оқиғасының көріну ықтималдығы р=0,8. Осы тәжірибелерде А оқиғасы 72 кем емес және 84 артық емес көрінетінінің ықтималдығын тап.
Нұсқа №3
1. Бір суатта тұқы 80% құрайды. Суаттан аулаған балықтың 5-інің
а) 4 тұқы
б) 4 кем емес тұқы
болатынының ықтималдығын тап.
2. Құрылғы бір-бірінен тәуелсіз жұмыс істейтін 1000 элементтен тұрады. Бір сағат ішінде оның кез келгенінің тоқтап қалу ықтималдығы 0,002-ге тең. Бір сағат ішінде 4 элемент тоқтап қалатынының ықтималдығын тап.
3. Трактор зауытында жұмысшы алмасуға дейін 300 деталь шығарады. Деталь бірінші сортты болатынының ықтималдығы 0,75. Бірінші сортты деталь 240 дана болатынының ықтималдығы қандай.
4. А оқиғасының әрқайсысында 400 тәуелсіз тәжірибелер бар екенінің ықтималдығы р=0,9 берілді. Осы тәжірибелерде А оқиғасы 345 кем емес және 372 артық емес шығатынының ықтималдығын тап.
Нұсқа №4
1. Аспап 4 түйінен тұрады. Алмасуға дейін әр түйінің тоқтаусыз жұмыс істеу ықтималдығы 0,8-ге тең.Түйіндер бір-бірінен тәуелсіз саптан шығады. Бір алмасудың ішінде
а) екі түйін
б) екі түйінен кем емес
шығатындығынының ықтималдығын тап.
2. Радиоактивтік сәулелеуден кейін бактериялардың тірілу ықтималдығы 0,004-ке тең. Сәулелеуден кейін 500 бактериядан 3 қалатындығының ықтималдығын тап.
3. Трактор зауытында жұмысшы алмасуға дейін 600 деталь дайындайды. Деталь бірінші сортты болатын ықтималдығы 0,6-ға тең. Деталь бірінші сортты 375 дана болатынының ықтималдығын тап.
4. А оқиғасының әрбір 600 тәуелсіз тәжірибесінде көріну ықтималдығы р=0,4.Осы тәжірибелерде А оқиғасы 210 кем емес 252 артық емес көрінетінінің ықтималдығын тап.
Әдебиеттер: 3,6,7,12,14,18,23
Бақылау жұмысы №4
Тақырыбы: «Кездейсоқ шамалар. Кездейсоқ шамалардың үлестірім заңдары».
Сабақтың мақсаты: Кездейсоқ шамалар ұғымын қайталау, дискретті және үздіксіз шамаларды айыра білу, әр түрлі заңдарымен олардың үлестірімімен танысу.
Тапсырма: Мына тақырыптарға есептер шығару:
1. Дискретті кездейсоқ шамалардың үлестірім заңдары.
2. Үзіліссіз кездейсоқ шамалардың сандық сипаттамалары.
3. Ықтималдықтың үлестірім функциясы, үлестірім тығыздығы
| Тапсырма | Балл | |
| Кездейсоқ шамалар. Кездейсоқ шамалардың үлестірім заңдары | ||
| Барлығы: |
Нұсқа №1
1. Х дискреттік кездейсоқ шаманың үлестірім заңы берілді. Табу керек:
1) М(х) математикалық үмітін
2) Д(х) дисперсиясын
3) σ орташа квадраттық ауытқуын.
| х | ||||
| У | 0,3 | 0,2 | 0,4 | 0,1 |
2. Х кездейсоқ шамасы F(х) интегралдық үлестірім
функциясы арқылы берілді. Табыңдар:
1) f(х) дифференциалдық үлестірім функциясын
(үлестірім тығыздығын)
2) М(х) математикалық үмітін
3) Д(х) дисперсиясын
f(х)= 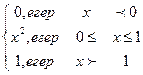
3. Х үзіліссіз кездейсоқ шаманың (0;π/2) интервалында үлестірім тығыздығы f(х)=Сsin3х, интервалдан тыс f(х)=0. С параметрін тап.
Нұсқа №2
1. Х дискреттік кездейсоқ шаманың үлестірім заңы берілді. Табу керек:
1) М(х) математикалық үмітін
2) Д(х) дисперсиясын
3) σ орташа квадраттық ауытқуын
| Х | ||||
| р | 0,2 | 0,4 | 0,3 | 0,1 |
2. Х кездейсоқ шамасы F(х) интегралдық үлестірім функциясы арқылы берілді.
Табыңдар:
1) f(х) дифференциалдық үлестірім тығыздығын.
2) М(х) математикалық үмітін
3) Д(х) дисперсиясын
F(х)= 
3. Х дискреттік кездейсоқ үлестірім заңы бойынша берілген.
| Х | |||
| Р | 0,5 | 0,4 | 0,1 |
Осы шаманың үлестірім функциясының графигін салыңдар.
Нұсқа №3
1. Х дискреттік кездейсоқ шаманың үлестірім заңы берілді. Табу керек:
1) М(х) математикалық үмітін
2) Д (х) дисперсиясын
3) σ орташа квадраттық ауытқуын.
| х | ||||
| р | 0,2 | 0,2 | 0,5 | 0,1 |
2. Х кездейсоқ шамасы F (х) интегралдық үлестірім
функциясы арқылы берілді.
Табу керек:
1) f(х) дифференциалдық үлестірім тығыздығын(үлестірім тығыздығын);
2) М (х) математикалық үмітін;
3) Д (х) дисперсиясын.
F(х)= 
3. Х үзіліссіз кездейсоқ шамасының (0;1) интервалында үлестірім тығыздығы f(х)=С arctgХ, осы интервалдан тыс f(х)=0. С параметрін тап.
Нұсқа №4
1. Х дискреттік кездейсоқ шаманың үлестірім заңы берілді. Табу керек:
1) М(х) математикалық үмітін
2) Д(х) дисперсиясын
3) σ орташа квадраттық ауытқуын.
| х | ||||
| р | 0,1 | 0,5 | 0,3 | 0,1 |
2. Х кездейсоқ шамасы F(х) интегралдық үлестірім функциясы арқылы берілді. Табыңдар:
1) f(х) дифференциалдық үлестірім тығыздығын.
(үлестірім тығыздығын)
2) М(х) математикалық үмітін
3) Д(х) дисперсиясын
F(х)= 
3. Х дискреттік кездейсоқ шамасы үлестірім заңы бойынша берілген
| х | |||
| р | 0,5 | 0,3 | 0,2 |
Осы шаманың үлестірім функциясының графигін салыңдар.
Әдебиеттер: 3,6,7,12,14,18,23
Жеке тапсырма №1
Тақырыбы: «М атематикалық статистика пәні.
Таңдамалы әдіс ».
Сабақтың мақсаты: Вариациалық қатардың сандық сипаттамалары анықтау, есептің қорытындысы бойынша дұрыс талдау және қорытындылай білу.
Тапсырма: Вариациалық қатардың берілгендері бойынша барлық оның сандық сипаттамаларын табыңдар және графигін салыңдар (полигон, гистограмма, кумулята, огива)
| Тапсырма: | Балл | |
| Вариациалық қатардың сандық сипаттамалары (дискретті белгісі) | Вариациалық қатардың сандық сипаттамаларын табыңыз (жай арифметиалық орта, өлшенген арифметиалық орта, дисперсия, орта сызықтық ауытқу, орта квадраттық ауытқу, мода, медиана) | |
| Табыңыз: бастапқы және орталық моменттер, вариация, ассиметрия коэффициенттерін және эксцесс. Қорытындылар. | ||
| Графиктерін салыңыз – полигон, гистограмма, кумулята, огива. | ||
| Барлығы: |
Вариант№1
Вариант№2
Вариант№3
Вариант№4
Вариант№5
Вариант№6
Вариант№7
| -4 | |||||||||
| -3 | |||||||||
| -3 | -6 | ||||||||
| -7 | |||||||||
| -1 |
Вариант№8
Вариант№9
Вариант№10
Вариант№11
Вариант№12
Вариант№13
Вариант№14
Вариант№15
Вариант№16
Әдебиеттер: 3,6,7,12,14,16,17
10.Оқу, өндірістік және дипломалды сараманды өткізу жөнінде әдістемелік нұсқаулар және есеп құжаттарының түрі (егер пән бойынша қажет болса).
11.Студенттің оқу жетістіктерін бақылау және бағалау материалдары (бақылау тапсырмалары, тесттік тапсырма, өзін-өзі даярлау сұрақтар тізімі, емтихандық билеттер және т.б.)
- білімді бағалау схемасы
- білімді бағалау саясаты
- письменные контрольные задания
- тестовые задания
- перечень вопросов для самоподготовки
- экзаменационные билеты Ықтималдықтар теориясы және математикалық статистикадан
тест тапсырмалары мен сұрақтары
| № п.п | Қиындық деңгейі | Сұрақтар | Тарау Тақырып | А) (Дұрыс жауап) | В) | С) | D) | Е) |
| Қандай оқиға ақиқат деп аталады? | Міндетті түрде орындалатын оқиға. | Қолайлы жағдайлар дың болуына қарамастан орындалмайтын оқиғаларды | Пайда болуыда мүмкін, пайда болмауыда мүмкін | Тәжірибе нәтижесі… | Кез келген нәтиже | |||
| Қандай оқиға мүмкін емес деп аталады? | Қолайлы жағдайлар дың болуына қарамастан орындалмайтын оқиғаларды | Міндетті түрде орындалатын оқиға. | Пайда болуыда мүмкін, пайда болмауыда мүмкін | Тәжірибе нәтижесі… | Кез келген нәтиже | |||
| Қандай оқиға кездейсоқ деп аталады | Тәжірибе нәтижесінде пайда болуыда мүмкін, пайда болмауыда мүмкін. | Қолайлы жағдайлар дың болуына қарамастан орындалмайтын оқиғаларды. | Міндетті түрде орындалатын оқиға. | Тәжірибе нәтижесі… | Кез келген нәтиже | |||
| Ықтималдықтың классикалық анықтамасының формуласын: | Р(А)=m/n | W(A)=m/n | A 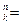 
| C  = = 
| P  =n!. =n!.
| |||
| Салыстырмалы жиілігі есептелетін формуланы көрсетіңіз: | W(A)=m/n | Р(А)=m/n | A 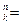 
| C  = = 
| P  =n!. =n!.
| |||
| Мынадай жағдайда m/n, қатынасы оқиғаның ықтималдығы деп аталады: | m – оқиғаға септесетін жағдайлар саны, n – барлық мүмкін жағдайлар саны | m – барлық мүмкін жағдайлар саны,n- оқиғаға септесетін жағдайлар саны | n –оқиғаға шақыратын жағдайлар саны да, m - барлық жағдайлар саны | m –оқиғаға шақыратын жағдайлар саны да, n - барлық мүмкін жағдайлар саны | m,n – оқиғаға қатысты кез-келген жағдайлар саны | |||
| Ақиқат оқиғаның ықтималдығы тең: | 
| 0,1 | ||||||
| Мүмкін емес оқиғаның ықтималдығы тең: | 
| 0,1 | ||||||
| Кездейсоқ оқиғанын ықтималдығы Р(А) теңсіздікті қанағаттандырады…: | 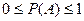
|  . .
| 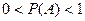 . .
|  . .
|  . .
| |||
| n элементтен жасалатын алмастыру есептелетін формуласын табыңдар: | P  =n!. =n!.
| A 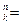 
| C  = = 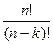
| C 
| P  =n =n
| |||
| n элементтен k-дан алынған орналастыру есептелетін формуласын табыңдар: | A 
| C  = = 
| C 
| P  =n!. =n!.
| A 
| |||
| n элементтен k-дан жасалған терулер есептелетін формуласын табыңдар: | 
| A 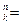 
| C  = = 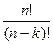
| C 
| P  =n!. =n!.
| |||
| 3 элементтен жасалатын барлық алмастырудың саны тең (Дәл анықтамаға ең жуығын көрсетіңіз) | ||||||||
| 4 элементтен жасалатын барлық алмастырудың саны тең (Дәл анықтамаға ең жуығын көрсетіңіз) | 24. | 48. | 64. | 256. | 120. | |||
| 5 элементтен жасалатын барлық алмастырудың саны тең (Дәл анықтамаға ең жуығын көрсетіңіз) | ||||||||
| 1,2,3, сандардан қанша үш таңбалы сан құрастыруға болады, егер әр цифра санның бейнелуіне бір рет кездесетін болса. | ||||||||
| 5 элементтен 2-ден жасалатын барлық орналастырудың саны тең: | ||||||||
| 6 элементтен 3-ден жасалатын барлық орналастырудың саны тең: | ||||||||
| 6 элементтен 5-ден жасалатын барлық орналастырудың саны тең: | ||||||||
| 1,2,3,4,5, сандардан қайталаусыз қанша үш таңбалы сан құрастыруға болады | ||||||||
| Әр түрлі түсті 6 жалаудан екі-екіден алынған қанша белгі құрастыруға болады: | ||||||||
| 7 элементтен 3-тен жасалатын барлық терудің саны тең: | ||||||||
| 100 элементтен 98-ден жасалатын барлық терудің саны тең: | ||||||||
| Құмырада 6 гүл болса, үш-үштен алынған гүлден неше тәсілмен гүлшоғын жасауға болады. | ||||||||
| 10 бөлшек бар жәшіктен неше тәсілмен 2 бөлшектен алуға болады. | ||||||||
| Телефон номерін теріп жатқанда абонент бір цифра ұмытып қалады, және оны кездейсоқ тереді. Керек цифраны тергенінің ықтималдығын тап. | 1/10 | 1/2 | 1/5 | |||||
| Ойын “сүйегі” (кубигі) лақтырылды. Жұп ұпай саны түсетінің ықтималдығы қандай. | 0,5 | 0,4 | 0,2 | |||||
| Ойын “сүйегі” (кубигі) 1 рет лақтырылады. 6-ға тең ұпай саны түсетінің ықтималдығы қандай? | 1/6 | 1/2 | 1/3 | 1/4 | ||||
| Ойын “сүйегі” (кубигі) 1 рет лақтырылады. 3-ке еселі ұпай саны түсетінің ықтималдығы қандай. | 1/3 | 1/2 | 1/6 | 1/4 | ||||
| Ойын “сүйегі” (кубигі) 1 рет лақтырылды. Түсетін ұпайлар саны 5 –тен кем болатынының ықтималдығын тап. | 2/3 | 1/3 | 1/2 | |||||
| Ойын “сүйегі” (кубигі) 1 рет лақтырылды. Түсетін ұпайлар саны 2 –ден артық болатынының ықтималдығын тап. | 2/3 | 1/3 | 1/2 | |||||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Ұпайлар саны ойын сүйектерінде бірдей болатынының ықтималдығын тап. | 1/6 | 1/2 | 1/36 | 5/6 | ||||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Ұпайлар саны бірінші ойын сүйегінде екінші ойын сүйегіне қарағанда артық болатындығының ықтималдығын тап. | 5/12 | 1/6 | 1/36 | 2/3 | 1/3 | |||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Ұпайлардың қосындысы жұп болатындығының ықтималдығын тап. | 1/2 | 1/3 | 1/6 | 1/4 | ||||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Ұпайлардың қосындысы 2-ден артық болатындығының ықтималдығын тап. | 35/36 | 1/6 | 1/2 | 1/3 | 1/4 | |||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Ұпайлардың қосындысы 5-тен кем болатындығының ықтималдығын тап | 5/6 | 1/6 | 1/2 | 1/3 | 1/4 | |||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Ең болмаса бір ойын сүйегінде 6 цифрасы шығатындығының ықтималдығын тап: | 11/36 | 5/36 | 12/36 | 1/4 | 1/3 | |||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Ұпайлардың көбейтіндісі 6-ға тең болатындығының ықтималдығын тап: | 1/9 | 1/4 | 1/6 | 1/3 | ||||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Түсетін ұпайлардың қосындысы 7-ге тең болатындығының ықтималдығын тап: | 1/6 | 1/36 | 1/2 | 1/3 | ||||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Түсетін ұпайлардың қосындысы 8-ге, ал айырмасы 4-ке тең болатындығының ықтималдығын тап | 1/18 | 1/6 | 1/2 | 1/36 | ||||
| Екі ойын “сүйегі” (кубигі) лақтырылады. Түсетін ұпайлардың қосындысы 5-ке, ал көбейтіндісі 4-ке тең болатындығының ықтималдығын тап: | 1/18 | 1/36 | 1/6 | 1/2 | 1/3 | |||
| 100 бөлшегі бар ұйымнан техникалық бақылау бөлімі 5стандартты емес бөлшек тапқан.Стандартты емес бөлшектердің шығуының салыстырмалы ықтималдығын тап. | 0,05 | 0,03 | 0,01 | 0,5 | 0,6 | |||
| Нысанаға 35 оқ атылды. 21 оқ тию белгіленген. Нысананың жеңілуінің салыстырмалы жиілігі неге тең? | 21/35 | 35/21 | 15/21 | 52/8 | 3/35 | |||
| Нысанаға 20 оқ атылды. 18 оқ тию белгіленген. Нысананың жеңілуінің салыстырмалы жиілігі неге тең? | 0,9 | 20/18 | 0,3 | 0,36 | ||||
| Құрылғылар ұйымын зерттеуде жарамды құрылғылардың салыстырмалы жиілігі 0,9-ға тең болатындығы белгілі болды. Егер барлығы 200 құрылғы жасақталған болса, жарамды құрылғылардың санын табыңыз. | 200/9 | 0,36 | 0,8 | |||||
| Бидай тұқымының өнгіштігі 90% екені белгілі. 360 өсімдіктер шығу үшін қанша дән алу керек. | ||||||||
| Қарудан атқанда көздеген жерге тиюінің салыстырмалы жиілігі 0,85. Егер 120 оқ атылған болса, тиген оқтың санын тап. | 0,85 | |||||||
| Бидай тұқымының өнгіштігі 90℅. 200 өсімдік шығу үшін, қанша дән алу керек | 222,2 | |||||||
| Урнаға 1-ден 20-ға дейін нөмірленген 20 шар салынған. Алынған шардың нөмері 37 болуының ықтималдығын тап. | ||||||||
| Ойын “сүйегі” (кубигі) 2 рет лақтырылды. Көрінген ұпайлар қосындысының 10 –нан кем болмауының ықтималдығы қандай? | 1/6 | 1/10 | 1/5 | 1/8 | 1/4 | |||
| Урнада 12 шар бар: 3 ақ, 4 қара, 5 қызыл. Урнадан қара шар алып шығатынының ықтималдығы қандай? | 1/3 | 1/4 | 1/5 | 1/2 | ||||
| Жәшіктен 1-ден бастап 100-ге дейін нөмерленген жетондар суырылған. Бірінші алынған жетонның нөмірінің ішінде 5 цифрасы болмайтындығының ықтималдығын тап: | 0,81 | 0,8 | 0,2 | 0,15 | 0,35 | |||
Қаптың ішінде 5 бірдей кубиктер бар. Әр кубиктің барлық жағында мына әріптердің біреуі жазылған:
о, п, р, с, т. Бір сызық бойында жатқан ж
Дата добавления: 2017-03-12; Мы поможем в написании ваших работ!; просмотров: 1623 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.015 с.






