Жай
Лшенген
Вариациялық коэффициенті CV – кездейсоқ шаманың тұрақсыздығының салыстырмалы көрсеткіші, процент есебімен беріледі,
CV= 
100% формуласымен есептеледі.
Вариациялық қатардың сипаттамаларына мода және медиана жатады.
Мода (МО) дискретті Х кездейсоқ шамасының модасы деп оның жиілігінің ең үлкен мәнін айтады. Егер Х үзіліссіз кездейсоқ шама болса, онда оны мына формуламен табады.
МО=хМО+h 
,
мұндағы
хМО – модальдық интервалдың бастамасы, яғни интервалға сәйкес келетін ең үлкен жиілік.
mМО – модальдық интервалдың жиілігі
mМО-1 – модальдық интервалдың алдындағы интервалдың жиілігі.
mМО+1 – модальдық интервалдан кейінгі интервалдың жиілігі.
h – топтау қадамы ( топтау қадамының интервалы)
Медиана (МЕ) Х дискреттік кездейсоқ шамасының медианасы деп, оның вариациялық қатарының ортасына келетін мәнін айтамыз. Егер n=2i – 1 (тақ сан болса), х1, х2, …, хi, хi+1, хn қатардың медианасы МЕ= хi n=2i (жұп саны болса) х1, х2, …, хi, хi+1, хn қатардың ортасына хi және хi+1. мәндері келеді. Бұл жағдайда
МЕ= 
Интервалдық вариациялық қатардың медианасы мына формуламен анықталады.
МЕ=хМЕ+h 
хМЕ – медиандық интервалдың бастамасы
mжин – ден кіші не оған тең жинақталған жиілік медианалық интервалдағы жиілік
mМЕ – медианалық интервалдағы жинақталған локалдық жиілік
h – интервалдық қадам(топтау интервалының шамасы)
Жоғарыда қарастырылған сандық сипаттамалармен бірге вариациалық моменті деген вариациалық қатардың жалпы сипаттамалары қарастырылады.
хi кездейсоқ шамасының қандай да бір А санынан ауытқуының к-дәрежесінің орта мәнін к-ретті момент деп атайды.
Мк= 
немесе Мк= 
А-ның мәндерінің таңдауына байланысты бастапқы және орталық моменттер болады. Егер тұрақты А=0, онда момент бастапқы деп аталады. Егер А=х0, мұндағы х0 – қандай да еркімізше алынған шама, онда момент х-ке қатысты бастапқы момент деп аталады.
А=0 шығады:
Егер К=0 М0=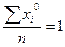 
М0= 
- нольдік ретті бастапқы моменттер.
Егер К=1 М1=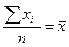 
М1=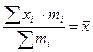 
- бірінші ретті бастапқы моменттер.
Егер К=2 М2=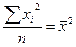 
М2= 
- екінші ретті бастапқы моменттер.
Егер К=3 М3= 
М3= 
- үшінші ретті бастапқы моменттер.
Егер К=4 М4= 
М4= 
- төртінші ретті бастапқы моменттер т.б
Практикада төртінші ретті моменттен артық қолданбайды.
Сөйтіп қандай да еркімізше алынған шамаларға қатысты сәйкесінші ретті, бастапқы моменттер қолданылады.
Мк= 
х0 қатысты бастапқы моменттер:
нольдік ретті: М0= 
бірінші ретті: М1= 
екінші ретті: М2= 
үшінші ретті: М3=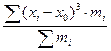 
төртінші ретті: М4= 
т.б
Егер тұрақты А шамасының орнына 
шамасының орта мәнің қойсақ, онда моменттер орталық деп аталады.
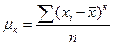
немесе
А= , егер К=0
немесе
-
нөльдік ретті орталық моменттер.
К=1
немесе
-
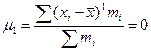бірінші ретті орталық моменттер.
К=2
немесе
-
екінші ретті орталық моменттер.
К=3
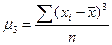
немесе
-
үшінші ретті орталық моменттер.
К=4
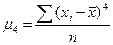
немесе
-
төртінші ретті орталық моменттер.
Үшінші ретті орталық моменттің 
орта квадраттық ауытқудың 
үшінші дәрежесіне қатынасын асимметрия коэффициенті деп аталады.
ЕС эксцесс депүш бірлікке кеміткен төртінші ретті орталық моменттің 
орта квадраттық ауытқудың төртінші дәрежесіне 
қатынасын атайды.
Қарапайым қалыпты Гаусс қисығы: ЕС=0, егер ол сүйір бұрышты болса, немесе ол сопақтау болса, ЕС>0, және керісінше егер ЕС<0 қалыпты қисық жалпақтау (жазыңқырақ) болады.
СОӨЖ жоспары
| Апта | Тақырып атауы | Сағат көлемі | Бақылау түрі |
| Комбинаторика. Геометриялық ықтималдық. Толық ықтималдық формуласы. Бейес формуласы. | БЖ | ||
| Лапластың локалдық және интегралдық теоремалары. Пуассон формуласы. | БЖ | ||
| Үлестірім заңдары. ДКШ. | БЖ | ||
| Кездейсоқ шамалардың үлестірім функциясы және үлестірім тығыздығы | БЖ | ||
| Таңдамалы әдіс. | ЖТ | ||
| Вариациалық қатардың сандық сипаттамалары. | ЖТ | ||
| Нүктелік бағалау, ығыспайтын. Эффектілік, орнықтылық бағалаулар. Бірінші және екінші текті қателіктер. | ЖШ | ||
| Корреляция коэффициенттері. Жұптық корреляция. | ЖТ | ||
| Көпөлшемді корреляция коэффициенттері. | ЖТ | ||
| Дисперсиалық талдау. | ЖТ | ||
| Барлығы |
Әдебиет:
