- тақырып
- мақсаты
- өткізу түрі
- тапсырмалар, сұрақтар
Семинар №1.
Тақырыбы: «Ықтималдықтар теориясы. Негізгі ұғымдар, оқиғалар, олардың түрлері».
Сабақтың мақсаты: Ықтималдықтың классикалық анықтамасының формуласына ерекше көңіл аударыңдар, өйткені ықтималдық теориясының көп есептерін шығарғанда кілті болып есептеледі. Сонымен қатар комбинаторика формулаларымен теру, орналастыру, алмастыру терминдерін еркін қолдана білу қажет.
Семинар сұрақтары:
1. Ықтималдықтың классикалық анықтамасы.
2. Ықтималдықтың статистикалық анықтамасы.
3. Комбинаторика формулалары.
4. Геометриялық ықтималдық
Тапсырма:
1) Телефон номерін теріп жатқанда абонент бір цифра ұмытып қалады, және оны кездейсоқ тереді. Керек цифраны тергенінің ықтималдығын тап
Жауабы: 
.
2) Жәшікте 15 бұйымдар бар, оның 10 боялған. Жинақтаушы кездейсоқ 3-ін алады. Алынған бұйымдар боялған болатынының ықтималдығын табыңыз.
Жауабы: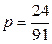 
.
3) Жәшікте 100 бұйымдар бар, оның 10 жарамсыз. Кездейсоқ 4 бұйым алынған. Алынған бұйымдардың ішінде: а) жарамсыз жоқ; б) пайдалысы жоқ екенінің ықтималдығын табыңыз.
Жауабы: а) ≈0,65
б) ≈0,00005.
4) Ойын “сүйегі” (кубигі) лақтырылды. Жұп ұпай саны түсетінінің ықтималдығы қандай.
Жауабы: 0,5.
5) Жәшіктен 1-ден бастап 100-ге дейін нөмерленген жетондар суырылған. Бірінші алынған жетонның нөмірінің ішінде 5 цифрасы болмайтындығының ықтималдығын тап:
Жауабы: 0,81.
6) Қаптың ішінде 5 бірдей кубиктер бар. Әр кубиктің барлық жағында мына әріптердің біреуі жазылған: о, п, р, с, т. Бір сызық бойында жатқан және бір-бірден алынған кубиктерден «спорт» сөзін оқып шығуға болатындығының ықтималдығын тап.
Жауабы: 
.
7) Барлық жақтары боялған куб, бірдей өлшемді 1000 кубиктерге бөлінген, олар содан соң араластырылған. Кездейсоқ алынған кубиктің боялған жақтары а) бір; б) екі; в) үш болатынының ықтималдығын табыңыз. Жауабы: а) 0,384; б) 0,096; в) 0,008.
8) 100 бөлшегі бар ұйымнан техникалық бақылау бөлімі 5стандартты емес бөлшек тапқан. Стандартты емес бөлшектердің шығуының салыстырмалы ықтималдығын тап
Жауабы: 0,05.
9) Жазықтықта радиустары сәйкесінше 5 және 10 см-ге тең екі шеңбер сызылған. Кездейсоқ үлкен доңгелекке лақтырылған нүкте шеңберлер арасындағы сақинаның ішіне түсетінің ықтималдығын табыңыз. Нүктенің жазық фигураның ішіне түсетінінің ықтималдығы фигураның ауданына пропорционал және оның орналасуына тәуелді емес.
Жауабы: 0,75.
10) Радиусы R-ға тең дөңгелек ішіне нүкте лақтырылған. Дөңгелекке іштей сызылған: а) шаршының; б) дұрыс үшбұрыштың в) дұрыс алтыбұрыштың ішінде нүкте болатынының ықтималдығын тап. Нүктенің дөңгелек бөлігінің ішіне түсу ықтималдығы осы бөліктің ауданына пропорционал және оның дөңгелек арқылы орналасуына тәуелді емес.
Әдебиеттер: 3,6,7,12,14,18,23
Семинар №2.
Тақырыбы: «Ықтималдықтарды көбейту және қосу теоремалары».
Сабақтың мақсаты: A+B, A B, оқиғаларын айыра білу, шығарғанда ықтималдықтарды қосу және көбейту теоремаларының қолданылуын айыра білу.
Семинар сұрақтары:
1.Ықтималдықтарды қосу теоремалары
2. Оқиғалардың толық тобы.
3. Шартты ықтималдық..
4. Ықтималдықтарды көбейту теоремалары.
5. Толық ықтималдық формуласы, Бейес формуласы
Тапсырма:
1) Жәшікте 4 ақ, 5 қызыл, 8 жасыл және 3 көк шарлар бар. Шарларды араластырып біреуін алып шығарады. Алынған шар боялған болатынының ықтималдығын табыңыз:
Жауабы: 
.
2) Цехта 2 тасымалдаушы жұмыс істейді. Әрқайсысының тоқтаусыз жұмыс істейтінінің ықтималдығы t уақыт ішінде 0,9-ға тең. Тасымалдаушылар бір-бірінен тәуелсіз жұмыс істейді. t уақытта
а) ең болмаса бір тасымалдаушы;
б) екеуі де;
в) ешқайсысы да емес;
г) тек қана бір тасымалдаушы тоқтаусыз жұмыс істейтінінің ықтималдығын тап:
Жауабы: а) 0,99; б) 0,81; в) 0,01; г) 0,18.
3) Құрылғы тәуелсіз жұмыс істейтін үш элементтен тұрады. Бірінші, екінші және үшінші элементтердің тоқтаусыз жұмыс істейтін ықтималдығы сәйкесінше 0,6; 0,7 және 0,8 -ге тең. t уақытының ішінде
а) тек қана бір элемент;
б) тек екі элемент;
в) барлық үшеуі де тоқтаусыз жұмыс істейтінінің ықтималдығын тап:
Жауабы: а) 0,188; б) 0,452; в) 0,336.
4) 100 лотерей билетінің ішінде 5 ұтысты. Кездейсоқ алынған 2 билеттің ұтысты болатынының ықтималдығын тап:
Жауабы: 
.
5) Екі жәшікте бөлшектер бар: біріншіде 10 (оның 3 стандартты), екіншісінде 15 (оның 6 стандартты). Әр жәшіктен кездейсоқ бір-бір бөлшектен алынады. Екеуі де стандартты болатынының ықтималдығын тап:
Жауабы: 0,12.
6) Теледидар студиясында 3 телекамера бар. Әр камера үшін берілген уақытта қосылып тұрғанының ықтималдығы 0,6-ға тең. Берілген уақытта ең болмаса біреуі ғана қосылып тұрғанының ықтималдығын тап:
Жауабы: 0,936.
7) Барлық бүйымдардың ішіндегі бірінші станоктан - 40%, екінші станоктан -30%, үшінші станоктан - 10%, төртіншіден 20% жинақтауға түскен. Бірінші станок бүйымдарының 0,1% бүлінген, екіншісінен – 0,2%, үшіншісінен - 0,25%, төртіншісінен – 0,5%. Жинақтауға түскен бүйымдардың ішінен бүлінген бүйымдардың ықтималдығын табыңыз:
Жауабы: 0,002
8) Студенттік спорт жарысына қатысуға курстың бірінші тобынан 4, екінші тобынан - 6, үшінші тобынан – 5 студент бөлінген. 1,2,3 топ студенттері институттың құрама тобына түсетінінің ықтималдығы сәйкесінше 0,9; 0,7; 0,8 –ге тең. Кездейсоқ алынған студент жарыстың қорытындысында құрамаға түсті. Студенттің құрамаға түсуінің ықтималдығын тап: Бұл студент қай тобқа кіреді:
Жауабы: 
, 
, 
.
9) Пирамидада 5 мылтықтың 3-і оптикалық көздеуімен қамтылған. Оптикалық көздеуі бар мылтықтан бір атқаннан мергеннің нысанаға тию ықтималдығы-0,95-ке; оптикалық көздеуісіз мылтықтан бұл ықтималдық-0,7-ге тең. Кездейсоқ алынған мылтықтан бір атқаннан нысанаға тию ықтималдығын тап:
10) Болт шығаратын фабрикада бірінші машина - 25%, екінші - 35%, үшінші - 40% болт шығарады. Олардың ішінде жарамсыз өнім сәйкесінше 5%, 4% және 2%. Кездейсоқ таңдалған болт жарамсыз болды. Оның үшінші машинамен шығарылғанының ықтималдығы қандай.
Жауабы: 0,875.
Әдебиеттер: 3,6,7,12,14,18,23
Семинар №3,4.
Тақырыбы: «Тәуелсіз тәжірибелер. Бернулли формуласы».
Сабақтың мақсаты: «тәжірибелерді қайталау», «үйлесімсіз тәжірибелер» ұғымдарын меңгеру, осы тақырыпқа арналған есептердің шығару жолдарын жеңіл қылатын Бернулли формуласының қорытындылауын талдау
Семинар сұрақтары:
1. Бернулли формуласы.
2. Пуассон формуласы.
Тапсырма:
1) Цехта 6 мотор бар. Әр моторға берілген уақытта оның қосулы тұрғанынының ықтималдығы 0,8-ге тең. Берілген уақытта
а) 4 мотор қосулы тұрғанының
б) барлық моторлар қосулы тұрғанының
в) барлық моторлардың сөнулі тұрғанының ықтималдығын тап
Жауабы: а) 
б) 
в) 
.
2) Екі тең қарсыластар шахмат ойнайды. Қайсы ықтималдырақ:
а) екіден бір партияны немесе төрттен екі партияны ұту;
б) төрттен екіден аз емес партия немесе бестен үштен аз болмайтындай партия ұту.
Еш қайсысының ұтпауы жауапқа алынбайды.
3) Тиын 5 рет лақтырылды. Оның жалау жағымен түсетінінің ықтималдығы:
а) екі реттен аз;
б) екі реттен аз емес.
4) Жанұяда бес бала-шаға. Осы бала-шағаның арасында
а) екеуі ұл бала да;
б) екі баладан аспайтынның;
в) екі баладан көп;
г) екіден аз емес және үштен көп емес бала болатынының ықтималдығын тап.
Бала тууының ықтималдығы 0,51 деп алынған.
5) С нүктесі AB кесіндісін 2:1 қатынаста бөліп тұр. Осы кесіндіде кездейсоқ алынған төрт нүкте берілген. Нүктелердің екеуі С нүктесінің сол жағында, қалған екеуі оң жағында орналасатынының ықтималдығын тап. Нүктенің кесіндіге түсуі кесіндінің ұзындығына пропорционал және оның орналасуына тәуелсіз емес деп алынады.
Жауабы:
.
Әдебиеттер: 3,6,7,12,14,18,23
Семинар №5.
Тақырыбы: «Лапластың л окальдық және интегральдық теоремасы».
Сабақтың мақсаты: Лапластың локальдық және интегралдық теоремаларын пайдалану жағдайларын айыруды үйрену қажет.
Семинар сұрақтары:
1) Лапластың локальдық теоремасы.
2) Лапластың интегральдық теоремасы.
Тапсырма:
1) Оқиғаның 400 тәжірибеде дәл 104 рет болатынының ықтималдығын тап, егер әр тәжірибеде оның пайда болуының ықтималдығы 0,2-ге тең болса.
Жауабы: 
.
2) Мергеннің бір атқанда нысанаға тию ықтималдығы 0,75-ке тең. 100 рет атқанда нысанаға тиетінінің ықтималдығын тап:
а) 70-тен аз және 80 –нен көп емес рет;
б) 70-тен көп емес рет.
Жауабы: а)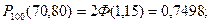 
б)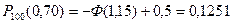 
.
3) 2100 тәуелсіз тәжірибелердің әрқайсысында оқиғаның пайда болу ықтималдығы 0,7-ге тең. Оқиғаның:
а) 1470-тен аз емес және 1500-ден көп емес рет;
б) 1470-тен аз емес рет;
в) 1469-дан көп емес рет пайда болатынының ықтималдығын тап.
4) 10000 тәуелсіз тәжірибелердің әрқайсысында оқиғаның көрінуінің ықтималдығы p=0,75. Оқиғаның көрінуінің салыстырмалы жиелігі оның абсолюттік шамасы бойынша ықтималдығынан 0,001-ден көп емес ауытқитындығының ықтималдығын тап.
Жауабы: 
.
5) Тиынды 0,6 ықтималдығымен жалау бар жағы түсетін p=0,5 ықтималдығынан абсолюттік шамасы бойынша 0,01-ден көп емес ауытқитындығын күтуге болатындай қанша рет лақтыру керек
Жауабы: n=1764.
Әдебиеттер: 3,6,7,12,14,18,23
Семинар №6.
Тақырыбы: «Кездейсоқ шамалар. Кездейсоқ шамалардың үлестірім заңдары».
Сабақтың мақсаты: Кездейсоқ шамалар ұғымын қайталау, дискретті және үздіксіз шамаларды айыра білу, әр түрлі заңдарымен олардың үлестірімімен танысу.
Семинар сұрақтары:
1. Дискретті кездейсоқ шамалар.
2. Дискретті кездейсоқ шамалардың үлестірім заңдары.
3. Дискретті кездейсоқ шамалардың сандық сипаттамалары.
Тапсырма:
1) Алты бүйымнан жасалған партияның төртеуі стандартты. Кездейсоқ үш бүйым алынған. Х таңдалған ішінен стандартты бүйымдар санының- дискретті шамасының үлестірім заңын құрастырыңыз. Үлестірім көпбұрышын салыңыз.
Жауабы:
| x | ||||
| p | 
| 
|
|
2) 1) Х дискретті кездейсоқ шаманың – тиынды екі рет лақтырғанда «герб» жағымен көріну санының биномиалдық заңын жазыңыз:
Жауабы:
| x | |||
| p |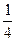 
| 
|
|
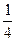
3) Құрылғы тәуелсіз жұмыс істейтін 1000 элементтен тұрады. Т уақыт ішінде тоқтаусыз жұмыс істейтінінің ықтималдығы 0,002-ге тең. Т уақыт ішінде тек қана үш элемент жұмыс істемейтінінің ықтималдығын табыңыз. Жауабы: Р1000(3)=0,18, е-2=0,13534.
4) Дүкен минералды судың 1000 шөлмегін алды. Тасымалдағанда шөлмек сынып қалатынының ықтималдығы 0.003 –ке тең. Дүкенге а)тек қана екі; б)екіден кем; в)екіден артық; г)ең болмаса бір сынық шөлмек түсетінінің ықтималдығын тап. (е-3= 0,04979):
(е-3=0,04979).
Жауабы: а)0,224; б)0,1992; в)0,5768; г)0,95.
5) Х дискретті кездейсоқ шамасы 3 мүмкін мән қабылдайды: х1=4, p1=0,5 ықтималдығымен; х2=6, p2=0,3 ықтималдығымен және х3, p3 ықтималдығымен, х3 ЖӘНЕ p3 табыңыз, егер М(х)=8:
Жауабы: х3=21,р3=0,2.
6) Х дискретті кездейсоқ шаманың мүмкін мәндерінің тізімі берілген: х1=1, х2=2, х3=3, осы шамалардың математикалық күтімі және оның квадраты белгілі: М(Х)=2,3; М(Х2)=5,9. Х-тің мүмкін мәндеріне сәйкес келетін ықтималдықтарды табыңыз.
Жауабы: р1=0,2; р2=0,3; р3=0,5
7) Егер Х және Y дисперсиялары белгілі болса Z=2X+3Y, Д(X)=4, Д(Y)=5, онда Z кездейсоқ шамасының дисперсиясын табыңыз:
Жауабы: 61.
8)Х- кездейсоқ шамасының екі тәуелсіз тәжірибелерде, егер осы оқиғалардың осы тәжірибелерде көріну ықтималдықтары бірдей және М(Х)=0,9 болса, дисперсиясын табыңыз: Жауабы: 0,495.
9) Х дискретті кездейсоқ шамасының тек екі мүмкін мәндері бар: х1 және х2, х1<х2. Х –тің қабылдайтын мәні х1–ге тең болатынының ықтималдығы 0,2-ге тең. Математикалық күтімі М(Х)=2,6 және орта квадраттық ауытқуы 
(Х)=0,8 болатынын біле отырып, үлестіру заңын табыңыз:
Жауабы:
| х | ||
| р | 0,2 | 0,8 |
10) Х дискретті кездейсоқ шамасының тек үш мүмкін мәндері бар:х1, х2 және х3, мұндағы х1 < х2 < х3,. Х –тің қабылдайтын мәндері х1 және х2 - тең болатынының ықтималдығы 0,3 және 0,2 -ге тең. Математикалық күтімі М(Х)=2,2 және дисперсиясы D(X)=0,76 екенін біле отырып, Х-тің үлестіру заңын табыңыз:
Әдебиеттер: 3,6,7,12,14,18,23
Семинар №7,8.
Тақырыбы: «Үзіліссіз кездейсоқ шамалар.
ҮКШ сандық сипаттамалары».
Сабақтың мақсаты: Кездейсоқ шамалар ұғымын қайталау, дискретті және үздіксіз шамаларды айыра білу, әр түрлі заңдарымен олардың үлестірімімен танысу.
Семинар сұрақтары:
1. Үзіліссіз кездейсоқ шамалар.
2. ҮКШ сандық сипаттамалары. Қасиеттері.
3. Ықтималдықтың үлестірім функциясы, үлестірім тығыздығы, оның
қасиеттері.
4. Қалыпты үлестірім
Тапсырма:
1) Х үзіліссіз кездейсоқ шамасының (0;2) интервалында үлестірім тығыздығы f(x)=(1/2)x, осы интервалдан тыс f(х)=0. Х шамасының математикалық күтімін тап:
Жауабы: М(Х)= 
2) Х үзіліссіз кездейсоқ шамасының (0;1) интервалында үлестірім тығыздығы f(x)=с(х2+2х), осы интервалдан тыс f(х)=0. 1) С параметрін 2) Х шамасының математикалық күтімін табыңыз:
3) Теріс емес мүмкін мәндері бар Х үзіліссіз кездейсоқ шамасы үлестірім функциясымен берілген F(x)=1-e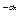 
(
>0). Х шамасының математикалық күтімін табыңыз:
4) Х үзіліссіз кездейсоқ шамасының (0;5) интервалында үлестірім тығыздығы f(x)= 
x; осы интервалдан тыс f(х)=0. Х-тің дисперсиясын табыңыз: Жауабы: D(X)= 
.
5) Үлестіру функциясымен берілген Х кездейсоқ шамасының дисперсиясын табыңыз:
F(x)= 
,
Жауабы: D(X)= .
6) Қалыпты үлестірілген Х кездейсоқ шамасының математикалық күтімі а=3 және орта квадраттық ауытқуы 2-ге тең. Х ықтималдық тығыздығын табыңыз:
7) М(Х)=3 және Д(Х)=16 екенін біле отырып, қалыпты үлестірілген Х кездейсоқ шамасының ықтималдық тығыздығын табыңыз.
8)Х кездейсоқ шамасы үлестірім функциясымен берілген F(x)= 
. Үлестірім тығыздығын f(x) табыңыз:
Жауабы: f(x)= 
9) Х кездейсоқ шамасы үлестірім тығыздығымен берілген:
f(x)=
Жауабы:F(x)=
10) Дискретті кездейсоқ шамасы үлестіру заңымен берілген
| х | ||||
| р | 0,2 | 0,1 | 0,4 | 0,3 |
Үлестіру функциясын табыңыз және оның графигін салыңыз.
11) Х үзіліссіз кездейсоқ шамасының (0; 
) интервалында үлестірім тығыздығы f(x)=C·sin2x;, осы интервалдан тыс f(х)=0. С параметрін тап:
Жауабы: С=1.
Әдебиеттер: 3,6,7,12,14,18,23
Семинар №9.
Тақырыбы: «Үлкен сандар заңы. Бернулли теоремасы».
Сабақтың мақсаты: Барлық теоремалар және Чебышев, Бернулли, Чебышев теңсіздігі үлкен сандар заңының мағынасын құрайды. Осы тақырыптың есептірінің айырмашылықтары күрделігінде, сондықтан олардың шығару жолдарын үйрену.
Семинар сұрақтары:
1. Чебышев теңсіздігі және теоремасы.
2. Үлкен сандар заңы.
3. Бернулли теоремасы.
4. Кездейсоқ функциялар.
Тапсырма:
1) Берілді: 
< 0,1,
Егер D(X)=0,01, Чебышев теңсіздігін пайдаланып, ықтималдықты бағалаңыз:
Жауабы: Р 
0,9.
2) Берілді: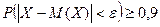 
; D(X)=0,04.
Чебышев теңсіздігін пайдаланып, 
табыңыз.
3) Жарық желісіне параллель 20 шам қосылған. Т уақыт ішінде шамның қосылатынының ықтималдығы 0,8-ге тең. Чебышев теңсіздігін пайдаланып, қосулы тұрған шамдардың саны мен Т уақыт ішінде қосулы тұрған шамдардың орта мәнінің арасындағы айырмасының абсолют шамамен алынған ықтималдығын бағалаңыз.а) 3-тен кем б) 3-тен кем емес.
Жауабы: а)0,64 б)0,36
4) Автомат бөлшектер шығарады. Математикалық күтімі бар қалыпты үлестірілген Х бөлшектердің ұзындығы бақыланады, 50 мм –ге тең. Шығарылған бөлшектердің ұзындығы 32-ден кем емес және 68-ден артық емес болады. Кездейсоқ алынған бөлшектің ұзындығы а) 50 мм-ден артық; б) 40 мм-ден кем болатынының ықтималдығын табыңыз. P(32<x<68)=1 теңдігінен табыңыз.
Жауабы: а) 0,0823; б) 0,0027.
P(32<x<68)=1 теңдігінен табыңыз.
Жауабы: а) 0,0823; б) 0,0027.
5) Х дискретті кездейсоқ шамасы үлестіру заңымен берілген:
| х | 0,3 | 0,6 |
| р | 0,2 | 0,8 |
Чебышев теңсіздігін пайдаланып, ықтималдықты бағалаңыз: < 0,2.
Бірінші М(Х) және D(X) есептеңіз.
Жауабы:0,64
6) Х дискретті кездейсоқ шамасы үлестіру заңымен берілген:
| х | 0,1 | 0,4 | 0,6 |
| р | 0,2 | 0,3 | 0,5 |
Чебышев теңсіздігін пайдаланып, ықтималдықты бағалыңыз:
Жауабы: 0,909
Әдебиеттер: 3,6,7,12,14,18,23
Семинар №10.
Тақырыбы: «М атематикалық статистика пәні.
Таңдамалы әдіс ».
Сабақтың мақсаты: Вариациалық қатардың сандық сипаттамалары анықтау, есептің қорытындысы бойынша дұрыс талдау және қорытындылай білу.
Семинар сұрақтары:
1. Бас және таңдама жиындары.
2. Вариациалық қатар және оның сандық сипаттамалары.
Тапсырма:
Вариациалық қатардың берілгендері бойынша барлық оның сандық сипаттамаларын табыңдар және графигін салыңдар (полигон, гистограмма, кумулята, огива)
Вариант№1
Вариант№2
Вариант№3
Вариант№4
Вариант№5
Әдебиеттер: 3,6,7,12,14,16,17
Семинар №11,12
